城市配送中心多目标选址模型与车辆调度仿真研究

王 永，田 铖 （重庆邮电大学 电子商务与现代物流重点实验室，重庆400065）

0 引 言

随着互联网经济浪潮的到来，网络购物等线上消费模式迅猛发展，使面向消费者的物流行业成为物流系统中的爆发点。按照十三五发展规划，物流行业作为国民经济发展的动脉和基础产业，被喻为促进经济发展的“加速器”，其发展程度成为衡量国家现代化程度和综合国力的重要标志之一。现今，电商对物流的时效性要求越来越高，而城市配送中心作为物流系统中的重要设施枢纽，承担城市主要进出港干线集散、分拣、中转等作用，并具有提升上级转运中心稳定性和缓解下级终端节点运营压力的功能。因此，城市配送中心的选址决策在物流系统中处于战略层次，合理的城市配送中心选址可以有效降低物流费用，并提升配送效率。

近年来，启发式选址算法成为国内外许多学者研究城市配送中心选址问题的有效工具。Davari 等[1]基于贪婪搜索的启发式算法，研究模糊覆盖半径的最大覆盖选址问题。Perny 等[2]通过k度中心树算法对物流配送选址进行求解。Vlachopoulou 等[3]基于现代信息技术，将城市配送中心选址问题和地理信息系统结合，并对其提出有效的解决方案。刘必争等[4]研究结合遗传算法和退火算法的城市配送中心选址，认为选址问题必须考虑车辆的巡回访问特性，并带有时间窗的限制。Contreras 等[5]针对成本不确定、需求不确定和成本需求同时不确定三种情况下的选址优化问题进行研究。Alumur 等[6]考虑数据的不精确性，研究选址决策应当考虑配送中心建设费用和需求不确定。徐小平等[7]运用改进猴群算法求解物流中心选址问题。叶一芃等[8]将物流中心选址问题构建为双层规划模型，并对该模型提出一种基于灵敏度分析的规划算法进行求解。何永贵等[9]研究基于决策者视角以及客户视角下的双层规划模型，并结合混合免疫遗传算法对物流选址进行求解。都牧等[10]构建二阶段随机规划模型，基于改进的随机分支定界算法研究有关城市物流配送问题。赵培忻等[11]将新型聚类算法和重心算法结合求解物流系统多设施选址问题，通过对比实验证明其有效性和实用性。范荣华等[12]提出一种基于直觉模糊数的配送中心选址方法，通过实例分析其选址过程。于冬梅等[13]基于设施节点损毁及不确定性需求情况下，提出一种蝙蝠优化算法求解模型。Pawel 等[14]基于实际邮政网络，研究降低运输成本的相关因素，通过图论算法求解配送中心位置。Pham 等[15]采用Fuzzy-Delphi-TOPSIS 的混合模型从候选地点确定物流中心，得出运输量、运输成本、靠近市场和客户是选择物流中心的关键因素。

基于此，本文将城市配送中心选址视为一个复杂系统，涵盖多个影响因素，综合考虑地理位置的重要性、建设规模的变化、上下级协同服务，建立多目标选址模型，设计适用于城市配送中心选址的改进多重心算法，基于DataMap 数据库的实际路网距离，对城市配送中心选址问题展开研究，并应用于“国内某大型物流企业城市配送中心选址规划”中，并在选址模型的基础上，运用Anylogic 多方法仿真软件对中心选址与车辆调度一体化的车辆运输系统开展仿真研究，能有效降低物流系统总费用，为物流企业实施城市配送中心选址策略提供了有效借鉴。

1 多目标选址模型构建

物流企业在配送网络中存在转运中心和终端节点，但转运中心通常远离核心地区，有效的配送中心选址能够提高时效和优化配送成本。城市配送中心与转运中心和终端节点构成的网络系统如图1。假定物流企业存在既定的上级转运中心、m个待建城市配送中心、φ 个可用配送车辆和n个终端节点。车辆从转运中心出发，将商品运往城市配送中心，城市配送中心需要为若干终端节点分类配送货物。为构建模型考虑如下假设：已知终端节点的数量、经纬度坐标、集货量和配送量，每个终端节点均有巡回需求。每个终端节点只能被一个城市配送中心派出的一辆车遍历，每辆车只有一条服务路线，起终点必须为同一城市配送中心，车辆动态负载量必须始终小于等于车辆的容量限制。每个城市配送中心可派出多辆车为多个终端节点服务，但终端节点的总需求量不能超过配送中心的容量限制。现要求在满足车辆承载能力的前提下，将商品送往终端节点的同时收回该点的集货商品，然后由城市配送中心将集货商品运往转运中心。

图1 城市配送中心网络系统

物流系统总费用包括三部分：城市配送中心的建设费用、转运中心↔城市配送中心的车线费用、城市配送中心↔终端节点的配送费用。其中，模型的决策变量和参数定义如下：

决策变量：

模型参数：

配送中心集合为I=｛i|i=1,2,…,m｝，终端节点集合为J=｛j|j=m+1,m+2,…,m+n｝，可用配送车辆集合为K=｛k|k=1,2,…,φ ｝，所有配送点集合为V=I∪J=｛1,2,…,m+n｝；边集合为E=｛（i,j）|i,j∈V｝，每条边对应的配送费用由i到j点的运输距离cij、单位车辆的运输费率Fν 确定；城市配送中心i的建设费用包含场地成本Oi、人工成本Pi、设备成本Di；变量θi表示区域重要度因子，通过企业决策者对每个区域进行综合评分得到，其值越大，表示该区域交通重要性越高；Ri为城市配送中心i的车线费用，表示单位商品在配送中心进行集货和分拣产生的所有费用；上级转运中心至配送中心i的距离为Li；终端节点j的配送需求为dj，集货需求为gj；车辆容量限制为Q；城市配送中心i的容量限制为Mi。

建立的数学模型表示如下：

其中：式（1） 为目标函数，表示最小化物流系统总费用，包括城市配送中心建设费用和目标函数式（2） 的费用期望值；式（2） 表示城市配送中心车线费用和配送费用之和最小；式（3）、式（4）、式（5） 保证每个终端节点有且仅有一条服务路线，且相同节点或城市配送中心之间均没有服务路线；式（6） 表示车辆运输路线的连续性；式（7） 表示服务的配送车辆总数小于可用配送车辆总数；式（8）、式（9） 表示运输车辆的容量约束；式（10） 表示每条运输路线只由一个城市配送中心服务；式（11） 表示支路约束，运输路线的总集合不包含起始点，S为车辆k服务路线的终端节点集合；式（12） 保证配送中心服务的所有终端节点需求总和不超过配送中心的容量约束；式（13）、式（14） 为决策变量的约束。

2 求解城市配送中心选址的改进多重心算法

多数量化模型只是对现实情形的简单抽象与模拟，主要依据运输距离和运输费用进行求解，没有进一步探讨物流设施的空间布局特征和物流系统的网络特性。本文提出一种新的改进多重心算法，与构建的多目标选址模型相结合，考虑与选址相关的影响因素，比如地理位置的重要程度、建设规模的变化、上下级协同服务，这样不仅提高了求解选址问题的精度，也对实际的选址研究具有借鉴意义。

2.1 算法原理与实现

重心法又称网格法或精确重心法，该方法基于物理学中对二维封闭图形求解重心的原理，将系统网络中需求节点与资源点看作某平面范围内分布的二维封闭图形，将需求量看作为物体的重量，整个系统网络的重心作为资源的最优地址[16]。传统的重心法求解中心点坐标是将运输量作为决策要素，使物流系统总费用最小化的城市配送中心地址就是最优选址点。其计算公式可以表示为：

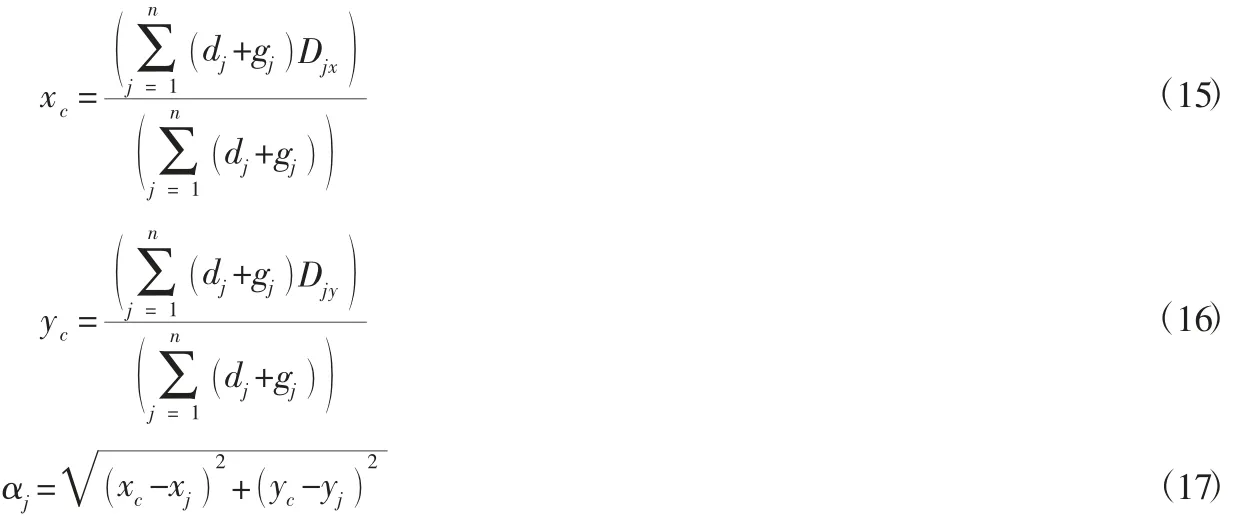
式中：（xc,yc）为待定的城市配送中心的空间坐标，（xj,yj）为配送网络中各终端节点的空间坐标，Djx对应第j个终端节点的x坐标，Djy对应第j个终端节点的y坐标，αj为城市配送中心到终端节点的直线距离。

2.2 改进多重心算法

重心法的优势是求解速度快，但是仅考虑运输成本作为唯一的决策因素，不适用于复杂网络选址。因此，提出一种改进多重心算法，利用重心法求解中心点的原理，结合影响城市配送中心选址的多方面定性因素，加入权重影响因子，以终端节点的经纬度坐标和运输量为依据，求解使物流系统总费用最小的城市配送中心选址。该方法相较于重心法，既考虑了影响配送中心选址过程中的定量因素，也考虑了多重定性因素，提升了对于异常节点的鲁棒性和算法精度。详细计算步骤如下：

Step1：选址模型的相关参数设置及初始化：建设城配中心的场地成本Oi、人工成本Pi、设备成本Di，区域重要程度因子θi，配送中心车线成本Ri，每个终端节点j的配送量和集货量为dj和gj，配送中心i到节点j的运输距离为cij，单位车辆的运输费率Fν。

Step2：通过终端节点的相关数据模拟定量计算出配送网络的重心点，即城市配送中心的初始坐标。

Step3：计算初始城市配送中心坐标至各节点坐标之间的距离，得到距离矩阵。

Step4：考虑影响城市配送中心选址的多重因素（如表1 所示），进行归一化处理，加入权重因子Wj，修正城市配送中心选址坐标。

Step5：计算目标函数值，与其他实验结果进行对比。

表1 影响城市配送中心选址的多重因素

3 算例分析——以国内某大型物流企业城市配送中心选址规划为例

通过对某大型物流企业城市配送中心规划项目的调研，城市核心区域内存在转运中心和终端节点，随着业务量的增长，下级节点屡屡出现爆仓等异常现象。因此，现计划建设城市配送中心提升上级转运中心稳定性以及缓解下级终端节点运营压力。在核心区域内建设城市配送中心符合企业发展布局，旨在以物流系统总费用最小化为目标。

根据区域内23 个终端节点数据，将覆盖节点区域分别通过重心法、K-medoids 算法和改进多重心法求解城市配送中心选址坐标，从而计算物流系统总费用。算例结果基于三种启发式算法得出可行解，相关实验结果如表2 所示。

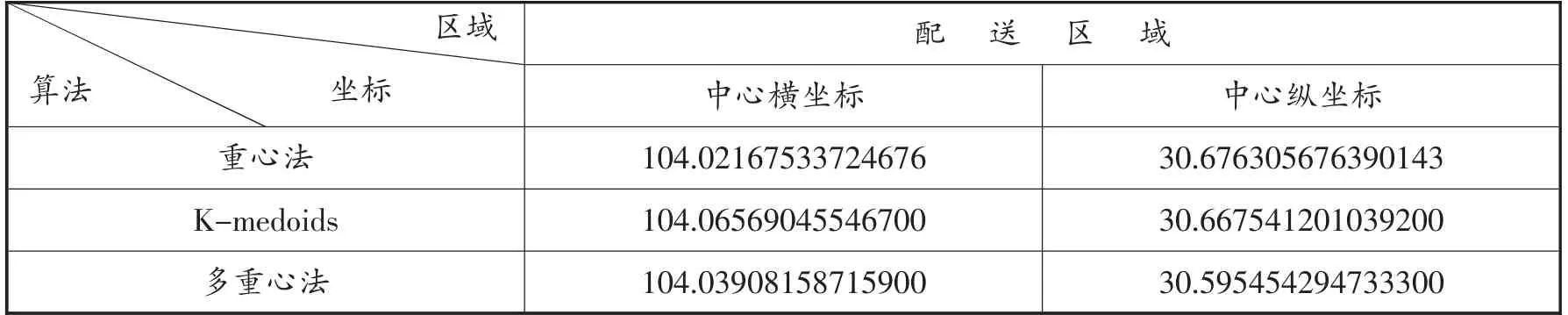
表2 算法实验结果

为了验证城市配送中心规模的不同数值对物流系统总费用的影响，根据项目调研获得的城市配送中心规模增长系数，计算城市配送中心规模的增长趋势，如表3 所示。

表3 城市配送中心规模的不同数值

根据改进的多重心算法对构建的多目标选址模型进行求解，利用上述数据进行多组实验计算，运输距离基于DataMap 数据库中各终端节点的实际路网距离，测算出物流系统总费用变化趋势，数据结果如图2 所示。

通过图2 分析可以得出：

（1） 聚类算法常用于物流选址模型，其算法思想是根据分类原则，把n个数据节点划分为k（类k≦n）s求最优聚类中心。K-medoids 聚类算法求出的城市配送中心经纬度坐标解，距离其他所有终端节点运输距离总和为最小，与传统聚类算法相比对于异常节点鲁棒性增强，但是K-medoids 算法运行的局限在于仅考虑了节点的经纬度坐标值，而没有考虑运输成本。

（2） 重心法是求解物流设施选址问题的典型方法。根据各节点之间的距离、运输量和经纬度坐标求出近似最优解。车线成本和配送成本是根据上下级之间的DataMap 路网距离和总需求量决定。但是，重心法求解过程没有具体考虑城市配送中心规模变化以及地理位置的重要性等因素。

（3） 求解城市配送中心选址的改进多重心算法是在重心法的基础上，考虑选址与实际路由规划的相互影响、选址的多层次影响特性以及城市配送中心和转运中心存运数量均衡等定性因素，对多节点城市配送中心选址求解并应用于实际选址规划研究。

图2 城市配送中心规模不同数值下物流系统总费用变化趋势

以上数据在一定程度上说明了本文算法得到的结果是优于重心法和K-medoids 算法。随着城市配送中心集货量和配送量的增加，物流系统总费用与城市配送中心规模承线性正相关，城市配送中心的建设费用是物流系统总费用增加的主要原因，而配送费用和车线费用对物流系统总费用不再敏感。

为了进一步验证本文模型和算法的有效性和可行性，在选址模型的基础上，对配送过程进行仿真，运用Anylogic 多方法仿真软件对中心选址与车辆调度一体化的车辆运输系统开展仿真研究，实验结果如图3 所示。

以选址模型和物流企业实际运作数据为基础，运用Anylogic 多方法仿真建模软件，对城市配送中心车辆调度问题进行仿真，增加时间窗约束条件，验证车辆调度系统仿真模型的有效性。车辆调度方案为：配送中心—节点2—节点19—节点21—节点20—节点15—节点9—节点10—节点17—节点8—节点6—节点11—节点14—节点13—节点22—节点18—节点3—节点5—节点16—节点1—节点7—节点12—节点23—节点4—配送中心。求解结果总时长为207.38min，目标函数值为2 853.469 元。

图3 车辆运输系统仿真模型

4 结 论

本文通过对城市配送中心选址规划项目调研与管理部门的协作获取论证数据展开案例分析，以国内某大型物流企业核心地区城市配送中心规划的实践研究为例，结合运输距离、建设规模和建设成本等定量因素以及选址与路由规划的相互影响、选址的多层次特性、上下级存运数量均衡等定性因素，得出如下结论：

（1） 改进多重心算法相对于传统的选址算法，不仅考虑了实际路网距离、运输成本等因素，还考虑与选址相关的定性因素，结合实际调研获取的数据进行实验对比，具有更好的求解结果，而且使选址模型更具有实际意义。

（2） 在确定了物流企业城市配送中心选址坐标后，根据案例调查获取的配送量和集货量、城市配送中心建设费用、车辆派遣费用和配送成本等数据，研究城市配送中心设立前后物流系统总费用的对比趋势，进一步验证了模型和算法的有效性，为物流企业城市配送中心选址策略制定提供有效借鉴。

基于城市配送中心选址的实践研究构建模型，将影响选址的多个因素看作一个复杂系统进行研究，在求解过程中采用改进多重心算法以及多智能体仿真建模软件，进而较好地解决了实际应用中多节点选址和车辆调度问题，求解结果也验证了模型与算法在“国内某物流大型企业城市配送中心选址规划”中的有效性和可行性。