基于变结构控制器的敏捷卫星姿态机动方法
梁 健,眭晓虹,赵 阳,蔡娅雯,张和芬
(1.北京空间飞行器总体设计部, 北京 100094;2.钱学森空间技术实验室, 北京 100094)
0 引言
随着天基遥感卫星观测能力的逐步提升,具有快速机动能力的敏捷卫星日益受到人们的关注。对地观测卫星为实现高分辨大幅宽成像、同轨立体成像以及视频成像等功能需要具备快速姿态机动和稳定的能力,同时侦察卫星为跟踪快速机动目标,对姿态快速机动能力也提出了更高的要求。和飞轮相比,控制力矩陀螺(Control Moment Gyroscope,CMG)具有强大的力矩输出和力矩放大能力,因而适合作为敏捷卫星姿态控制执行机构。然而,由于CMG结构复杂,且力矩输出存在奇异问题,因而限制了CMG的广泛应用。当前,应用CMG的敏捷卫星有Pleiades、WorldView、SPOT等系列[1]。Pleiades卫星上配备了4个安装成金字塔构型的单框架控制力矩陀螺(Single Gimbal Control Moment Gyroscope,SGCMG),每个SGCMG的角动量为15Nms,最大框架转速为3rad/s,输出力矩峰值为45Nm,平均最大输出力矩为20Nm。该SGCMG配置能使Pleiades卫星最大姿态机动角速度达到4(°)/s,并在25s内绕滚动或俯仰通道完成60°姿态机动[2]。我国也积极发展敏捷卫星平台,其中的商业遥感卫星“高景一号”的姿态机动能力与Pleiades卫星相当,具有多条带拼接、立体观测等观测模式,分辨率可达0.5m。
在诸多控制算法中,变结构控制的特点是在滑动模态下对系统参数变化和干扰具有很强的鲁棒性。正是由于这种对参数变化和外部扰动的不敏感特性,使得变结构控制算法在敏捷卫星姿态控制方面具有巨大的应用潜力[3]。
为实现敏捷卫星快速姿态机动,本文采用6个SGCMG组成的五棱锥构型作为姿态控制执行机构。为缩短卫星姿态机动所需时间,对卫星绕Euler轴进行姿态机动的角轨迹进行了规划,并根据星体实际姿态与规划姿态之间的误差四元数和误差角速度设计了变结构控制律。仿真及在轨验证结果表明,该控制律能有效完成绕Euler轴的姿态机动并具有较强的鲁棒性。
1 卫星姿态运动数学模型
带有SGCMG的刚体卫星姿态运动的动力学方程为
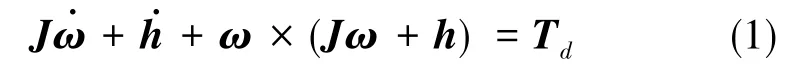
式(1)中,J为包含SGCMG系统的卫星惯量矩阵,ω为星体在惯性系下的转动角速度,h为SGCMG系统的角动量,Td为作用于星体上的外部干扰力矩。若将SGCMG系统输出的控制力矩表示为,此时,卫星姿态运动的动力学方程可以表示为

采用误差四元数表示星体的姿态运动学模型。首先,定义卫星本体相对于轨道坐标系的姿态四元数:q=[q0q1q2q3]T。其中,q0=cos(φ/2),[q1q2q3]T=nsin(φ/2),n为Euler轴方向的单位矢量,φ为绕Euler轴转过的角度,且姿态四元数满足约束条件qTq=1。在用四元数表示卫星姿态时,q和-q对应同一姿态,为消除四元数表示姿态的双重性,本文取q0>0。
设规划姿态四元数为qs,q与qs之间的误差四元数qe可表示为

采用误差四元数表示的姿态运动学方程为
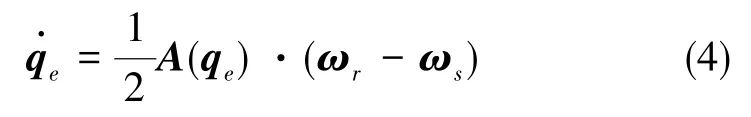
式(4)中,ωr为本体坐标系相对于轨道坐标系的姿态角速度,ωs为规划姿态角速度,A(qe)的表达式如下

本体系相对于惯性系的姿态角速度在本体系中可表示为
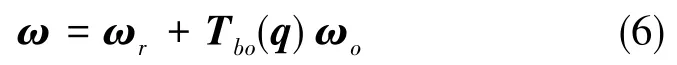
式(6)中,ωo=[0-ω00]T,ω0为轨道角速度,Tbo(q)为轨道坐标系到本体坐标系的转换矩阵,表达式为

2 SGCMG系统操纵律设计
对于单个SGCMG,其输出力矩位于与框架轴垂直的角动量面上,产生的力矩方向始终与角动量方向相互正交。如图1所示,SGCMG输出力矩方向为τi或τ′i。设期望力矩方向u在角动量面上的投影为τdi,当角动量矢量hi与期望力矩的投影τdi相互正交时,SGCMG角动量改变产生的输出力矩与期望力矩投影方向相同。此时,SGCMG在期望方向的力矩输出能力达到最大。
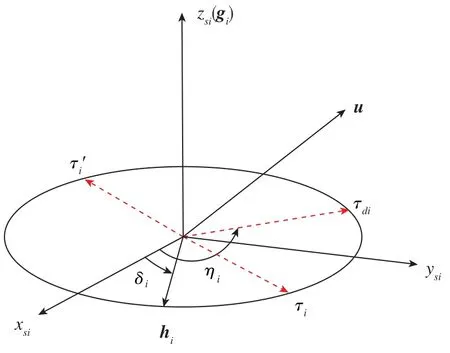
图1 SGCMG输出力矩示意图Fig.1 Schematic diagram of SGCMG output moment
对于SGCMG系统,可定义如下力矩输出性能指标

式(8)中,θi为第i个SGCMG角动量矢量hi与期望力矩的投影τdi之间的夹角,θi=δi-ηi,n为系统中SGCMG个数。S越大,表明系统在期望方向的力矩输出能力也越大;S=0表明系统各个SGCMG角动量方向均与期望力矩投影方向相同或相反,此时系统无法产生期望方向的输出力矩,系统陷入奇异状态。相对于奇异度量D,力矩输出性能指标S更能反映系统在期望方向的力矩输出性能。
框架转速指令可分解为两部分

式(9)中,为有力矩输出的转速指令,为空转指令,它们满足以下方程

零运动方程的解为
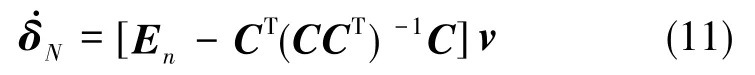
式(11)中,v为待定的n维矢量,En为n×n维的单位矩阵。
框架在转动过程中会引起力矩输出性能指标S的变化,S随框架转角变化的表达式可表示为
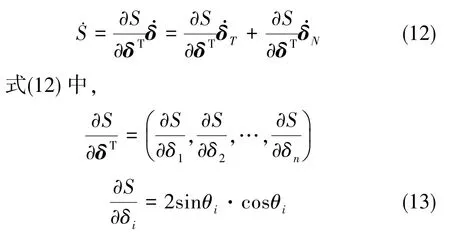
零运动控制影响表达式的第二项,令其为R

代入的表达式,可得
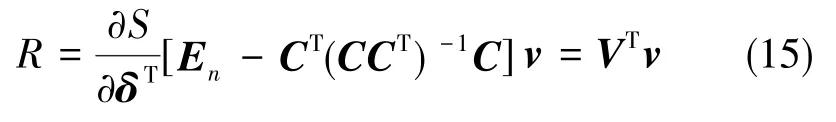

因此,基于力矩输出性能指标的零运动操纵律表达式为

零运动系数λ的大小反映了操纵律通过零运动在期望方向保持力矩输出能力的强弱程度。λ取值越大,操纵律在期望方向具有更强的力矩输出能力,由于SGCMG最大框架转速的限制,操纵律输出指令力矩能力越小;λ取值过小时,会使得系统不能在期望方向取得较大的力矩输出能力,故系数λ需合适选取。当力矩输出性能指标S较大时,系统在期望方向输出力矩能力较大,零运动系数λ可取较小值;当S较小时,系统在期望方向输出力矩能力较小,零运动系数λ应取较大值。因而,参数λ取值可写为如下形式

式(18)中,λ0>0,b>0。
3 姿态机动角轨迹规划
3.1 旋转Euler轴的确定
设星体在轨道坐标系中的初始姿态四元数为qc,目标姿态四元数为qm,初始姿态四元数与目标姿态四元数之间的误差四元数qerr可表示为
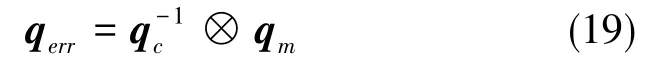
式(19)中,qerr=[qerr0qerr1qerr2qerr3]T,Euler旋转轴的指向nc在本体坐标系中表示为

绕Euler轴旋转的角度为

3.2 绕Euler轴机动的角轨迹规划
卫星进行姿态机动时,卫星最大机动角速度受到姿态控制执行机构最大输出角动量和姿态敏感器测量范围的限制。卫星进行大角度姿态机动时,绕Euler轴进行旋转机动可获得最短的姿态机动角路径[4]。设星体进行姿态机动时,所能达到的最大机动角速度为。为了节省姿态机动所需时间,将卫星绕Euler轴的姿态机动过程规划为匀加速、匀速、匀减速三个阶段。其中,匀加速、匀减速阶段能达到的最大角加速度由执行机构所能提供的最大输出力矩和星体转动惯量决定。

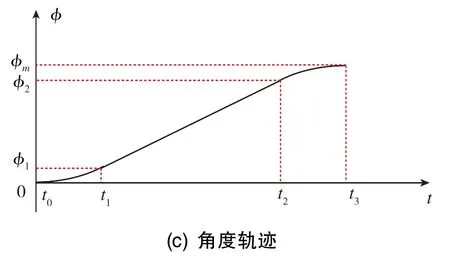
图2 角加速度、角速度、角度轨迹示意图Fig.2 Schematic diagram of angular acceleration,angular velocity and angular trajectory
图2中,t0为姿态机动开始时刻,t1为加速阶段结束时刻,t2为匀速机动结束时刻,t3为减少阶段结束时刻。

姿态机动过程中,角加速度可表示为

机动角速度为
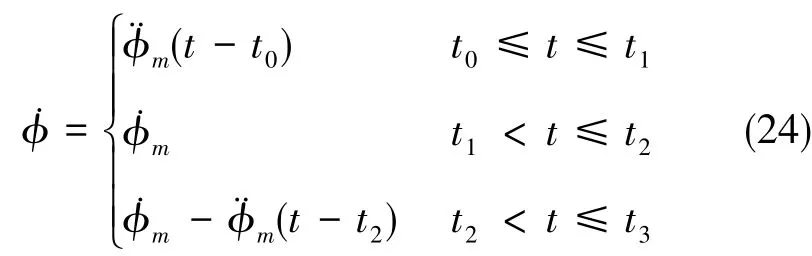
机动角度为
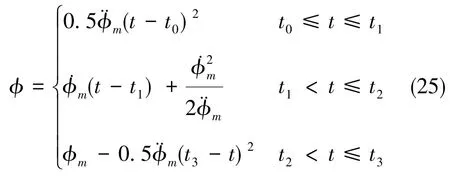
星体自初始姿态qc绕Euler轴nc旋转角度φ后的规划姿态四元数qs可表示为

q与qs之间的误差四元数表示为qe,则。绕Euler轴的旋转角速度在本体三轴上的分量可表示为

4 变结构控制器设计
为实现卫星绕Euler轴按规划的角度、角速度轨迹完成姿态机动,设计了以下变结构控制器。
4.1 滑动模态设计
设计滑动模态如下

式(28)中,G为正定对角矩阵,qe13=[qe1qe2qe3]T。系统在滑动模态上运动时,s=0,取Lyapunov函数
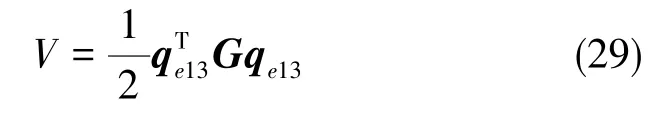
V≥0,当且仅当qe13=0,即q=qs时,V=0。因此,V为正定函数。对Lyapunov函数求导,可得
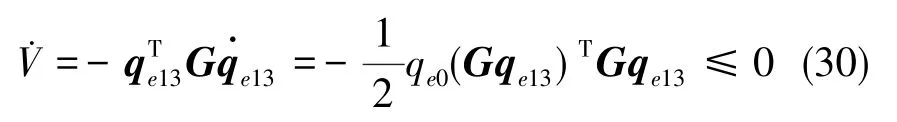
当且仅当qe13=0时,0。因此,系统在滑动模态上是渐进稳定的。
4.2 变结构控制律设计
对s求导,可得
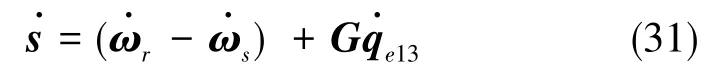
为保证滑动模态的可达性,选择以下形式的趋近律

式(32)中,K、W均为正定对角矩阵,进而可得
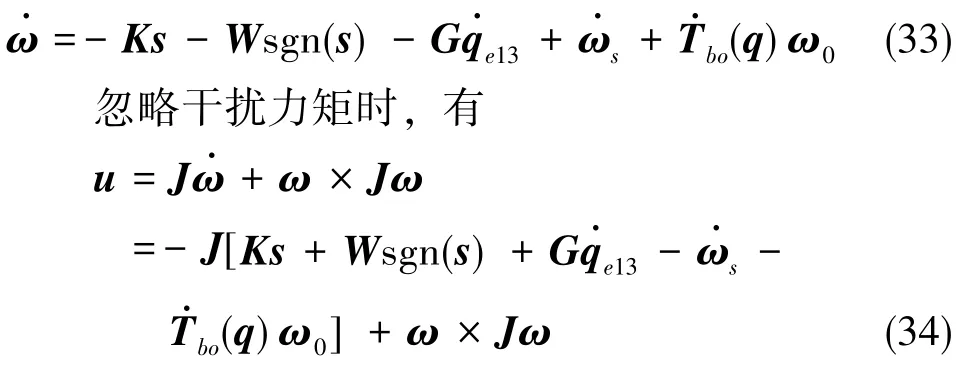
4.3 鲁棒性分析
设卫星转动惯量标称值为J0,当系统中存在模型误差ΔJ和外部干扰力矩Td时,经推导可得出

式(36)中,wi(i=1,2,3)为W矩阵对角线上的三个元素。wi的取值越大,系统抗干扰能力越强,但不连续控制引起的抖动也会更剧烈。为减小抖动对系统的影响,用饱和函数sat(s)代替sgn(s),sat(s)函数定义如下

式(37)中,si为滑模面s的第i个分量,ε为一适当的小正数。
以上通过将符号函数sgn(s)用饱和函数sat(s)代替,在一定程度上减弱了因符号函数引起的系统抖振,但饱和函数项仍会使得系统存在一定的抖动,从而影响到卫星姿态稳定控制的精度。为提高变结构控制方法的姿态稳定控制精度,以及降低执行机构的工作负担,将饱和函数sat(s)做如下改进。
改进的饱和函数sat′(s)定义为[5]
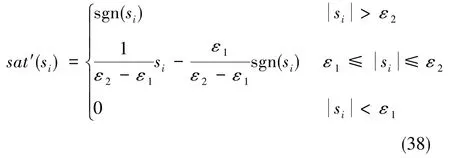
式(38)中,ε1、ε2为改进的饱和函数sat′(s)的两个边界值,且有0<ε1<ε2。sat′(s)的示意图如图3所示。
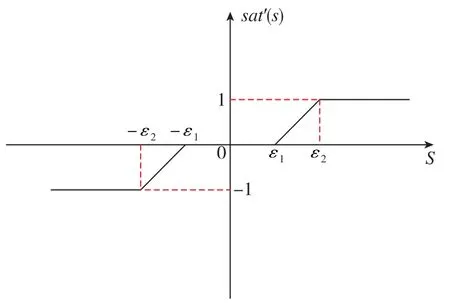
图3 饱和函数示意图Fig.3 Schematic diagram of saturation function
对于以上改进后的饱和函数sat′(s),当ε1时,sat′(s)表现出与sat(s)相同的性质;不同之处在于,当时,sat′(s)=0,控制器中的饱和函数项sat′(s)不再发挥作用,从而不会引起系统的抖动。此时,变结构控制参数中仅K、C产生控制作用,变结构控制器已退化为PD控制器。为了达到进一步削弱系统抖动的目的,当卫星长期维持在要求稳定姿态精度时,应使得。本文取
5 仿真结果及分析

基于设定的仿真参数,分别对标称惯量、惯量矩阵增加50%以及惯量矩阵减小50%的情况进行仿真分析,仿真结果如图4~图9所示,不同惯量下三轴稳定时间如表1所示。
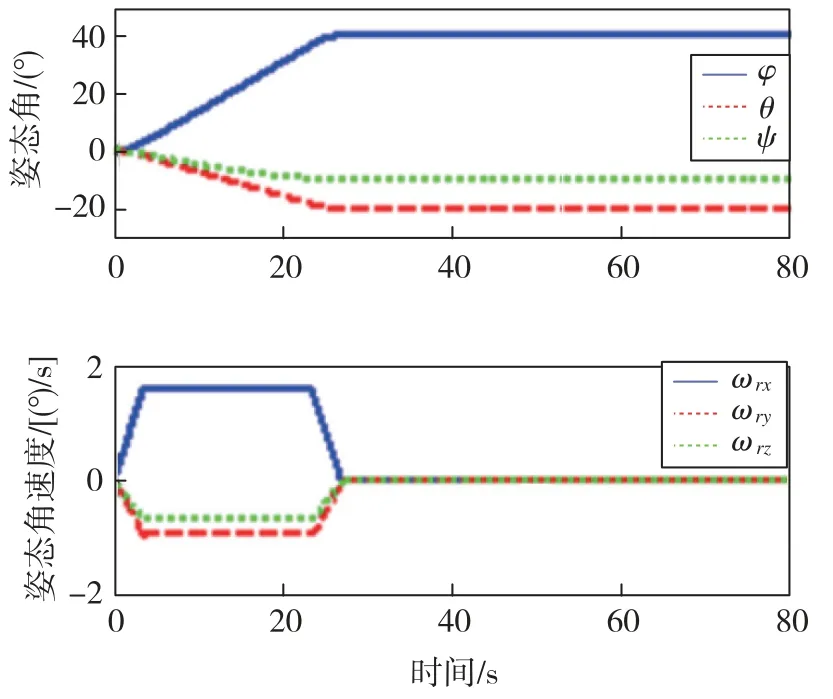
图4 星体姿态角、姿态角速度变化曲线(J0)Fig.4 Curves of attitude angle and attitude angular velocity(J0)

图5 三轴输出力矩、角动量、奇异度量值变化曲线(J0)Fig.5 Curves of triaxial output moment,angular momentum and singularity degree(J0)

图6 星体姿态角、姿态角速度变化曲线(1.5J0)Fig.6 Curves of attitude angle and attitude angular velocity(1.5 J 0)
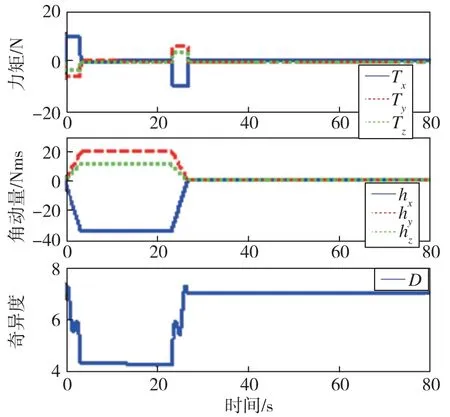
图7 三轴输出力矩、角动量、奇异度量值变化曲线(1.5J0)Fig.7 Curves of triaxial output moment,angular momentum and singularity degree(1.5J0)
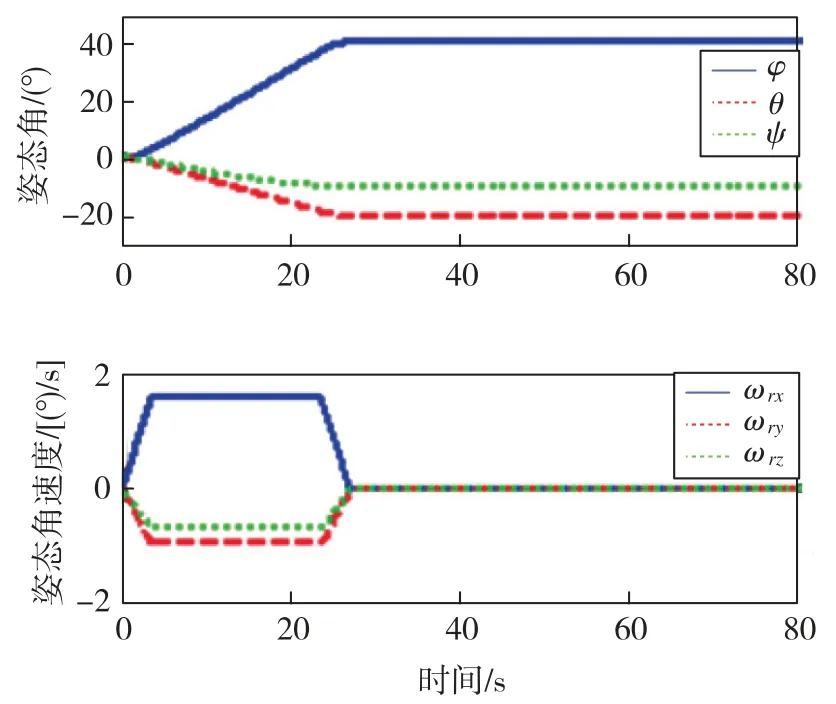
图8 星体姿态角、姿态角速度变化曲线(0.5J0)Fig.8 Curves of attitude angle and attitude angular velocity(0.5 J 0)
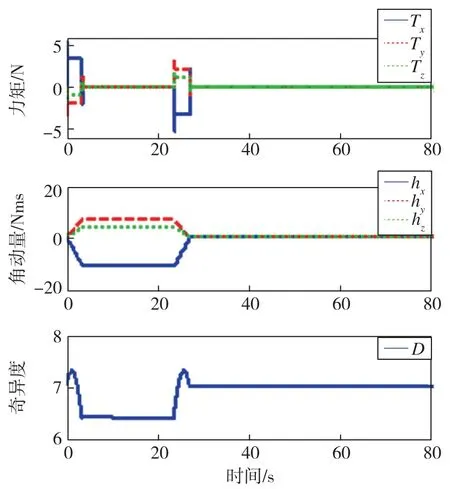
图9 三轴输出力矩、角动量、奇异度量值变化曲线(0.5J0)Fig.9 Curves of triaxial output moment,angular momentum and singularity degree(0.5J0)

表1 三轴姿态稳定所需时间对比Table 1 Comparison of the time required for triaxial attitude stabilization
分析以上仿真结果可知:1)本文设计的变结构控制器能够按要求完成绕Euler轴进行的大角度姿态机动,并达到指标要求的指向精度和稳定度;2)将卫星转动惯量增大或减小50%时,卫星姿态角、姿态角速度变化曲线无明显差异,三轴稳定时间基本一致,验证了控制系统具有较强的鲁棒性;3)姿态机动过程中,SGCMG系统始终远离奇异状态。
6 在轨验证
本文提出的姿态机动方法已成功应用于我国某商业遥感小卫星,该卫星于2018年成功发射入轨,控制分系统在轨表现稳定,机动能力满足设计要求。图10、图11分别为进行某一次变轨期间停止偏航角修正以及完成变轨后重新引入偏航角修正的过程中卫星的三轴姿态角及角速度曲线,可以看出,其姿态机动时间及稳定时间都满足设计要求,设计的控制率满足应用要求。目前,卫星在轨表现优异,为我国商业遥感卫星的发展奠定了良好的基础。
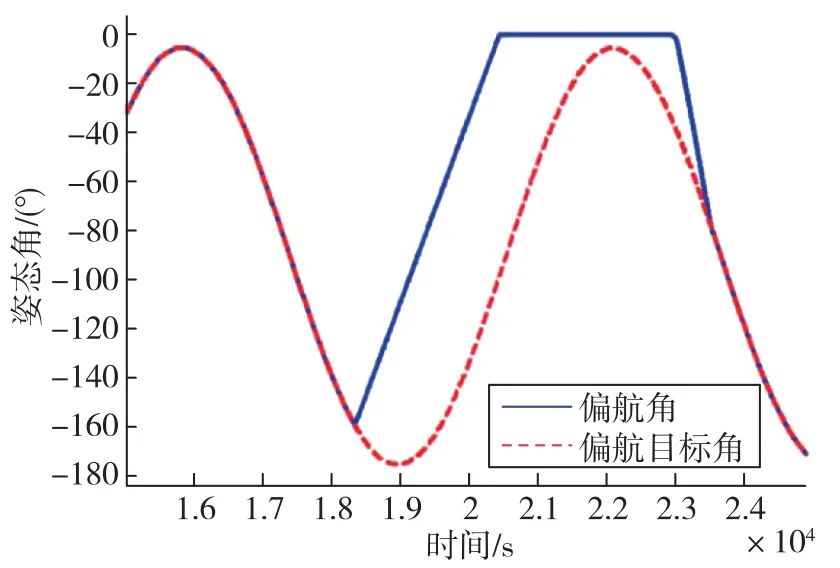
图10 偏航角及偏航目标角曲线Fig.10 Curves of yaw angle and target drift angle
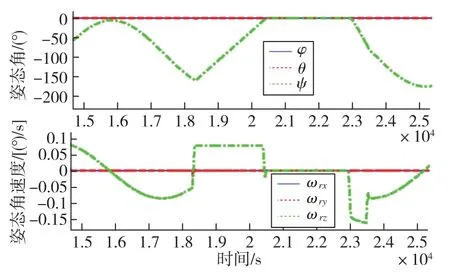
图11 变轨后的姿态角及角速度曲线Fig.11 Curves of attitude angle and attitude angular velocity after orbit maneuver
7 结论
为实现敏捷卫星快速姿态机动,本文对绕Euler轴进行姿态机动的角轨迹进行了规划,将姿态机动过程划分为匀加速、匀速和匀减速三个阶段。为完成对规划姿态的跟踪,本文设计了基于误差四元数和误差角速度的变结构控制律,并以由6个SGCMG组成的五棱锥构型作为姿态控制系统执行机构。仿真及在轨验证结果表明,该控制算法能有效完成姿态机动控制任务,且对卫星参数变化不敏感,体现出较强的鲁棒性和良好的控制性能,本文的研究成果对敏捷卫星姿态控制器的设计具有一定的指导意义。

