基于M-K模型的TA15钛合金高温成形极限

毕静，马博林，张艳苓，4，张志，4，吴向东，*

（1.中国航空制造技术研究院，北京100024； 2.塑性成形技术航空技术重点实验室，北京100024；3.北京航空航天大学 机械工程及自动化学院，北京100083； 4.数字化塑性成形技术及装备北京市重点实验室，北京100024）

TA15钛合金属于一种近α型钛合金，由于其在高温条件下具有较好的强度和热稳定性，在高性能飞机重要构件的制造中得到了广泛的应用［1-2］。在高温成形工艺中，温度和应变速率对TA15钛合金的微观组织有着明显影响［3-4］，进一步影响其宏观高温变形行为［5-7］。对于TA15钛合金板料，其高温环境下的成形极限曲线（Forming Limit Curve，FLC）对于衡量TA15高温变形能力及优化高温成形工艺参数有至关重要的作用，因此，研究温度等工艺参数对TA15钛合金高温成形极限曲线的影响有重要实际意义。

金属板料的成形极限曲线由不同应力或应变状态下的应变对构成，一般情况下通过拉伸处于不同应力或应变状态下的金属板料可获得其极限应变，主要试验方法包括Nakajima试验法及M-K试验法等。此外，结合失稳理论也可对金属板料成形极限曲线进行理论预测。目前应用最为广泛的失稳理论是Marciniak和Kazim ierz提出的凹槽理论，简称为M-K失稳理论［8］。考虑到屈服准则及强化规律，利用该理论可实现金属板料在不同温度及应变速率下的成形极限曲线理论预测。然而该理论预测结果严重依赖于初始厚度不均匀度，往往需要通过与试验数据对比才可获得较为精确的预测结果。

考虑到高温环境下的试验复杂性，对于金属板料，特别是钛合金板料，其高温环境下的成形极限研究相对较少。马博林等［9］利用电磁感应加热原理，搭建了高温环境下的成形极限试验平台，并获得了TC4钛合金在650～750℃下的成形极限曲线。王承鑫［10］设计了高温成形极限试验模具，从试验角度研究了温度参数对TC4及Bti-6431S等钛合金成形极限的影响规律。申发兰［11］从试验角度出发，分析了温度及应变速率等参数对TA15钛合金高温力学性能、成形极限及拉伸性能的影响规律。Ma等［12］分析了TA15钛合金高温胀形过程中的板料温度变化状态，研究了温度分布及变化对高温胀形性能的影响规律，并获得了其高温成形极限数据。Yang等［13-14］通过高温单拉试验，分析了流动软化现象对TA15钛合金高温力学性能及任性破裂行为的影响，从理论角度分析了不同模型参数其理论成形极限的影响规律。通过上述文献可以看出，目前研究以钛合金高温力学性能研究为主，而针对其高温成形极限研究则以试验研究为主，理论研究方面还需要一定的工作。

本文考虑材料在高温环境下的软化效应，建立TA15钛合金高温本构模型，利用M-K失稳理论对TA15钛合金高温成形极限进行了理论预测。分析了加工硬化指数n、速率敏感因子m及软化因子n1等因素对理论成形极限曲线的影响，为进一步开展高温环境下板料成形极限的研究奠定了基础。

1 TA15钛合金高温性能试验

1.1 高温单向拉伸试验

本次试验选用的TA15钛合金板料厚度为1mm，其微观组织及化学成分分别如图1及表1所示。试验温度为800、840、880℃，应变速率为0.01／s。高温单向拉伸试验用的试样及拉伸后试样如图2所示。

图1 TA15钛合金板微观组织Fig.1 Microstructure of TA15 titanium alloy plate

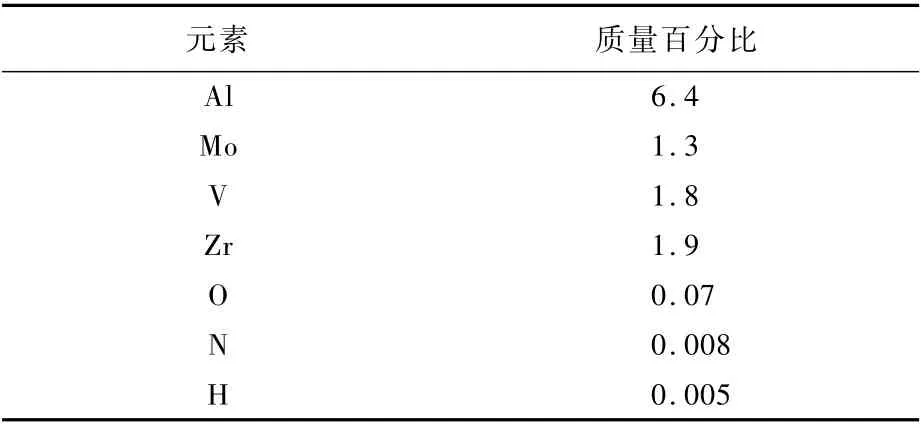
表1 TA15钛合金板化学成分Table 1 Chem ical com positions of TA15 titanium alloy p late

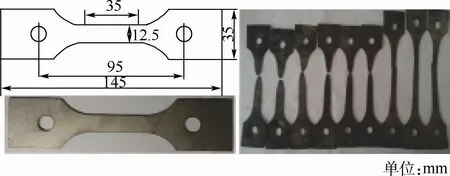
图2 高温拉伸试样及尺寸Fig.2 Hot tensile specimens with its size

考虑到高温软化因素及加工硬化因素，本文选用的高温本构方程为

式中：σi为应力；K为强度因子；T为温度；εi为应变；˙εi为应变速率。

在式（1）中，速率敏感因子m表征了应变速率变化时材料变形强化的趋势。在本文中，认为该参数只与温度T有关，根据文献［15］，速率敏感因子m（T）的表达式为0.431-0.345（1 000／T）。在此基础之上，对试验数据进行拟合，获取不同温度下的加工硬化指数n、软化因子n1及强度因子K值。根据获得的参数值随温度的变化规律，建立加工硬化指数n（T）、软化因子n1（T）及强度因子K（T）的表达式为

拟合曲线与试验数据对比如图3所示，可以看出，利用式（1）及式（2）可以较好地描述TA15钛合金高温条件下的变形行为。此外，从式（2）及图3可以看出，随着温度升高，TA15钛合金板料的强度下降，变形抗力降低，加工硬化现象得到削弱，高温软化作用加强，板料的成形能力得到进一步提升。

1.2 高温成形极限试验

为了获得不同应变路径下的应变极限，本次高温成形极限试验方法为Nakajima试验法，用到的试样尺寸及试验设备分别如图4及图5所示。如图5所示，该高温试验系统利用感应线圈将石墨板及模具加热至所需温度，随后利用石墨板对板料进行加热。在试验过程中，高温凸模与板料发生接触，两者之间发生接触换热，由高温凸模可保证试验过程中的板料温度。

图3 热单拉试验数据与拟合曲线对比Fig.3 Comparison between hot tensile test data and fitted curves

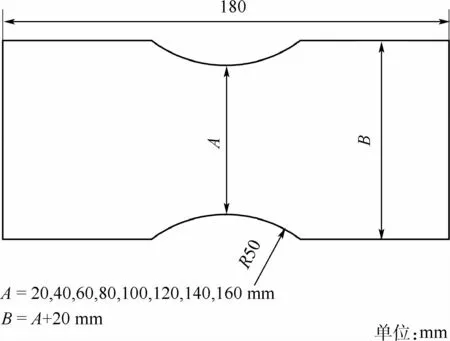
图4 高温成形极限试样尺寸Fig.4 Size of hot forming limit specimens

图5 高温成形极限试验系统Fig.5 Hot forming limit test system

在高温胀形试验前，将凸模及石墨板升温至880℃，压边圈及凹模升温至600℃，温差为±10℃。同时，在TA15钛合金板试样上印制直径2.5mm网格并进行防氧化处理，随后放置于石墨板上进行加热。在高温成形极限试验过程中，刚性凸模速度为80 mm／m in，压边力保持恒定，其大小为50 kN。当试样发生破裂时试验停止，随后对试样上网格的长度及宽度进行测量，进一步换算成应变投影于应变空间，即可获得高温成形极限数据。

根据上述试验流程，获得的TA15钛合金板料在880℃下的高温成形极限试样及数据如图6所示。可以看出，高温变形情况下TA15钛合金变形能力得到了大幅度提升，其平面应变状态下的主应变极限可达0.4左右。

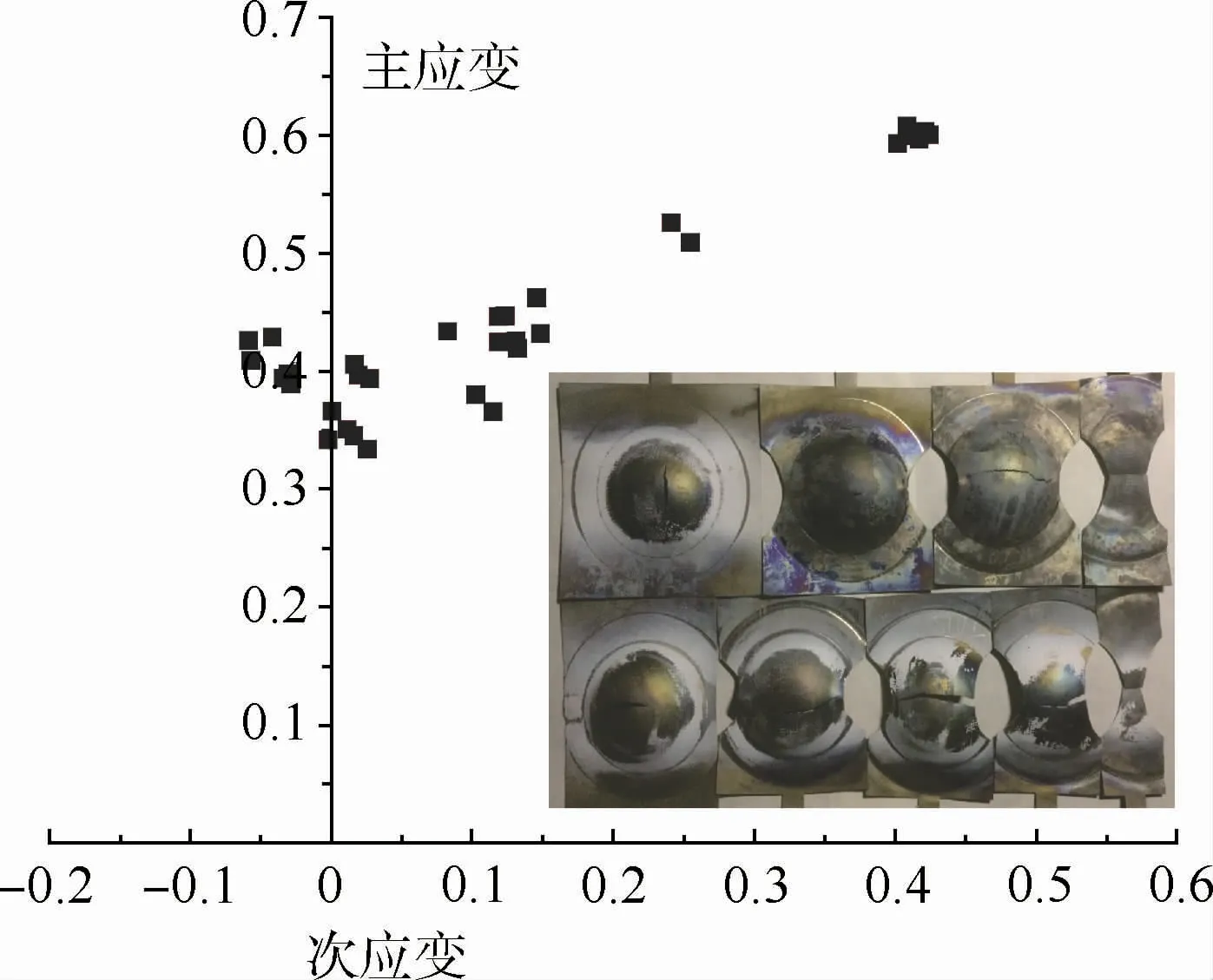
图6 TA15钛合金高温成形极限试验结果（880℃）Fig.6 Hot forming limit test results of TA15 titanium alloy（880℃）

2 TA15高温成形极限理论预测

M-K失稳理论作为一种塑性失稳理论，结合相应的屈服强化规律可对金属板料的成形极限进行理论预测，该模型示意图如图7所示。假设板料厚度方向存在一定的不均性，即存在一方向与主应力方向夹角为φ的沟槽，沟槽法线方向及切线方向分别为s与t，厚度方向的不均匀度可写为f0＝tb／ta，其中ta及tb分别表示沟槽外及沟槽内的厚度。

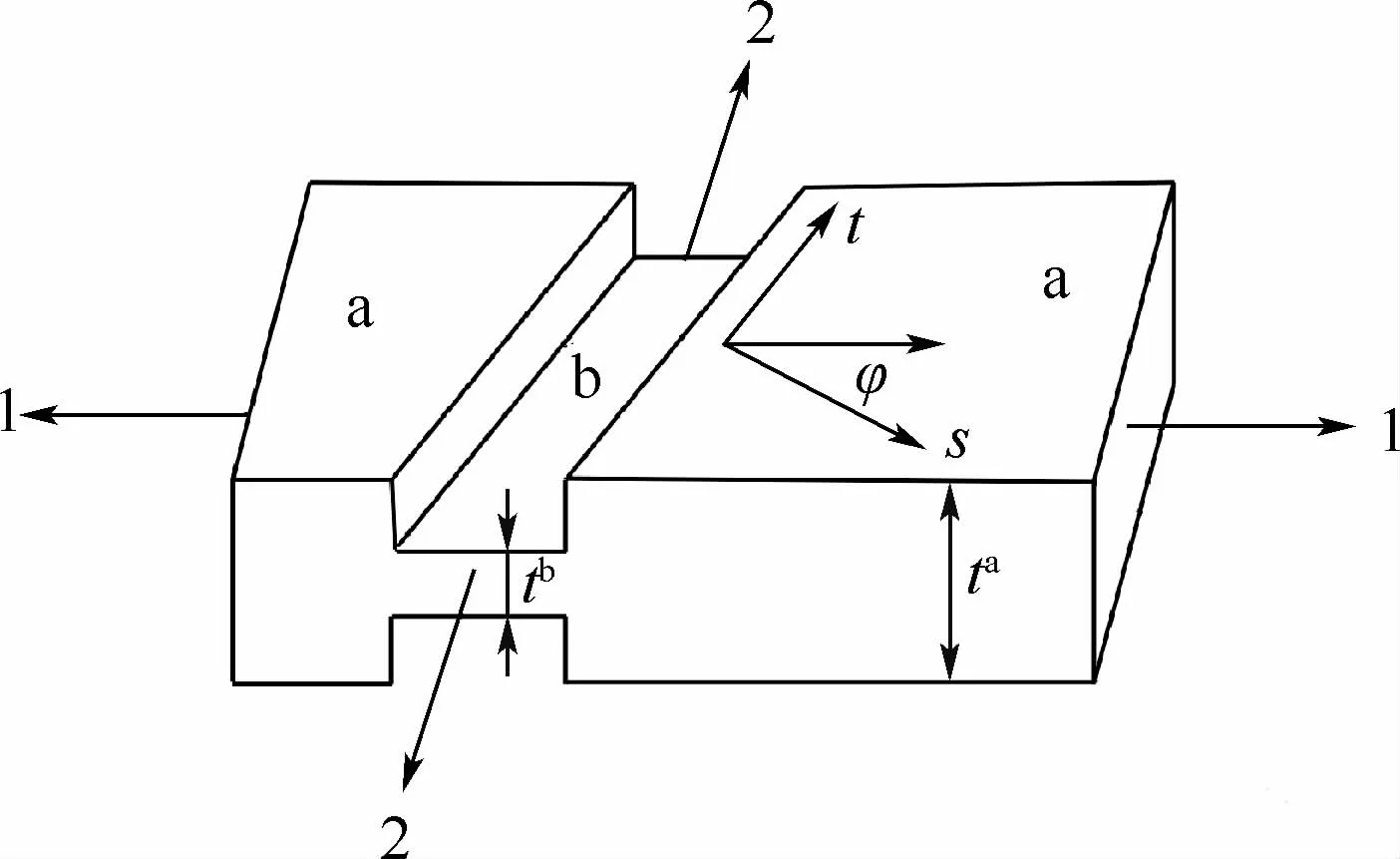
图7 M-K失稳理论模型Fig.7 M-K instability theory model

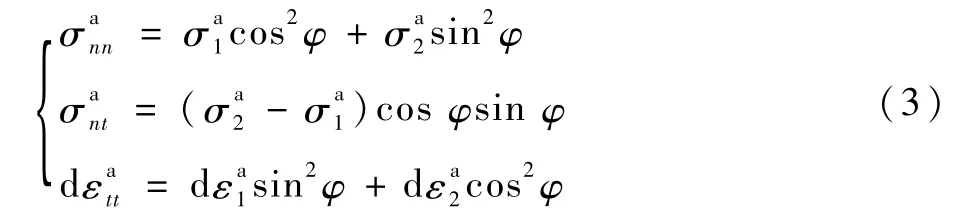
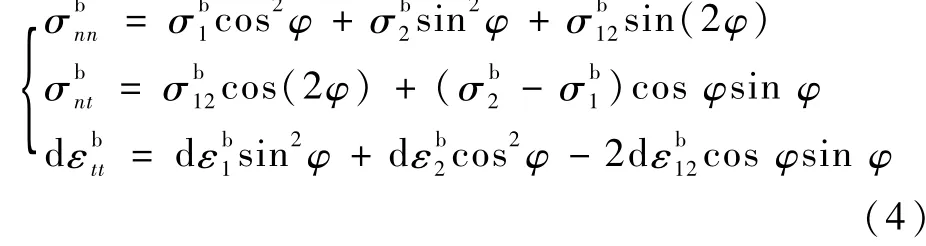
在M-K失稳理论的加载过程中，除了沟槽不均匀度之外，还需要满足力平衡条件及变形协调条件，两种边界条件分别可表示为

同时，沟槽角度φ在计算过程中需按照式（7）更新：

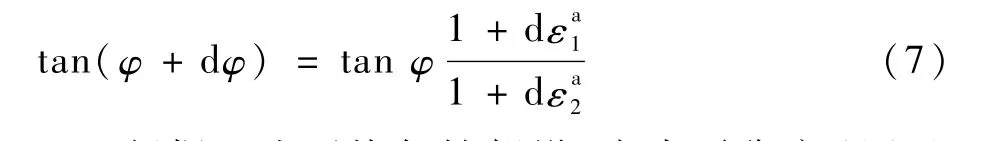
根据上述不均匀性假设，由力平衡方程（5）及变形协调方程（6）为条件，结合相应的屈服函数及材料本构模型，即可实现不同应变状态下的极限应变的预测，具体步骤可描述如下：

步骤1 在特定沟槽外应力状态比αa＝（0＜αa＜1）下给定主应变增量为，通过相应的屈服准则及材料流动法则，即可获得沟槽外a区次应变增量及等效应变增量。

步骤3 根据式（5）及式（6），利用牛顿迭代法对沟槽外参数进行求解，求解误差小于1×10-10。

步骤5 在不同沟槽角度下计算极限应变对，选取极限主应变最小的应变对作为成形极限的理论预测结果。

步骤6 更新沟槽外应力状态比αa，继续重复步骤1～步骤5。

在TA15钛合金高温成形极限理论预测过程中，沟槽外主应变增量大小为0.0005，选用Hill48屈服准则，在忽略面内各向异性的情况下，其表达式为

式中：参数F、H、G及N与各向异性指数r有关，其大小分别可表示为F＝G＝1／（1＋r），H＝r／（1＋r），N＝（1＋2 r）／（1＋r）。根据文献［12］，r取值为1.15。

在不同初始沟槽不均匀f0下，通过将理论计算的平面应变状态下的极限主应变与试验数据对比，可获得合理的f0值。针对该TA15钛合金板料，通过不同f0值下平面应变状态下的理论极限主应变大小与试验数据的对比，最终选取f0值为0.999 95。预测的整条曲线与试验结果对比如图8所示，可以看出，M-K失稳理论通过调整相应的初始沟槽不均匀度，可以很好地预测TA15钛合金板料在高温环境下的成形极限曲线。

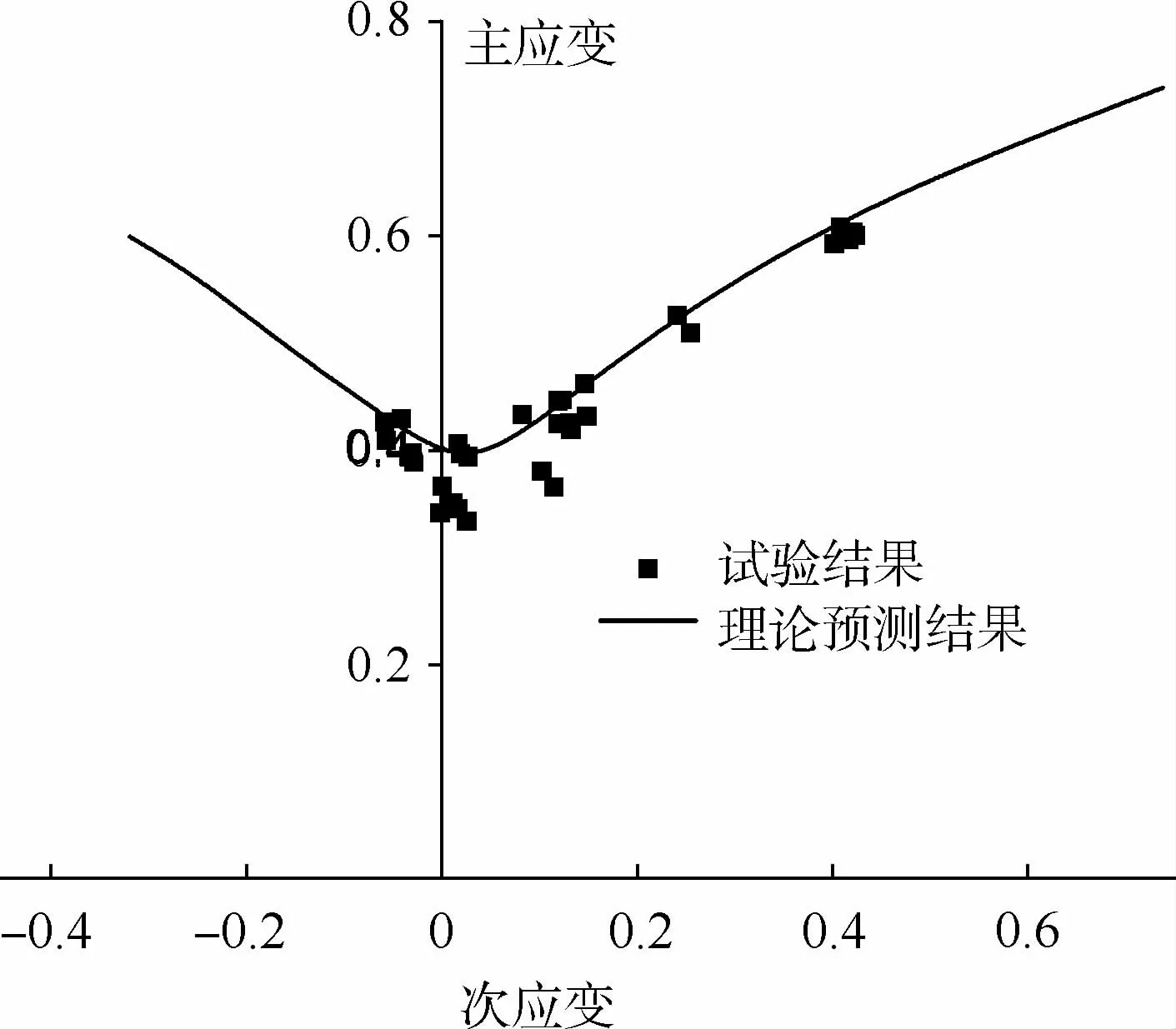
图8 理论预测结果与试验结果对比Fig.8 Comparison between theory prediction result and test result

3 本构关系对成形极限的影响

根据式（1），TA15钛合金高温板料的流变应力与温度T、速率敏感因子m、加工硬化指数n及软化系数n1均有关系。因此，分析不同参数对成形极限曲线的影响是十分必要的。

在理论预测计算过程中，首先通过式（2）及速率敏感因子的表达式确定不同温度下的n、n1、K及m值，随后将获得的参数值代入式（1），在f0为0.999 95的情况下，利用M-K失稳理论对高温成形极限进行预测，获得的不同温度状态下的理论预测曲线如图9所示。可以看出，板料成形极限随着温度的升高而升高，当温度由800℃升至880℃时，平面应变状态下主应变由0.18增至0.33，表明提升成形温度有助于改善材料成形性能，获得更大变形量。

根据式（2）可以得出，880℃下TA15钛合金的硬化指数n、速率敏感因子m及软化因子n1依次为0.392、0.0475及1.332。在此基础之上，通过改变本构模型中的上述参数，研究其对TA15钛合金成形极限的影响规律。

图10给出了不同加工硬化指数n值下的MK失稳理论预测结果，可以看出，随着加工硬化指数的增加，成形极限曲线在应变空间中的位置得到了提升。同时图10表明加工硬化指数的变化对成形极限曲线左右侧的影响基本一致，即整体提升曲线位置。

图11给出了不同速率敏感因子m下的M-K失稳理论预测曲线。可以看出，预测的成形极限曲线位置随着速率敏感因子m的增加而得到提升。与加工硬化指数n不同的是，m值的变化对成形极限左右两侧影响不一。根据图11可以很清楚地看出，速率敏感因子m的增大，对于成形极限曲线左侧的提升幅度远远大于其对曲线右侧的提升程度，即曲线逐渐变平。

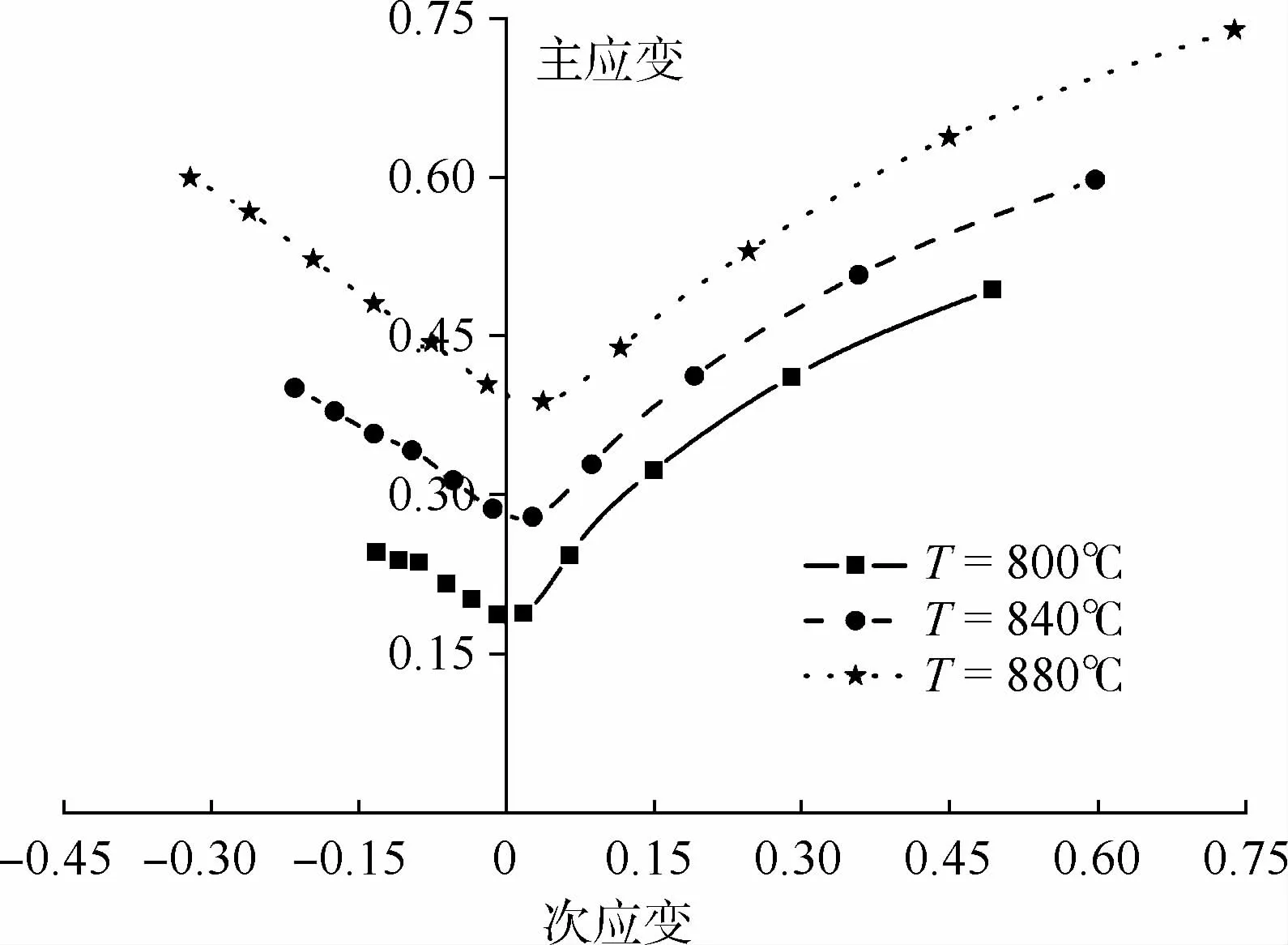
图9 温度对成形极限曲线的影响Fig.9 Effect of temperature on FLC

图10 加工硬化指数n值对成形极限曲线的影响Fig.10 Effect of hardening index n on FLC

不同软化因子n1值（负值）下的理论预测成形极限如图12所示。可以看出，随着n1值的增加，预测曲线位置得到提升。由式（1）及图3可以看出，随着应变的增加，加工硬化指数使得应力提升，而软化因子降低应力，可以认为软化因子与加工硬化指数对应力大小的影响是相互对立。对比图10及图12可以看出，随着n1值趋于0，相当于提升了加工硬化指数n，使得理论预测成形极限曲线的位置得到了提升。

由图9～图12分别可以看出，本构关系中的参数对成形极限有着重要影响，提升成形温度，增加加工硬化指数、速率敏感因子及软化因子，均可以使得理论预测成形极限曲线在应变空间的位置得到提升。根据M-K失稳理论，沟槽内外应力状态在不同屈服轨迹上演化，随着沟槽内的应变状态趋于平面应变状态，导致沟槽内外第一应变增量比逐渐增大，最终达到材料失效判据标准。很明显，当采取应力应变关系表达式导致应变强化率不同，当强化率越大时，导致预测的成形极限曲线的位置越高。由式（1）可以得出，应变强化率h＝dσ／dε＝Kσ（n／ε-nlε）。根据应变强化率可以看出，硬化指数n值与软化因子nl值对强化率的影响是相互对立，即提升n值或减少nl值均会使得强化率增加，使得图10及图12中的成形极限曲线位置得到提升。

图11 速率敏感因子m值对成形极限曲线的影响Fig.11 Effect of strain rate sensitivity factor m on FLC

图12 软化因子n1 值对成形极限曲线的影响Fig.12 Effect of softening factor n1 on FLC

此外，应变强化率h还依赖于应力σ，而提升速率敏感因子会使得应力降低，进一步降低应变强化率h，因此图11中提升速率敏感因子可提高成形极限位置。此外，由图3可以看出，由于软化因素使得应力随着应变的增加而逐渐降低，因此，不同变形阶段速率敏感因子对强化率的影响亦不相同。在小变形阶段，如图11中的单向应力状态及平面应变状态下，材料失效时等效应变较小，此时应力较大，提升速率敏感因子可显著降低应变强化率h，因此使得成形极限曲线得到显著提升；而当等效应变较大时（如图11中的双向拉伸应变状），应力值较小，提升速率敏感因子对应变强化率h的降低影响较小，因而使得成形极限曲线右侧的提升不如曲线左侧。

4 结 论

本文建立了考虑高温软化效果的TA15钛合金高温本构模型，利用高温成形极限试验系统获得了TA15钛合金在880℃下的成形极限曲线，并利用M-K失稳理论对不同温度及本构参数下的成形极限曲线进行了理论预测，结果表明：

1）TA15钛合金高温成形性能随温度的提升而得到改进，当温度从800℃升温至880℃时，平面应变状态下的极限主应变由0.18升至0.33，曲线位置得到大幅度提升。

2）本构关系中的参数对成形极限曲线理论预测结果的影响取决于该参数对强化率的影响，提高加工硬化指数、速率敏感因子及降低软化因子使得强化率增加，进一步提升成形极限曲线在应变空间中的位置。