基于CFD／CSD松耦合的直升机配平分析方法

余瑾，王松，刘勇，杨卫东

（南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京210016）

在直升机旋翼动力学分析中，配平计算不仅是飞行力学和操纵品质分析的基础，旋翼的配平解对旋翼的气弹稳定性和气弹载荷分析也有着至关重要的影响［1］。直升机旋翼气弹分析是一个具有挑战性的多学科问题，精确的桨叶气动建模涉及到三维非定常流场、跨声速流、动态失速、桨叶刚体运动和弹性变形等，这就必须与CSD分析相结合进行综合分析。在完全耦合的气弹分析中，由于桨叶的刚体运动、弹性变形、气动载荷和旋翼配平状态相互影响，桨叶的气动力计算和结构动力学分析也是相互依赖、相互作用的。为了解决这一复杂问题，旋翼综合分析代码往往采用基于升力线理论和查表法等简化的空气动力学模型，然而使用这些快速方法进行载荷预测，往往会显示出明显的不足，难以描述细致的流场细节，无法满足气弹载荷分析的精度要求［2］。本文的研究目的就是将CFD求解器耦合进气弹综合分析代码中，以提供高保真的气动模型，克服气弹综合分析中气动模型精度不足的缺陷，而气弹分析模块则依然进行结构动力学和配平分析。

CFD模块与气弹综合分析模块的耦合有2种思路：松耦合和紧耦合。在松耦合策略中，CFD模块和CSD模块分别在时域内推进，每隔一段时间（如旋翼旋转一圈）交互一次数据；在紧耦合策略中，CFD模块和CSD模块集成在一起，每个时间步长上都要进行数据交换。尽管紧耦合策略更为严密，但必须要在CFD／CSD两个模块间的时间精度控制和数据交换效率上付出更高的代价。另一方面，配平分析至少包含2层循环：外层配平迭代循环和内层气弹分析响应求解迭代循环。采用紧耦合策略进行配平计算意味着将CFD求解器放进了内层的响应求解迭代运算，为此将付出更大的计算代价。Johnson等［2］指出，就当前的计算能力而言，是禁止将CFD技术直接引入到配平循环内的。因此，将紧耦合方法用于配平分析是不妥的。而松耦合策略允许采用模块化方法，各学科模块根据需要处理其时间精度，配平解则是综合分析的自然结果。

Tung等［3］于1986年提出了CFD／CSD之间的松耦合方法，其中CFD求解器运用小扰动方程，CSD求解器基于CAMRAD平台，通过升力线法修正CFD计算的气动力，在该模型中，通过CSD模块更新入流角从而修正物面无穿透条件代替驱动网格变形，该方法中CFD计算精度不足，故耦合存在收敛的问题。CFD／CSD松耦合的概念提出之后，被广泛认可和应用。2001年，Costes等［4］基于松耦合方法，运用WAVES的CFD求解器和HOST的CSD求解器，进行弹性旋翼桨叶前飞状态的配平计算，研究表明该方法对变距力矩和扭转载荷的预估具有较大的提高。2006年，Johnson等［2］基于CFD／CSD松耦合的方法，CSD求解器使用CAMRAD平台，CFD模块则基于OVERFLOW 求解器，以UH-60A黑鹰直升机为算例，对旋翼不同飞行状态下进行振动载荷的预估，取得较好的成果，并成功捕捉到桨尖涡现象，该方法具有很好的稳定性、收敛性及鲁棒性，并且对法向力和变距力矩的幅值和相位的预测与飞行测试数据具有很好的吻合，且没有使用修正物面无穿透条件代替驱动网格变形，而是通过OVERFLOW的动网格和“网格挖洞”技术实现。2006年，Chopra等［5］建立基于UMARC的CSD综合分析平台和基于雷诺平均的Navier-Stokes方程的CFD模型，采用松耦合的方法对UH-60A直升机旋翼高速前飞状态的振动载荷进行了预估，分析表明二阶精确非线性梁理论对高速前飞状态的结构动载荷具有较好的预估能力，并且准确预估到1～3阶扭转谐波载荷。国内基于CFD／CSD耦合的方法对飞行器研究相对较晚。2010年，王海［6］采用以嵌套网格为基础的CFD模块，提出直升机旋翼CFD／CSD松耦合分析方法。2013年，王俊毅、招启军［7］发展了旋翼稳态前飞状态的CFD／CSD耦合分析方法，研究表明，改变剖面的扭转刚度旋翼气动载荷变化较大。2014年，肖宇、徐国华等［8］基于非惯性系下的Navier-Stokes方程，改进了悬停状态下的CFD／CSD耦合研究方法，UH-60A直升机的算例表明耦合策略具有更好的载荷预估能力。2015年，李建东［9］发展了二维翼型的CFD／CSD紧耦合策略。2016年，黄道博［10］基于CFD／CSD耦合方法准确预估了直升机稳态前飞状态旋翼气动载荷和振动载荷。CFD模块以FLUENT商用软件为平台，CSD模块基于中等变形梁理论，通过UDF进行桨叶运动和网格变形信息的交换。

在本文采用的CFD／CSD松耦合策略中，CFD模块和CSD模块分别在时域内推进，以桨叶弹性轴和变距轴线为媒介，通过线性插值方法交换气动载荷和响应数据，旋翼每旋转一圈交互一次。在耦合迭代过程中，随着气动载荷的改变，改变旋翼的操纵量和飞行姿态以满足配平方程组。本文构造了内外两层迭代：内层迭代为配平求解过程，随着气动载荷的改变，以牛顿迭代法改变旋翼的操纵量和飞行姿态，满足配平方程组；外层循环即以CFD模块计算的气动力来修正配平计算中气弹分析的气动力输入，直到配平量和CFD气动力在外层迭代中不再变化，达到同时收敛，即得到了耦合配平解。

1 旋翼流场CFD建模

直升机旋翼CFD技术一直以来是计算流体力学领域的热点和较为困难的问题之一，这与直升机旋翼的复杂工作环境及旋翼特有的运动和操纵方式有关。网格是CFD计算的基础，就直升机旋翼而言，计算空间生成单一的计算网格是相当困难的，这会使得网格局部存在严重的扭曲或畸变，故目前多采用多个分区对接及重叠嵌套网格避免这一问题。本文基于OversetGrid网格前处理软件绘制直升机旋翼嵌套网格，基于OverCFD软件，综合考虑旋翼桨叶运动与变形、网格自适应、“网格挖洞”与插值、湍流模型等计算旋翼流场信息。

1.1 适合CFD使用的控制方程

流体运动的基本规律需满足物理学三大定律，即质量守恒定律、动量守恒定律及能量守恒定律。

一般局部坐标系下的Navier-Stokes方程具有如下形式［11］：

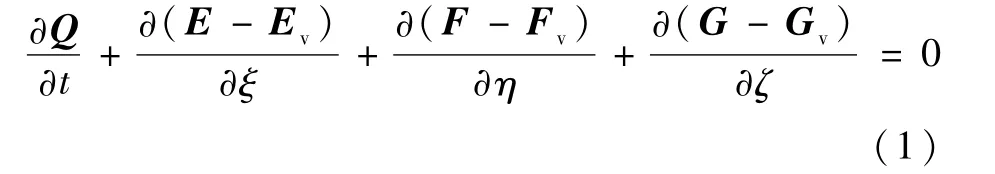
式中：ξ、η、ζ分别为微元体的一般局部坐标系3个方向；守恒变量为其中：ρ为流体密度；u、v、w分别为笛卡儿坐标xy-z三个方向上的绝对速度分量；e0和ei分别为总能量和内能。

无黏通量为

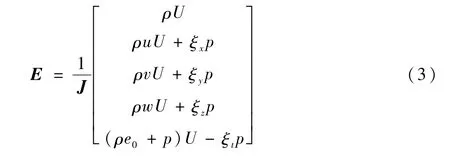
式中：p为压强。

黏性项为

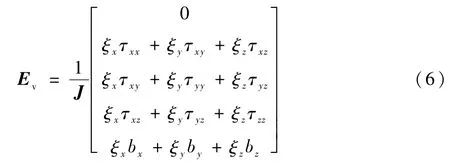
其中：τxx和bx分别为黏性力的切应力项和正应力项，下标标明各自不同方向上的分量。

J为笛卡儿坐标与一般坐标系间转换的Jacobian矩阵，即

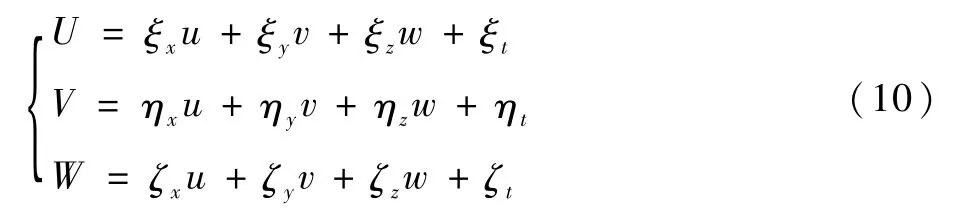
1.2 旋翼桨叶贴体网格

图1为SA349／2旋翼桨叶贴体网格，其旋翼采用3片OA209翼型的矩形高速桨叶，并具有一定的负扭转。本文对其桨根位置进行简化处理，在离散具有负扭转区域操作如下：提取三角面元网格的轮廓线得到桨叶叶素（剖面）线网格，对剖面线网格重布后，基于OversetGrid软件平移旋转操作，在线性负扭转桨叶段生成结构化面网格，若是非线性负扭转，取多段进行以上操作，对旋翼桨叶结构面网格进行重布，在桨尖和桨根位置加密。因此，桨尖和桨根位置应具有更多的重叠区域。

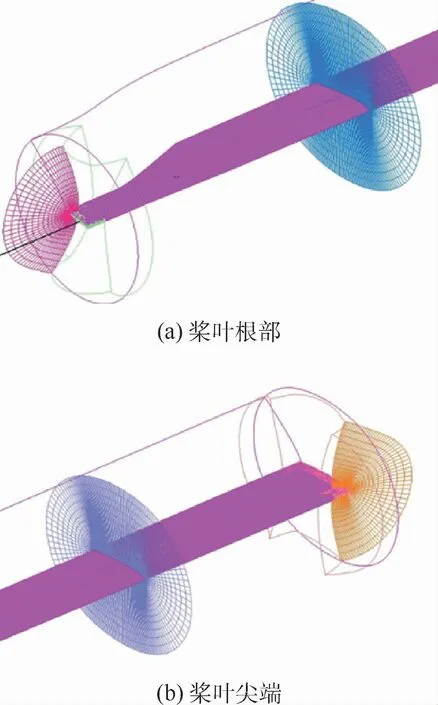
图1 SA349／2旋翼桨叶贴体网格Fig.1 Body-fitted grid of SA349／2 rotor blade

主体网格生成方法步骤如下：

步骤1 几何建模软件CATIA生成旋翼桨叶的几何模型，进而使用ICEM 或OversetGrid离散得到三角元桨叶表面网格。

步骤2 提取三角元网格的轮廓线，生成桨叶线网格，并重布线网格（重布线网格时，桨根桨尖的展向周向都需加密，以便生成合适的贴体帽子网格）。

步骤3 通过线网格生成桨叶表面结构化面网格，并在2个端面生成重叠嵌套的端面网格，称之为“帽子”网格；在表面网格的基础上采用Hyp.tangent体网格推进方法生成近体网格。

两侧帽子网格方法步骤如下：

步骤1 抽取桨叶主体面网格两端线网格，从而生成2个端面网格。

步骤2 提取主体面网格前缘后缘网格（提取的前、后缘网格节点数相同）。

步骤3 将步骤1、步骤2提取出的网格进行连接，并提取新生成的端面网格上下的线网格。

步骤4 指定主面网格为翼型结构化网格的参考面，以该参考面生成紧贴主面网格的新的面网格，并将其与新生成的端面面网格连接，从而形成帽子网格。

表1为网格规模，其贴体网格系统总数为1 150万。

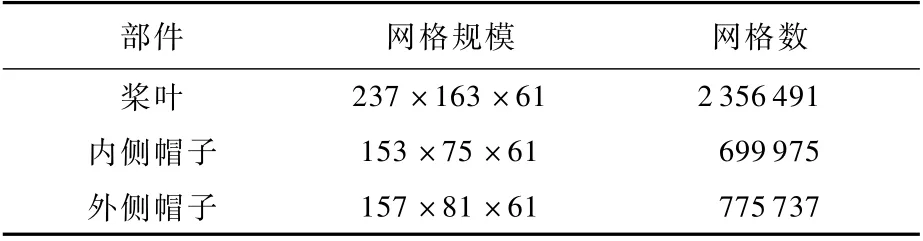
表1 SA349／2旋翼桨叶贴体网格规模统计Tab le 1 Num bers of body-fitted grid of SA349／2 rotor blade

1.3 旋翼桨叶背景网格

对于前飞状态，采用笛卡儿自动背景网格结合网格自适应，应用于动态计算，采用网格自适应功能时，网格数量会随着计算过程增加，故流场和压力系数曲线会更加光顺，对桨尖涡具有很好的捕捉能力，结果更加准确。

笛卡儿自动背景网格系统如图2所示，其部分剖面图如图3和图4所示。此背景网格共有9级，以应用于计算悬停状态。第1级背景网格（L1）由均匀网格间隔（Δ＝10%ctip）构成，其他“砖网格”（L2，L3，…）通过逐层增加到L1网格外围，迅速扩展到计算外场。计算外场尺寸为17倍旋翼半径，每一级别背景网格是上一级背景网格间隔的2倍，其中粗网格具有Δ2＝2Δ1，Δ3＝4Δ1，Δ4＝8Δ1，…；在网格自适应中，网格间隔具有类似关系式，Δ-1＝Δ1／2，Δ-2＝Δ1／4，…。对于L1网格，其尺寸和间隔由手动定义，旋翼的展向扩展为1.25R（R为旋翼半径），旋翼上方和下方扩展为0.3R，其第1级背景网格（L1）间隔仍取Δ＝10%ctip。

图2 SA349／2旋翼流场笛卡儿自动背景网格Fig.2 Cartesian automatic background grid of SA349／2 rotor flow field

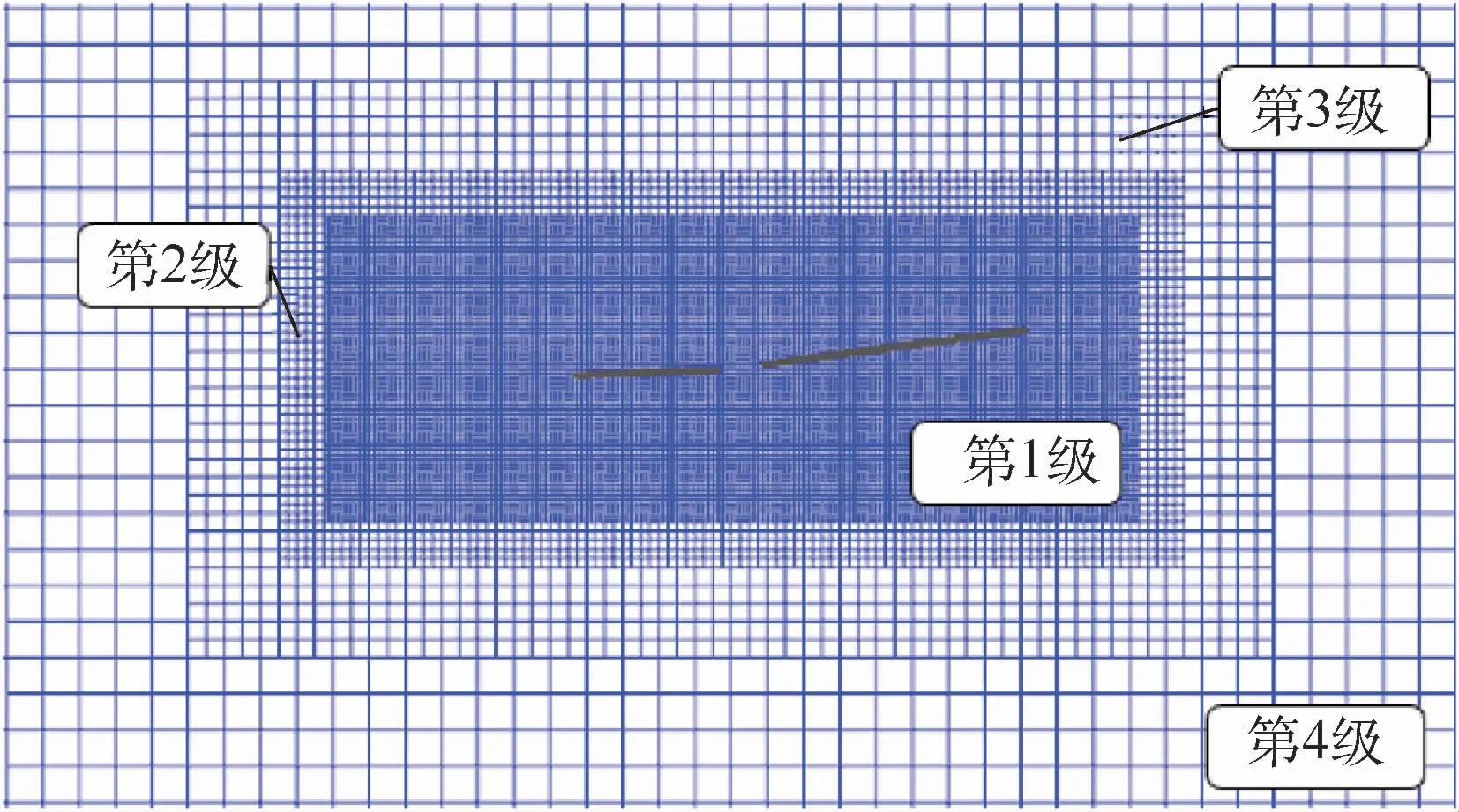
图3 适合前飞状态求解的笛卡儿自动背景网格剖面Fig.3 Cartesian automatic background grid section for solving in forward flight status

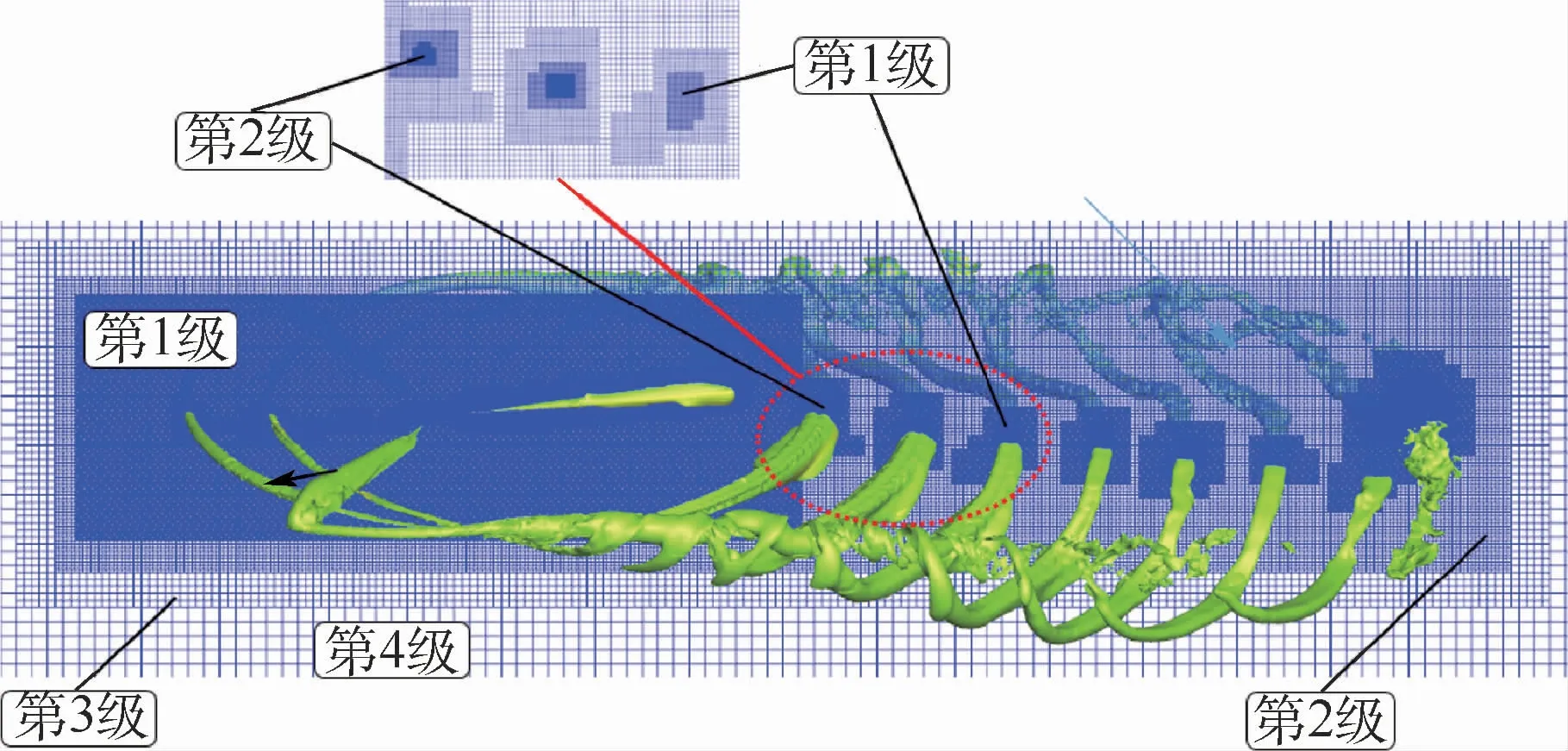
图4 旋翼前飞状态笛卡儿背景网格自适应Fig.4 Cartesian adaptive background grid of rotor for forward flight

笛卡儿第9级背景网格之间的间隔关系可表示为

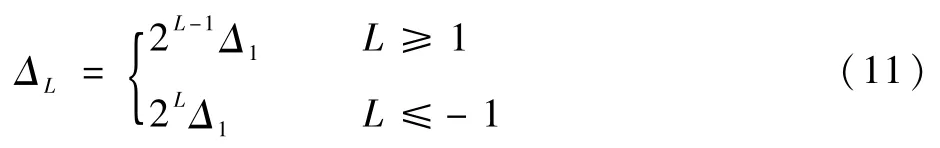
1.4 旋翼网格运动与变形

对于稳态飞行状态，旋翼桨叶的运动是在配平位置处的稳态周期响应，包括刚体运动和弹性变形。本文在对旋翼网格运动中分别施加旋翼桨叶的刚体运动和弹性变形，两者叠加实现桨叶真实运动。旋翼刚体运动通过GMP定义，弹性变形通过Motion（即旋翼旋转一周弹性变形关于方位角、桨叶展向位置的函数）文件来定义。驱动网格运动，更新网格位置，挖洞插值，循环直到计算模拟收敛，流程如图5所示。

旋翼桨叶刚体运动是指在工作过程中没有发生弹性变形。旋翼在绕旋翼轴旋转运动的同时，具有的挥舞、摆振、扭转运动可以设定为桨叶整体绕不同轴的单自由度转动，即绕挥舞铰的挥舞运动βb、绕摆振铰的摆振运动ζb及绕变距轴线的扭转运动θb。

为描述旋翼姿态及桨叶的刚体挥舞、摆振及扭转运动：

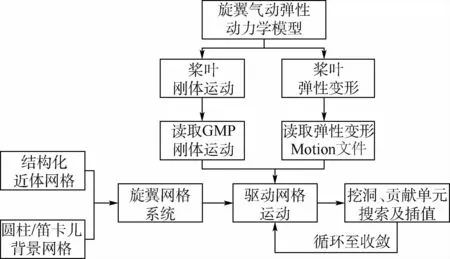
图5 旋翼网格运动与变形Fig.5 Motion and deformation of rotor grid

1）桨盘平面的姿态角。针对孤立旋翼情况，旋翼轴的几何前倾角与配平得到的机身姿态角可通过前处理软件OversetGrid调整网格位置实现，亦可在求解流场时在来流中定义。

2）单片桨叶组件（包括桨叶表面和2个端面网格）。网格刚体运动过程中，通过驱动组件运动实现网格运动，每片桨叶定义为一个组件，实现桨叶绕轴的转动和挥-摆-扭／操纵的运动，先定义铰偏置量，后定义挥-摆-扭／操纵的速率。

3）旋翼组件。定义旋转的转向和速率。同一旋翼的桨叶组件共同定义在一个“父”组件下。旋翼组件和每个单片桨叶之间存在相对运动，即桨叶组件随“父”组件旋转运动外，还均有自身的运动。

每个组件生成一组重叠网格，根据组件定义的运动更新其所对应的网格位置，再重新进行网格的挖洞和插值，并计算求解新的流场。桨叶的弹性变形处理为一维梁的运动，忽略剖面的翘曲，通过本文CSD模块计算桨叶的弹性轴运动，提取每个展向站点处3个方向的平动和转动，分别为拉伸位移、摆振位移、挥舞位移、扭转角、挥舞角、摆振角信息，以此表达桨叶剖面的运动；并表示成Motion文件，传递给CFD模块。

Motion文件中定义有第一片桨叶变距轴线信息，在CFD计算时，通过与网格信息的比较找到第一片桨叶位置，利用这些旋翼桨叶数据表，采用样条插值将数据传递给网格剖面，驱动剖面的变形运动，最终更新桨叶近体网格的位置，实现桨叶的弹性变形。

图6为通过Motion文件施加旋翼挥舞方向的变形，并与未变形桨叶对比。在网格变形后，仍通过挖洞、贡献单元搜索和插值计算旋翼流场。

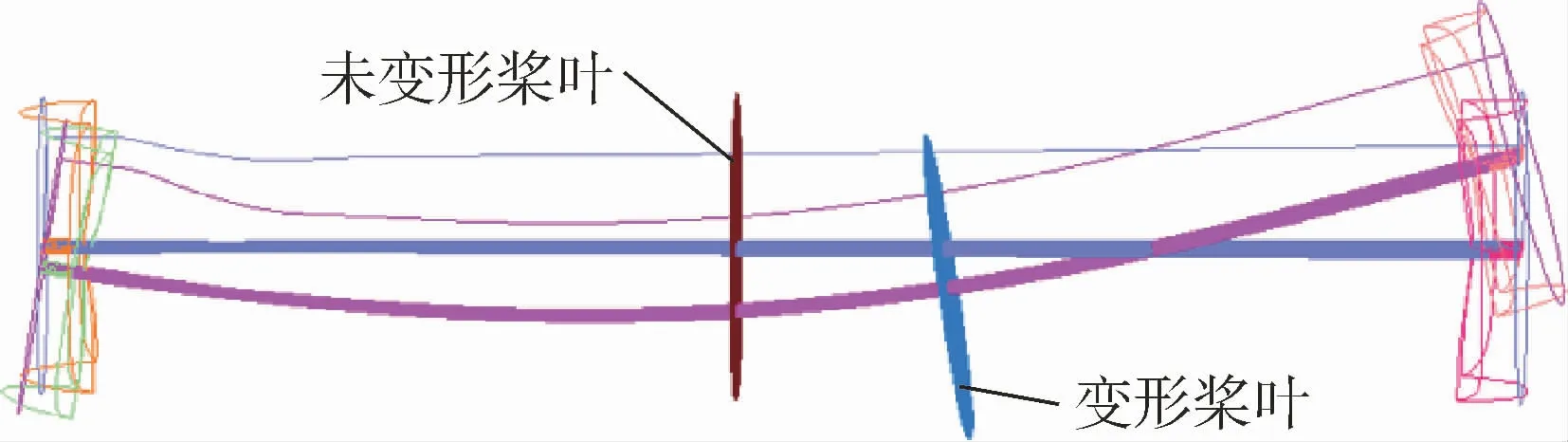
图6 桨叶弹性变形示意图Fig.6 Schematic of blade elastic deformation

2 旋翼气弹综合分析模型和CFD／CSD松耦合策略

本文基于Hodges和Dowell［12］建立的中等变形梁理论，运用Ham ilton原理推导旋翼桨叶的运动方程，以空间有限元方法［13］离散旋翼桨叶，运用模态叠加法和直接数值积分法建立直升机旋翼桨叶气弹综合分析模型［14］。

引入了CFD气动力修正的CSD模块计算流程如图7所示。

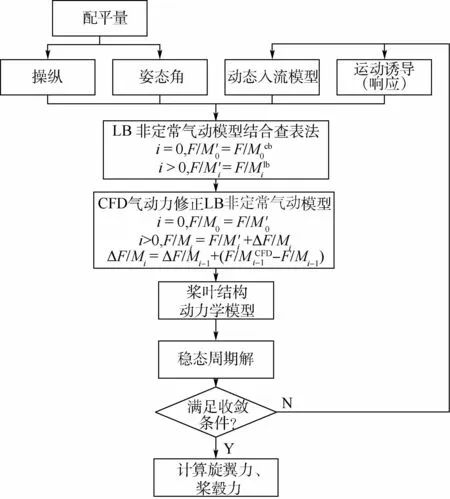
图7 CSD模块与CFD气动力耦合计算流程Fig.7 Flowchart of CSD／CFD aerodynamic force coupling calculation

图8为旋翼配平及耦合策略内外两层循环流程，耦合计算以CSD模块平台作为主控平台。启动计算，气动力借助查表法获得，计算旋翼力

对于第1（i＝1）次配平，运用LB非定常气动模型计算气动力，并采用上一圈CFD计算的气动力修正查表法。

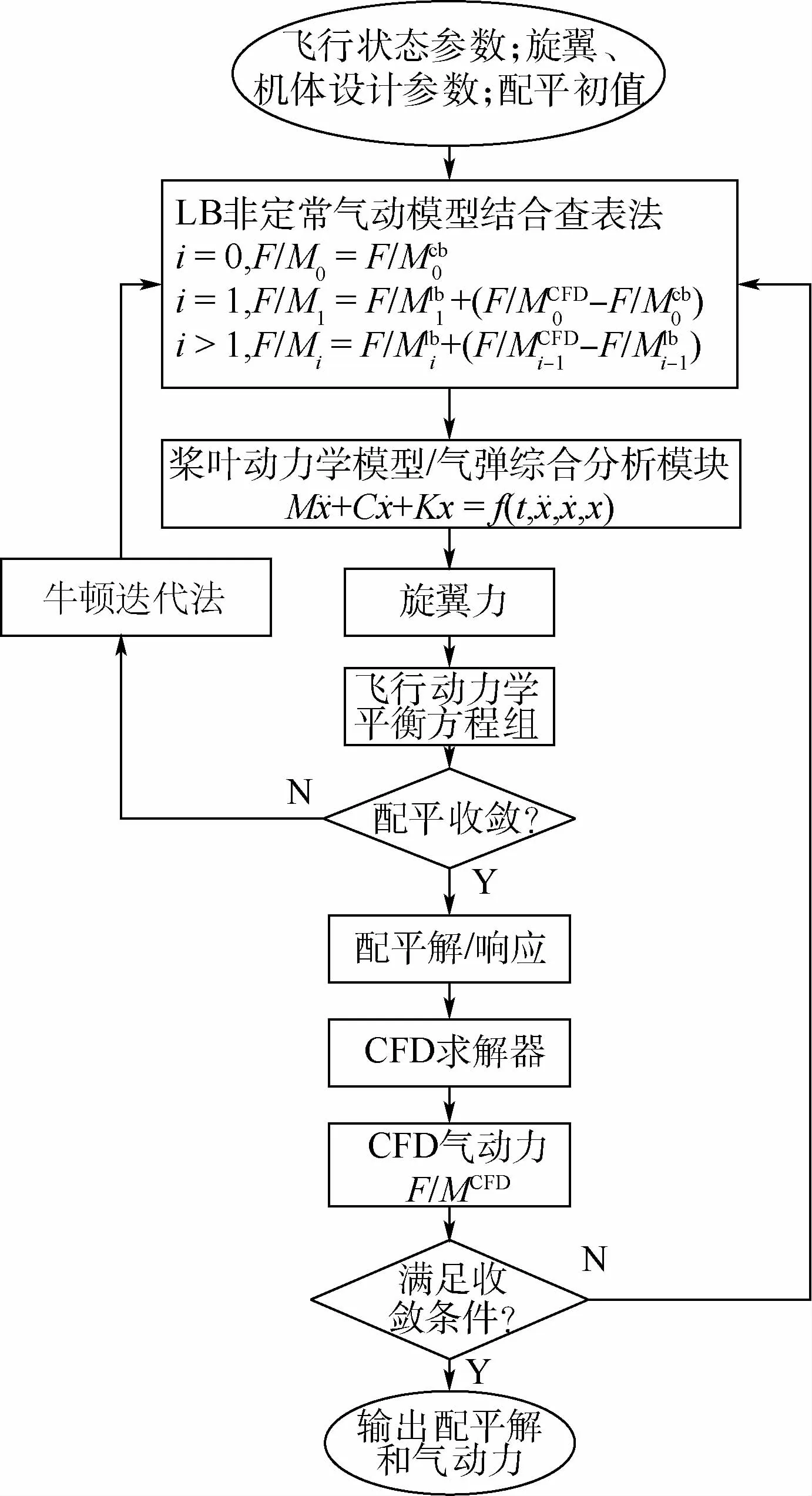
图8 旋翼配平及耦合策略内外两层循环流程Fig.8 Circulation flowchart of inner and outer loop for rotor trim and coupling strategy

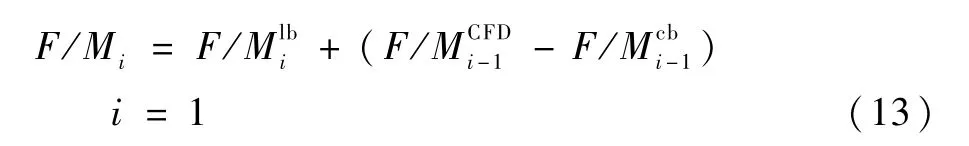
式中：上标lb表示运用LB非定常气动模型计算得到的旋翼气动力，CFD表示采用CFD技术得到的旋翼气动力。

对于第i（i＞1）次配平，使用上一圈CFD计算的气动力修正LB非定常气动模型。

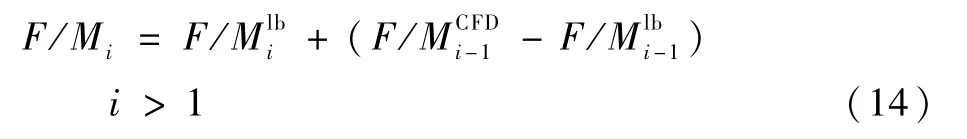
式（14）也可理解为第i-1次CFD气动载荷结果无法满足配平平衡方程组时，通过LB非定常气动模型结合查表法修正CFD计算结果使其满足配平方程组并求解得到配平解，即

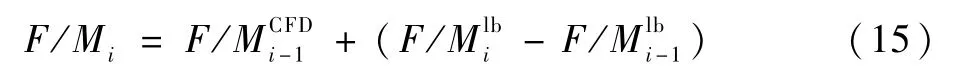
耦合计算通过使用OverCFD求解器及MATLAB编程的CSD综合分析程序进行，基于Linux平台，采用MPI并行计算协议。数据交换通过CFD求解器计算的剖面气动力文件及CSD模块计算的配平量和响应进行。为更好地理解整个耦合配平过程，下面将分条目阐述各个计算流程，并对环节中关键点进行阐述说明。详细配平耦合过程如下：

步骤1 启动计算，使用飞行力学解析配平的配平量为基础，作为CSD综合分析模型的初值来使用，基于动态入流模型、旋翼配平量和运动诱导，通过LB非定常气动模型结合查表法计算旋翼气动力F／M′0，结合梁模型和叶素理论，并采用有限元方法求解动力学方程解算结构响应并进一步计算旋翼力，将此旋翼力代入配平平衡方程组，以牛顿迭代法更新配平量，求解动力学方程组。输出旋翼操纵量、姿态角、刚体稳态响应及桨叶弹性变形，并以文件形式输出剖面马赫数分布和剖面力系数，供下次迭代使用。

步骤2 将旋翼总距、横／纵向周期变距、俯仰角、侧倾角及挥舞摆振的刚体运动通过GMP传递给OverCFD模块（俯仰角、侧倾角亦可通过来流设定），弹性变形通过Motion文件传递给Over-CFD模块。在CFD计算中，数值格式采用2阶中心差分格式，湍流模型采用SA模型，时间推进选择ARC3D Diag，限制器选用Koren，耗散项选择TLNS3D Diss，每步进行30次牛顿内迭代，初次CFD计算旋翼桨叶旋转1圈，输出旋翼桨叶各剖面的垂直力系数Cn、绕变距轴的力矩系数Cm、弦向力系数Cc在桨盘平面和桨叶展向的分布（F／，供CSD综合分析模块调用。

也可进行桨叶旋转1／Nb圈（Nb为桨叶片数）后计算所得各剖面气动力，无需保证每次迭代CFD计算气动力收敛，只需保证整个耦合过程是收敛即可。

步骤3 在CSD综合分析程序中，通过读取上次耦合迭代的CFD求解器计算气动力和CSD模块输出保存的气动力，并将两者做差，引入旋翼沿展向和周向各剖面气动力增量，即ΔF／M1。

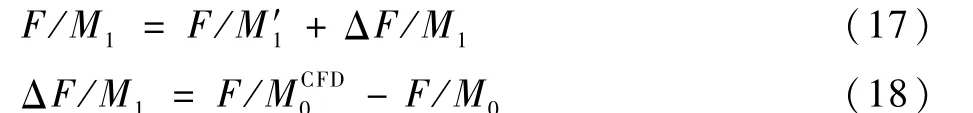
读取CSD综合分析程序上次迭代计算输出的配平量，作为程序启动值，计算新的配平量并输出下次迭代所需要的全部信息。

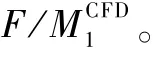
步骤5 重复步骤3中CSD综合分析模块，即可得到

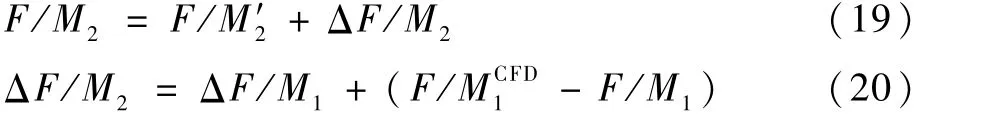
步骤6 循环步骤2～步骤5，当2次相邻迭代气动力收敛，即ΔF／Mi≈0，配平操纵和姿态角收敛，即视为耦合过程收敛。此时CFD模块、配平模块与气弹模块同时收敛，且

以上耦合流程可归纳为：在每次耦合迭代过程中通过ΔF／Mi来修正查表法得到的气动力，归纳式（12）～式（21）可得

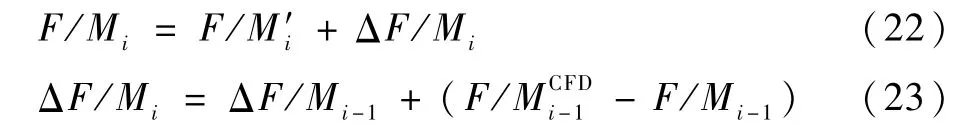
通过CFD模块和CSD综合分析程序求得气动载荷之差而引入增量ΔF／Mi，其在每次迭代过程中都做了更新。

3 算例验证

3.1 SA349／2直升机参数

本文选取SA349／2直升机稳态前飞的小速度状态（前进比为0.14）为算例，此状态具有明显的桨涡干扰现象。通过CFD／CSD耦合方法计算旋翼气动力，并观测流场现象，计算旋翼桨叶稳态响应和振动载荷，并将气动载荷和振动载荷计算结果与飞行实测进行对比，验证本文方法的有效性。

SA349／2直升机为铰接式旋翼构型，翼型采用OA209，图9给出文献［15］及本文使用的桨叶网格负扭转ψ分布。图中：r／R表示归一化半径。

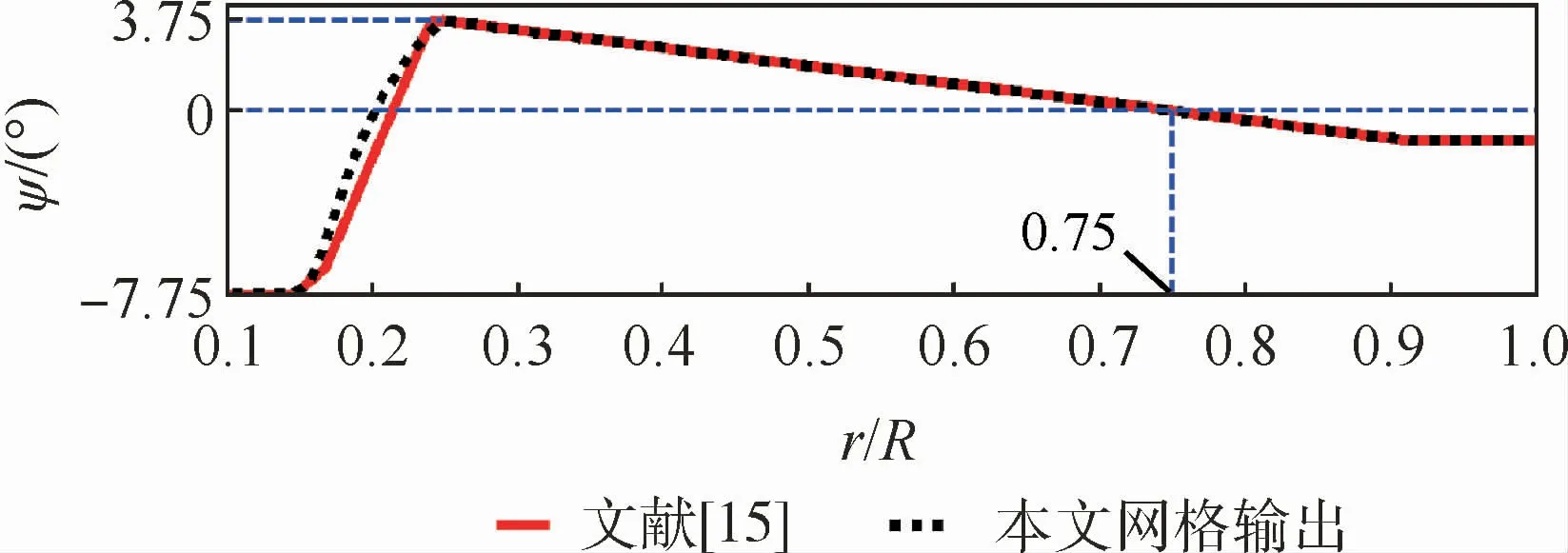
图9 SA349／2直升机桨叶负扭转对比Fig.9 Comparison of blade twist of SA349／2 helicopter

3.2 CFD／CSD松耦合计算结果

采用第2节阐述的耦合策略进行的配平计算具有较好的收敛速度，CFD模块与CSD综合分析模块耦合4～5次，所得气动力即可收敛，得到的垂直力系数与实测值［15］具有较好的一致性；且输出的气动载荷同样捕捉到了桨涡干扰现象，进一步反映出本文方法的有效性。表2为此状态的配平解。

图10为桨叶剖面（r／R＝0.75，0.97）处的垂直力系数与实测值随配平耦合历程的对比情况。图中：实线为配平迭代过程每次循环CFD仿真计算的气动载荷，虚线为通过配平程序在采用第2节中阐述的耦合策略输出的气动载荷。

表2 SA349／2直升机飞行状态2［15］的配平解Table 2 Trim solution of SA349／2 helicop ter in flight status 2［15］ （°）

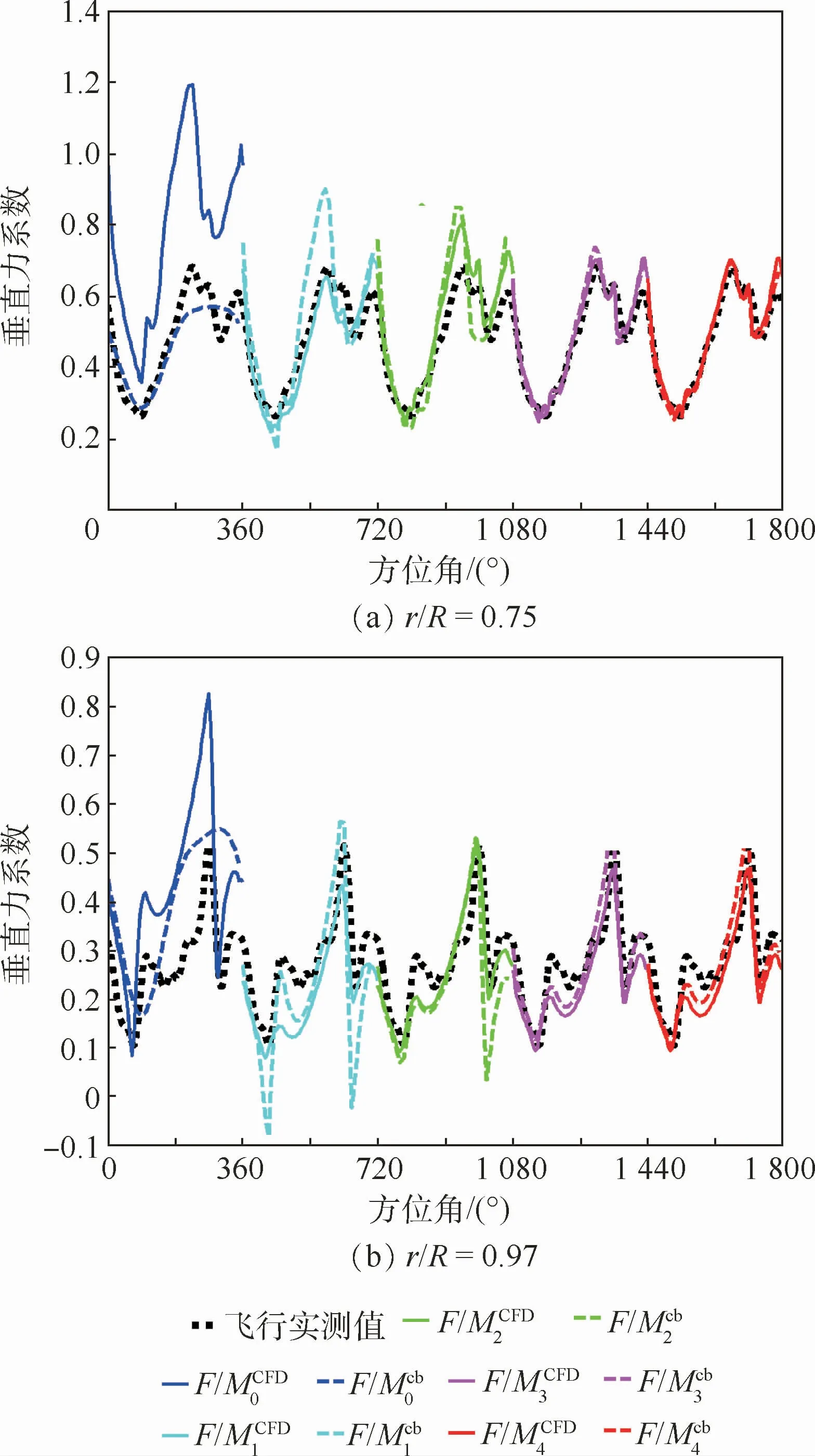
图10 桨叶剖面配平历程Fig.10 Blade section trimming process

图11给出了CFD／CSD耦合计算收敛后剖面垂直力系数的本文结果、飞行实测值及文献分析结果的对比。图中：基于文献配平解的CFD计算是指使用文献［15］给出的配平操纵量及响应计算的刚体模型气动载荷，CFDc815指第5次耦合计算CFD输出的气动载荷，配平c815指第5次耦合计算配平模块输出的气动载荷，均匀入流模型、预定尾迹模型及自由尾迹模型数据取自CAMRAD［16］计算值。

从图11（a）可以分析得出，对于r／R＝0.75特征剖面，CFD／CSD耦合计算值与飞行实测值具有很好的一致性。CFD／CSD耦合计算方法计算的垂直力较CAMRAD具有更好的精度，在本文方法中，每次配平计算通过查表法及引入ΔF／Mi增量的方法得到新的配平气动载荷，同样很好地捕捉到桨涡干扰现象，且与飞行实测值相比具有较好的计算精度。而基于文献［15］配平解得到的CFD气动力，配平位置与飞行实测值相比过高。

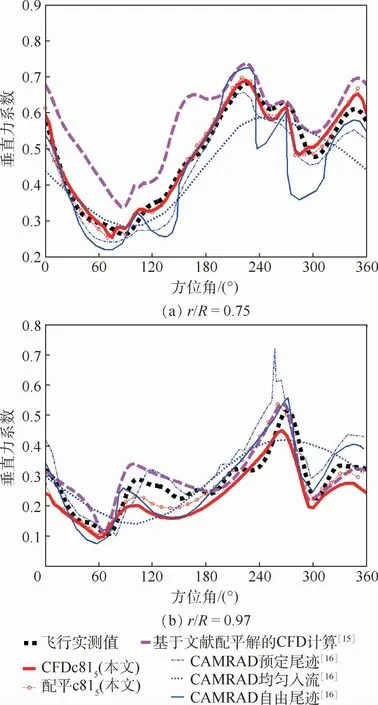
图11 低速飞行状态桨叶剖面垂直力系数对比Fig.11 Comparison of vertical force coefficient of blade section in low-speed forward flight

从图11（b）可以分析得出，CFD／CSD松耦合计算的垂直力系数与飞行实测值有一定的差距，而基于文献配平解的计算与飞行实测值具有较好的吻合度，可能是本文的CFD仿真计算未充分考虑机身影响，耦合过程机身和安定面气动载荷取自文献［15］的拟合值，可能存在一定误差。

在低速飞行状态下，旋翼的桨涡干扰效应对气动载荷具有极大的影响。从图10和图11可以看出，桨尖涡诱导产生的不均匀入流可导致较为突出的气动载荷，其中桨尖位置受桨涡干扰尤为显著。桨尖涡向桨叶内测移动，在前行桨叶90°方位附近造成桨尖气动载荷突增，出现“下-上脉冲”；涡向桨尖移动，在后行桨叶270°方位附近造成桨尖气动载荷突降，出现“上-下脉冲”。对于桨涡干扰现象，低速飞行状态尾迹涡计算的涡量图可以得到很直观的反映。

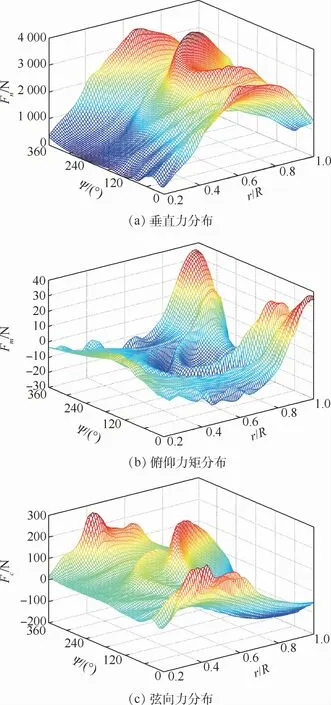
图12 低速飞行状态桨叶剖面垂直力、俯仰力矩和弦向力分布Fig.12 Distribution of blade normal force、pitching moment and in-plane force coefficient in low-speed forward flight

图12给出了SA 349／2直升机小速度稳态前飞状态旋翼桨叶剖面垂直力Fn、俯仰力矩Fm和弦向力Fc随展向和周向的分布情况。从图12（a）中可以直观看出，在方位角Ψ为90°和270°附近、桨尖段的桨涡干扰现象在桨叶展向r／R＝0.75处垂直力达到峰值。

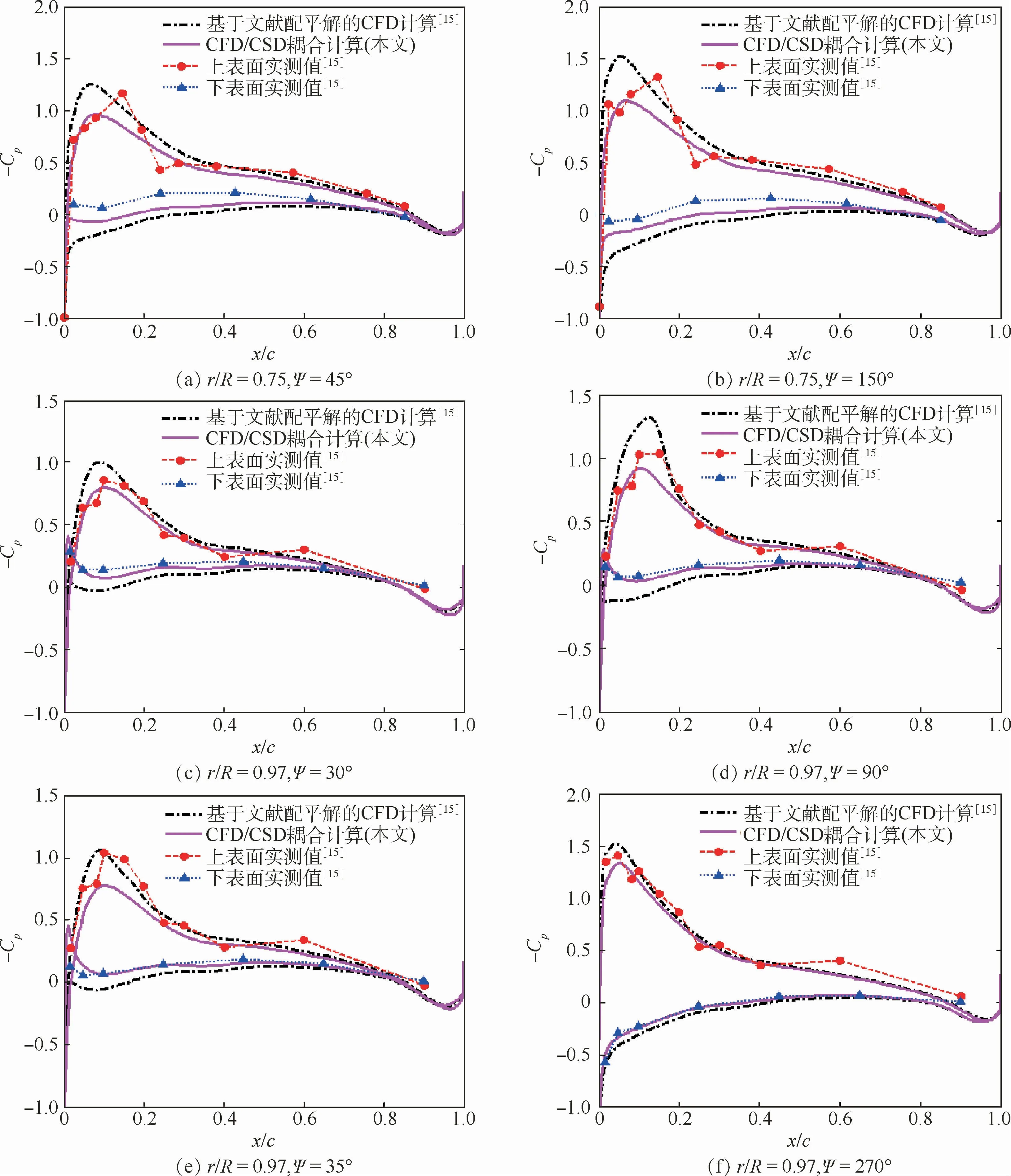
图13 低速飞行状态桨叶剖面压力系数对比Fig.13 Comparison of blade surface pressure coefficient in low-speed forward flight

图13为小速度稳态前飞状态，通过CFD／CSD耦合方法、飞行实测值及基于飞行实测操纵和响应的CFD计算值，桨叶剖面处压力系数的对比。图中：-Cp、x／c分别为压力系数负值、归一化弦向位置；基于文献配平解的CFD计算指用文献［15］中给出的配平量来进行CFD计算所获的结果；CFD／CSD耦合计算指本文计算值；上／下表面实测值指文献［15］中给出的桨叶表面压力系数实测值。通过曲线对比不难发现，对于下表面压力系数，本文方法的计算值明显与飞行实测值吻合更好。对于上表面压力系数，本文方法的计算值略低于飞行实测值，尤其r／R＝0.97剖面在90°和135°方位角的计算值，可能是桨涡干扰的影响，造成部分位置计算结果误差。总体来讲，通过本文方法计算的压力系数分布与实测值具有较好的一致性，验证了本文方法的有效性，且对计算旋翼稳态前飞状态气动力及流场具有很好的精度。对于计算结果的误差，因为本文建立的网格是对真实桨叶的简化，桨叶网格不准确可能带来误差；此外，CFD求解器未考虑低速预处理也可能导致压力系数不精确。

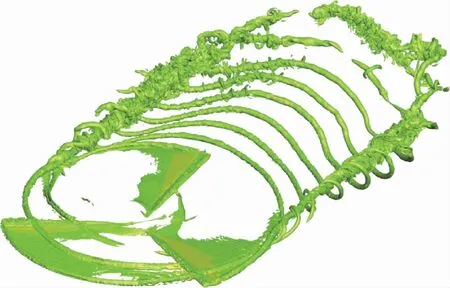
图14 低速飞行状态笛卡儿自动背景网格自适应计算旋翼涡量等轴视图Fig.14 Rotor vorticity isometric view of Cartesian automatic background grid in low-speed forward flight

图14为通过本文方法求得的旋翼涡量图。可以看出，本文方法对旋翼桨尖涡及桨涡干扰现象具有很好的捕捉能力。

4 结 论

1）本文建立的CFD／CSD松耦合策略能有效将基于CFD方法的高保真气动力引入到气弹综合分析模块中，有效提高气动力模型精度的同时兼顾时间效率。

2）本文建立的CFD／CSD松耦合配平计算方法可有效地用于直升机前飞状态下的全机配平分析，并具有良好的精度、收敛性和稳定性。

3）本文改进的耦合分析策略对计算旋翼稳态前飞状态气动力及流场的计算具有很好的精度，能有效捕捉到桨涡干扰现象等现象，为高精度的气弹响应和载荷分析奠定了良好的基础。