基于光场成像技术的散射性火焰温度场重建
黄兴,齐宏,*,牛志田,任亚涛,阮立明
(1.哈尔滨工业大学 能源科学与工程学院,哈尔滨150001; 2.空天热物理工业和信息化部重点实验室,哈尔滨150001)
高温燃烧广泛存在于航空航天、能源动力、钢铁冶金、化工等领域,发动机、燃气轮机、内燃机等高温设备中均存在燃烧现象。火焰作为燃料燃烧时生成的剧烈的光热现象,其温度场直接表征了燃烧的状态,如燃烧的稳定性、燃烧效率、反应速度、火焰三维结构等。准确测量燃烧过程中火焰的温度分布,不仅可以更好地认识燃烧产物的生成机理与火焰中的热量传递和吸收过程,还可以为生产设备的安全运行、燃料热能的充分利用及燃烧污染物的有效控制提供数据支撑。如在航空发动机的设计中,燃烧室出口温度是一项很重要的设计参数,可作为衡量发动机性能的一项重要指标,对其温度进行测量可为发动机设计提供参考。因此,对火焰空间测温技术的研究有十分显著的现实意义。
目前,常用的测温手段主要分为接触式测量和非接触式测量2类。对于接触式测量,测温元件需要接触火焰,这会导致火焰流场受到干扰,且接触式测量为点测量方式,无法实现整个温度场的测量。近年来,基于辐射成像的火焰测温技术受到了国内外学者的广泛关注[1-3]。该方法具有非侵入式、无需外加激励源等优点,而且可以通过图像记录整个火焰辐射场的信息,进而实现场参数的重建[4-7]。根据成像元件的数量,辐射成像测温法可以分为单相机和多相机2类。单相机系统结构简单、易于实现,但由于成像角度受限,难以实现复杂形状火焰温度场的测量;多相机系统是在火焰周围不同位置和角度布置多个相机进行同时成像,以获得多个角度的辐射图像[8-10],该系统空间分辨率高,但是系统复杂成本高,而且操作更为繁琐。2005年,斯坦福大学的华裔学者Ng等[11]将光场成像的理论和技术应用于商业化,也为火焰辐射成像测温法提供了新思路。光场相机内部特有的微透镜阵列结构,可以通过单相机一次曝光记录全场的辐射光场信息,包括辐射强度的大小、位置及角度。该技术具有高的时间和空间分辨率,可以解决单相机采样角度有限及多相机系统复杂操作困难等一系列问题,因此基于光场成像技术的高温火焰温度场测量技术是一种非常有应用前景的测温手段[12-14]。
基于辐射成像的高温发光火焰温度场重构问题,从本质上是根据边界辐射强度分布求解辐射传输体系中温度场的问题,这是一个典型的辐射反问题。许多学者开展了有关重构模型与方法的研究。2002年,周怀春等[4]利用改进的Tikhonov正则化方法在CCD相机获取的火焰图像中重建出三维温度场,并证明了改进的Tikhonov正则化方法具有强的抗测量误差能力。2009年,黄群星等[5]采用立体适配器在一个高分辨率相机成像面上获得不同探测角度的火焰图像,充分利用了相机的分辨率,采用最小二乘QR(LSQR)分解算法和双色法实现了非稳态火焰断面二维温度和烟黑颗粒体积分数同时重建计算,得出了火焰断面的重建结果。2010年,刘冬和岑可法等[15]采用LSQR算法结合反向蒙特卡罗法实现二维、三维炉内温度场的反演,基于该方法,进一步采用8台CCD相机对300MW 煤粉炉炉膛的火焰温度分布进行了重建,获得了不同高度截面上温度分布规律[16]。2012年,刘冬等[17]在LSQR算法与截断奇异值分解算法(TSVD)的基础上,结合遗传算法(Genetic Algorithm,GA)构造了2种混合优化算法,利用GA的随机搜索能力减弱非最优正则化参数对于重建精度的影响。2014年,娄春等[18]利用Tikhonov正则化和广义截断奇异值分解的混合算法(TR-GSVD)重建了炉内的三维温度分布,并指出在重建过程中需要更新正则化参数。2016年,周怀春等[10]利用修正的Tikhonov正则化方法重建出了超临界锅炉炉膛内部的温度分布。目前,虽然大量学者针对辐射成像温度场重构问题开展了工作,但仍少有关于基于光场成像的火焰温度场重建反问题的报道。本文主要在光场成像及火焰辐射传输模型的基础上,开展吸收散射性火焰温度场重建算法研究,将Landweber算法应用到基于光场成像的火焰温度场重建,以具有较高计算精度的广义源项多流法作为正问题模型,采用Landweber算法作为反问题求解算法,根据光场成像模型模拟获得吸收散射性介质的辐射强度光场图像,据此重构出其三维温度分布。同时将在辐射成像测温中广泛应用的LSQR算法引入到本文研究中,作为对比以检验Landweber算法的性能。
1 光场成像及火焰辐射传输模型
1.1 光场成像模型
对于基于光场成像的高温火焰温度场重建问题,首要问题是建立准确可靠的成像模型以从拍摄得到的光场图像中提取全场的辐射强度分布。光场相机的内部结构如图1所示。与传统相机不同,在光场相机中,主透镜和传感器之间加装了微透镜阵列。火焰上一点发出的若干采样光线在经过主透镜之后汇聚于主透镜像面上的一点,再被微透镜阵列分散成若干束投射到不同的传感器像素上。每个像素上的采样光线方向信息可由像素和与之对应的微透镜确定,而其强度信息可通过图像的灰度值确定。
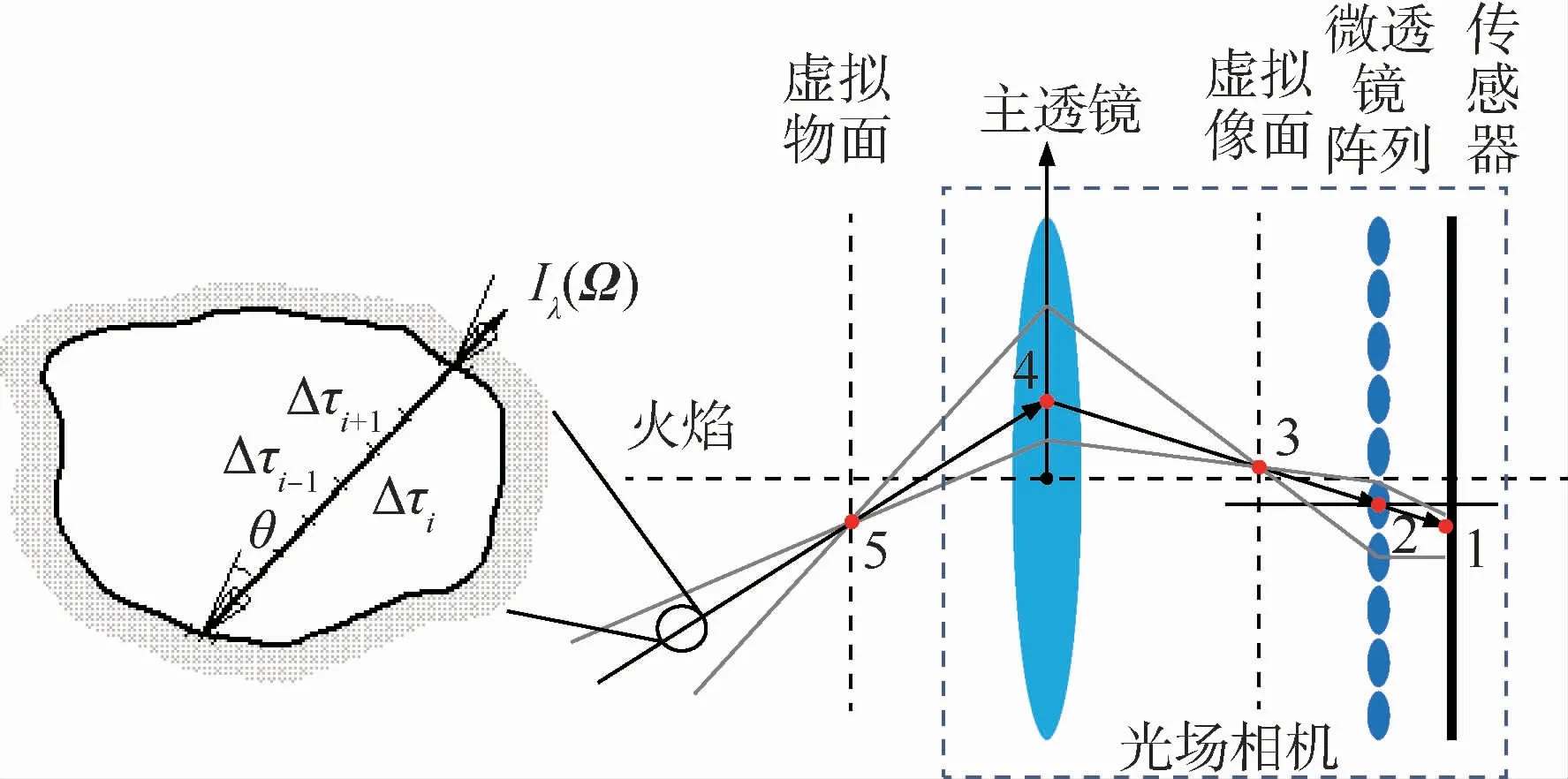
图1 光场成像的射线追踪示意图Fig.1 Schematic diagram of ray tracing of light-field imaging
根据式(1)和式(2)所示的透镜成像公式,可从像素点开始对采样光线进行追踪。

式中:sv为透镜的物距,s为透镜的像距,F为透镜的焦距。对于主透镜来说,sv为主透镜与虚拟物面之间的距离,s为主透镜与虚拟像面之间的距离,xv为光源点的坐标,x为对应的虚拟像点的坐标,F为主透镜的焦距;对于微透镜来说,sv为微透镜阵列与虚拟像面之间的距离,s为微透镜阵列与探测面之间的距离,xv为虚拟像点的坐标,x为与之对应的像素点的坐标,F为微透镜的焦距。因此,当光场相机的结构参数已知时,可以根据式(1)和式(2)计算得到光线的位置信息,即光线经过各个平面的坐标。
在获得各点的坐标后,可以根据各点的连线得到光线的方向信息。对于图1所示的采样光线,其在火焰内的传输方向可以根据点4和点5的连线得到。

式中:θ和φ分别为天顶角和圆周角。
基于上述光场成像模型,可以从光场相机拍摄到的光场图像中获得火焰边界上的出射辐射强度的位置、方向和强度信息,为基于光场成像的火焰温度场重建提供测量信号。
1.2 火焰辐射传输模型及算法
在通过光场图像获得火焰出射辐射强度信号之后,还需要建立出射辐射强度与火焰内部辐射强度之间的联系,才能实现火焰内三维温度场重建。火焰是一种典型的参与性介质,边界上的出射辐射强度是其内部各点辐射强度的累积。火焰内的辐射传输过程可以用如下辐射传输方程来描述:
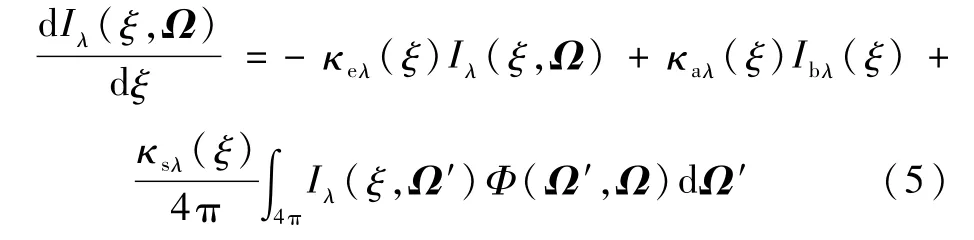
式中:Iλ(ξ,Ω)为介质在ξ位置处Ω 方向上的光谱辐射强度,W/(m2·μm·sr);Ibλ(ξ)为介质在ξ位置处的自身黑体光谱辐射强度,W/(m2·μm·sr);κeλ(ξ)为衰减系数,m-1;κaλ(ξ)为吸收系数,m-1;κsλ(ξ)为散射系数,m-1;Φ(Ω′,Ω)为Ω′方向入射并向Ω 方向散射的散射相函数。等号右侧第二项和第三项均可以使辐射强度增强,因此将二者之和定义为广义源项Sλ(ξ,Ω),即
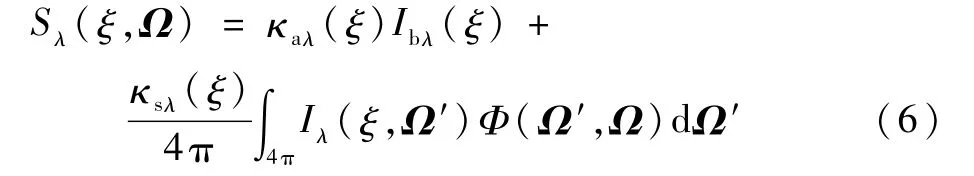
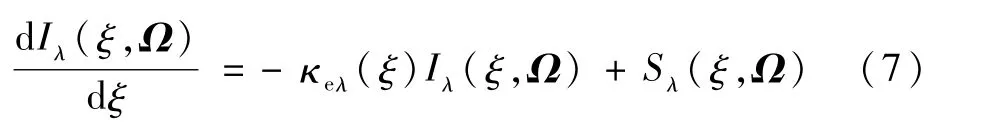
此时式(5)可以简化为可以看出,若源项已知,则可将式(5)所示的积分微分方程简化为式(7)所示的纯微分方程,进而可以通过沿程积分求解出火焰某一方向上的出射辐射强度。广义源项多流法就是在这种求解思路的基础上建立的。强度求解的关键在于对广义源项的求解。本文利用有限体积法(Finite Volume Method,FVM)计算火焰的广义源项。首先采用FVM求解较少离散方向上的辐射强度,从而根据式(6)获得火焰内的广义源项分布,根据广义源项的不变性[19],增加了离散角度之后广义源项的数值不发生改变,因此可以利用计算得到的广义源项计算出更多离散方向上的辐射强度。如图1所示,将Ω方向上探测线经过的火焰区域离散为N个网格,对式(7)在微元控制体内积分,可以得到

式中:κa为介质吸收系数,m-1;κs为介质散射系数,m-1;Ibi为控制体i自身黑体辐射强度,W/(m2·μm·sr);τi为探测线穿过网格的光学厚度;为控制体i在离散方向sj上的辐射强度值;ΔΩj为控制立体角;Ii+1(Ω)为穿过第i个网格后的辐射强度。因为火焰温度远高于周围环境温度,所以忽略环境辐射影响。假设每个网格内温度均匀分布,则Ω方向上的火焰边界出射辐射强度可由积分得到,其离散形式可表示为
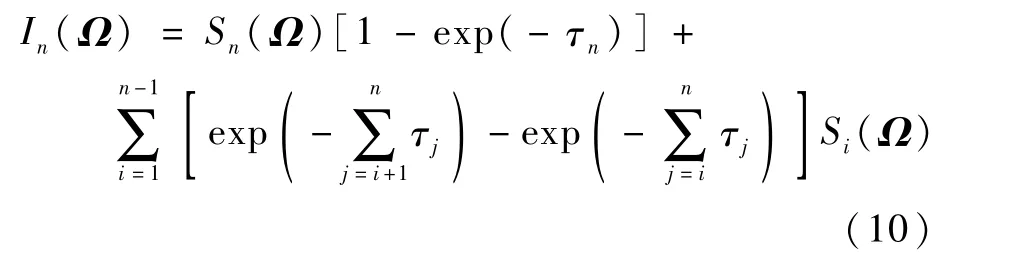
沿不同的探测方向对火焰内的辐射传输过程进行积分,可以得到火焰边界上的出射辐射强度分布,将其写成矩阵形式可表示为

式中:Aλ为衰减系数矩阵;Sλ为广义源项向量;Iλ为出射辐射强度向量,即光场相机最终接收到的辐射强度分布。
2 温度场重建算法
基于光场成像的火焰温度场重建,即根据由光场相机拍摄到的火焰光场图像获得火焰边界上的出射辐射强度分布,进而利用该出射辐射强度分布由火焰内的辐射传输模型重建出火焰的三维温度场。当辐射特性参数已知时,式(11)中的未知数仅为广义源项Sλ,可以将其视为线性方程组,通过求解式(11),可得到火焰内的源项分布。由式(6),火焰的自身黑体辐射强度包含在广义源项中,当源项已知时,利用FVM 可以计算出火焰内各点的辐射强度,进而计算出火焰的自身黑体辐射强度项,根据普朗克定律,待重建的温度场可以由火焰的自身黑体光谱辐射强度Ibλ计算得到,据此可实现火焰三维温度场的重建。
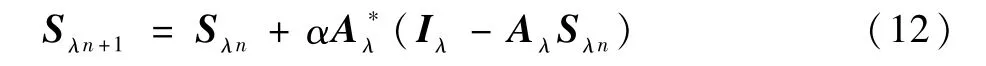
对于式(11),考虑到其系数矩阵Aλ是一个大型的稀疏矩阵,且问题本身具有非适定性,本文利用Landweber算法来求解方程组。对于式(11)所示的方程组,Landweber算法的求解格式如下:式中:α为松弛因子;A*为A的转置矩阵。Landweber算法适用于求解大规模不适定问题,方法较为稳定,即使在测量值存在噪声的情况下利用该算法也可以得到合理的解。但是传统的Landweber算法迭代序列收敛速度很慢,为了加速收敛,本文采用了一种改进的迭代格式[20]:

式中:a≥2为给定的正整数;E为单位矩阵;M 为过渡矩阵;n为迭代步数。虽然式(13)迭代一步的计算量要大于式(12),但是计算过程中总的迭代步数会大大减少。式(13)迭代k步,相当于式(12)迭代ak步,因此该迭代格式会大大提高算法的效率。在本文中取a=4。
基于光场成像与Landweber算法的火焰温度场重建流程如图2所示。
此外,为了衡量Landweber算法性能的优劣,本文还利用LSQR算法重建火焰的三维温度场以作为比较。该方法已被广泛应用于基于辐射成像的火焰温度场重建问题中,并被证明具有很高的重建精度。基于LSQR算法的火焰温度场重建流程与基于Landweber算法相似,在此不做赘述。
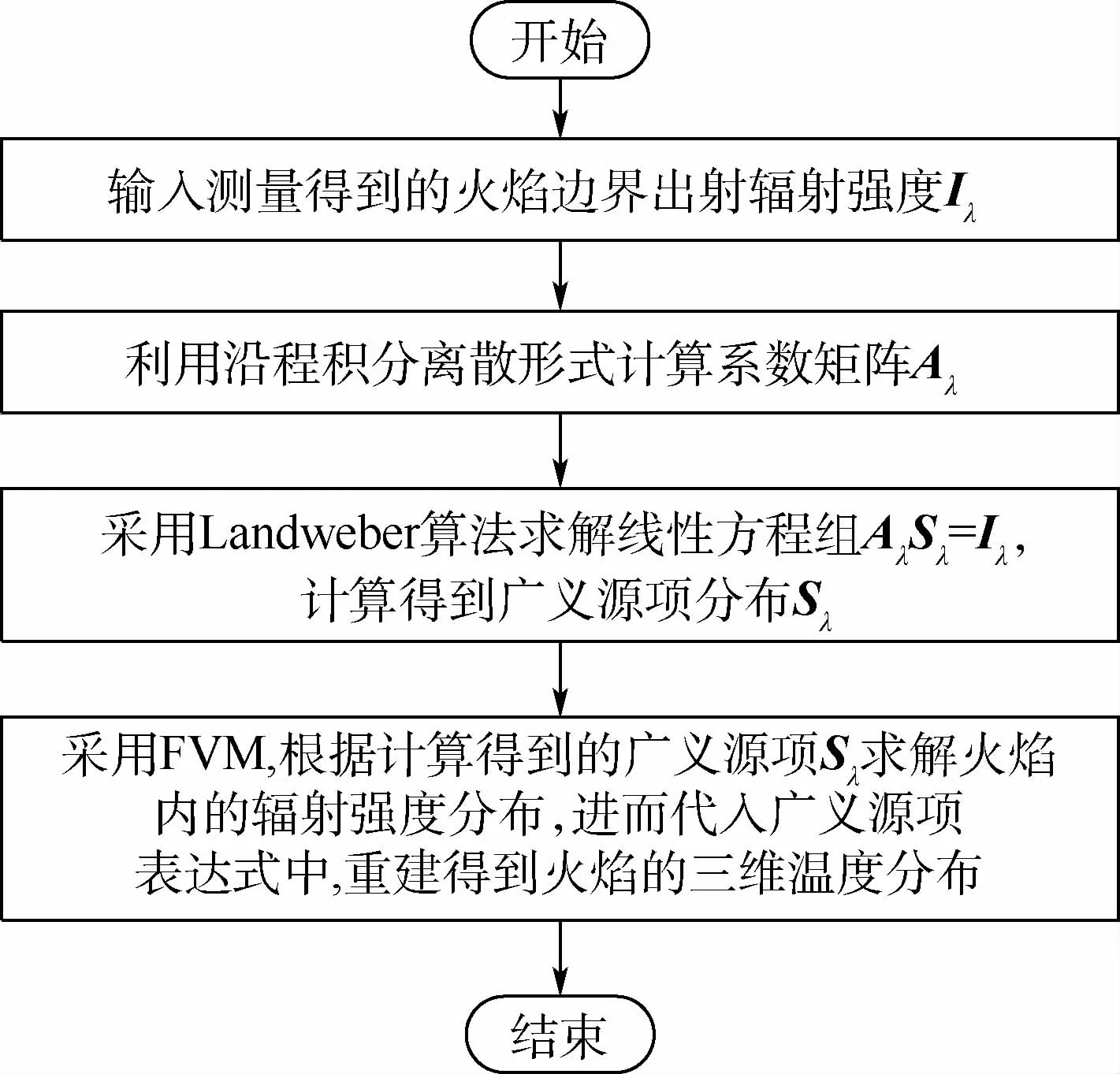
图2 基于光场成像与Landweber算法的火焰温度场重建流程Fig.2 Flowchart of flame temperature field reconstruction based on light-field imaging and Landweber algorithm
3 数值模拟结果与分析
在第1节成像理论模型的基础上,开展数值模拟计算来检验算法的性能。考虑一圆柱型介质,介质半径为0.05 m,高度为0.4 m,假设温度分布为轴对称分布。
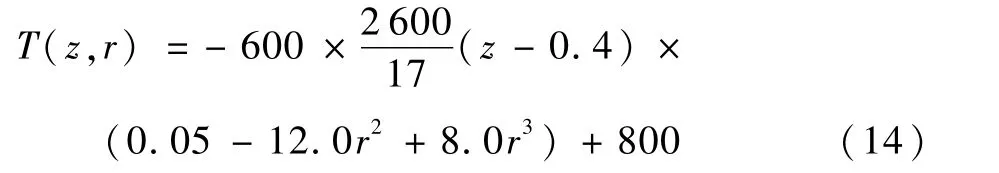
式中:z和r分别为轴向和径向坐标。假设火焰的吸收系数为3m-1,散射系数为3m-1。在圆周角、半径和轴向高度方向上将重建区域划分为Nφ×NR×NL=1×20×20个网格。
为了使模拟的辐射强度信号更贴合实际情况,在模拟的强度信号基础上添加随机测量噪声,如下:

式中:为一个满足标准正态分布的随机数;σ为添加噪声的标准差;Imea和Iexa分别为强度信号的测量值和精确值;γ为测量误差。
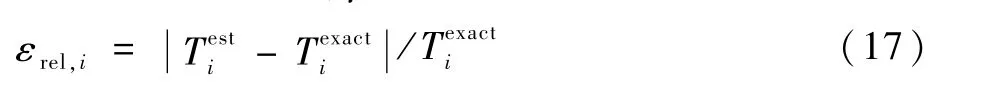
式中:εrel,i为单元网格温度重建值与真值的相对误差;为单元网格重建值;为单元网格的真实温度值。温度重建结果的平均相对误差为

利用上述光场成像模型模拟构建了介质边界辐射强度分布的光场图像,如图3所示。模拟研究中采用的光场相机结构参数见文献[21]。

图3 模拟光场图像Fig.3 Simulated light-field image
分别利用Landweber算法,LSQR算法对火焰温度场进行重建。为了研究测量误差对重建精度的影响,分别添加了1%、3%、5%的测量误差γ。不同测量误差情况下2种算法的重建结果如图4和图5所示(图中:R为半径,Z为高度),纵截面上的重建相对误差分布如图6和图7所示,平均重建相对误差及计算时间对比如表1所示。
从图4和图5中可以看出,在添加测量误差很小(小于3%)的情况下,采用2种算法重建出的温度分布均十分接近于假定的温度场分布;当测量误差逐渐增大时,重建结果中出现了抖动,温度场轮廓逐渐变得不规则,尤其是在添加了5%测量误差的情况下,在介质顶部位置有了较明显的波动。但从整体上看,重建的温度分布仍然清晰可见,且与真值相近,因而结果仍然是合理的。
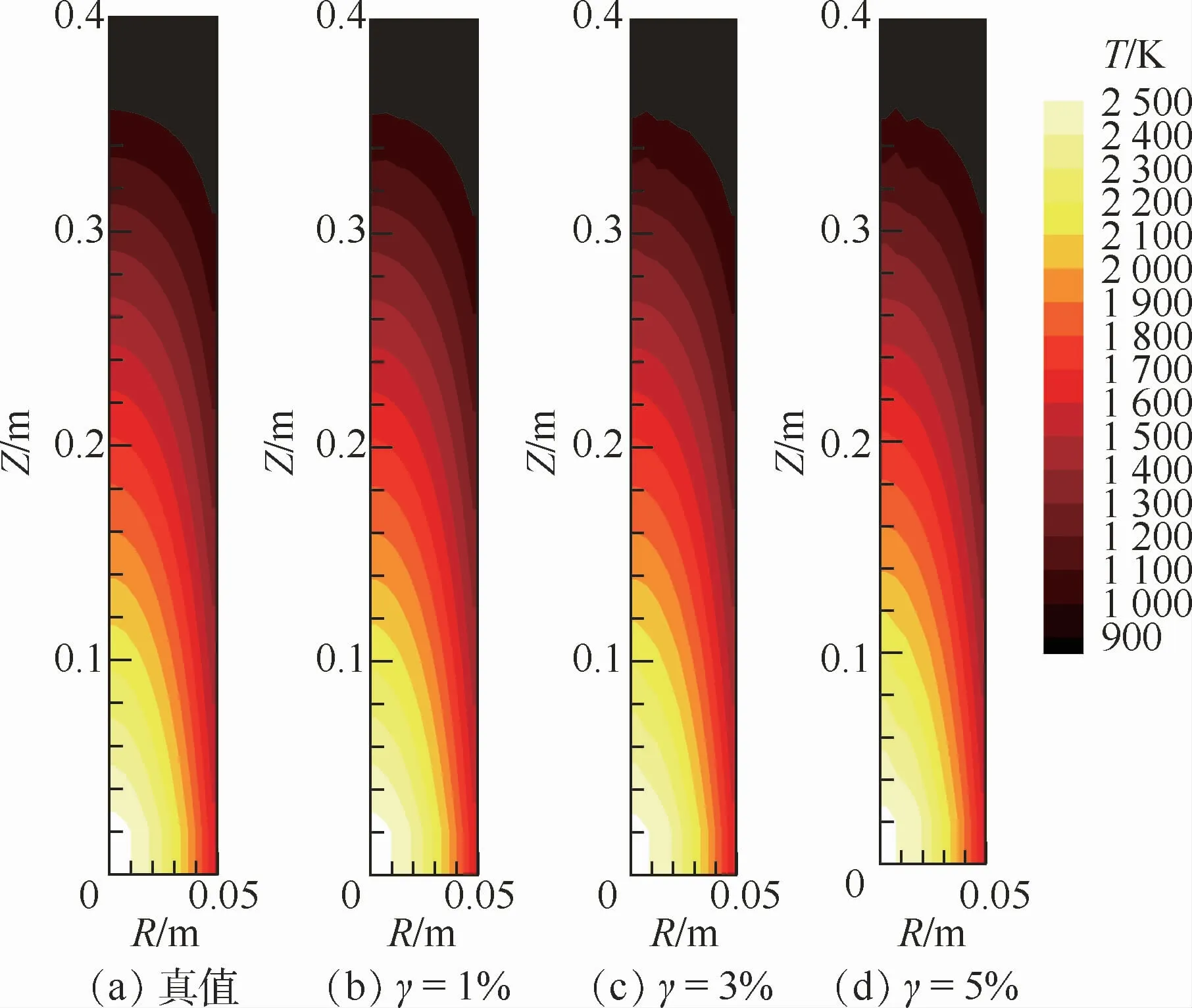
图4 LSQR算法三维温度场重建结果Fig.4 Reconstructed 3D temperature field distribution using LSQR algorithm
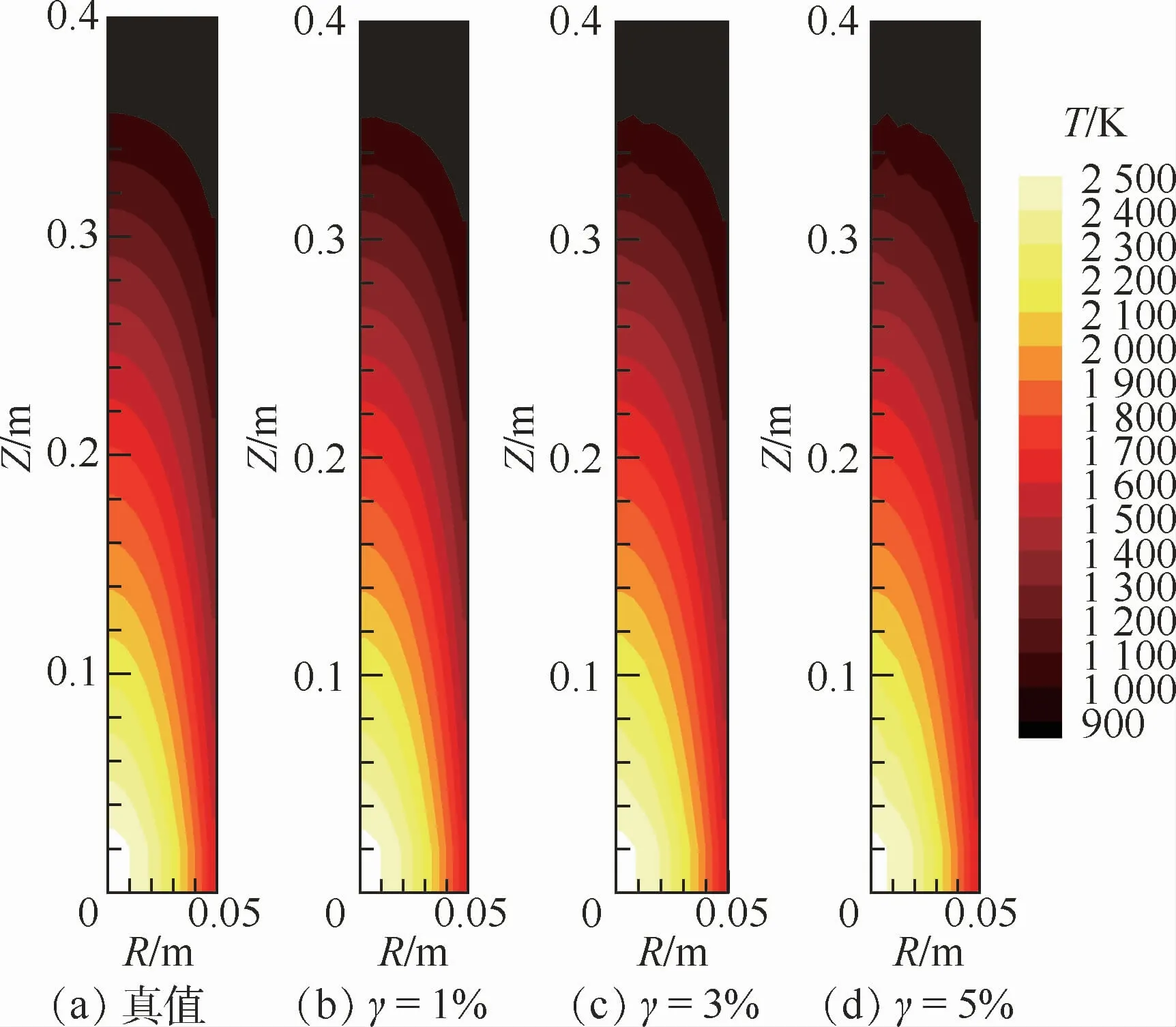
图5 Landweber算法三维温度场重建结果Fig.5 Reconstructed 3D temperature field distribution using Landweber algorithm

图6 LSQR算法重建相对误差分布Fig.6 Reconstruction relative error distribution of LSQR algorithm
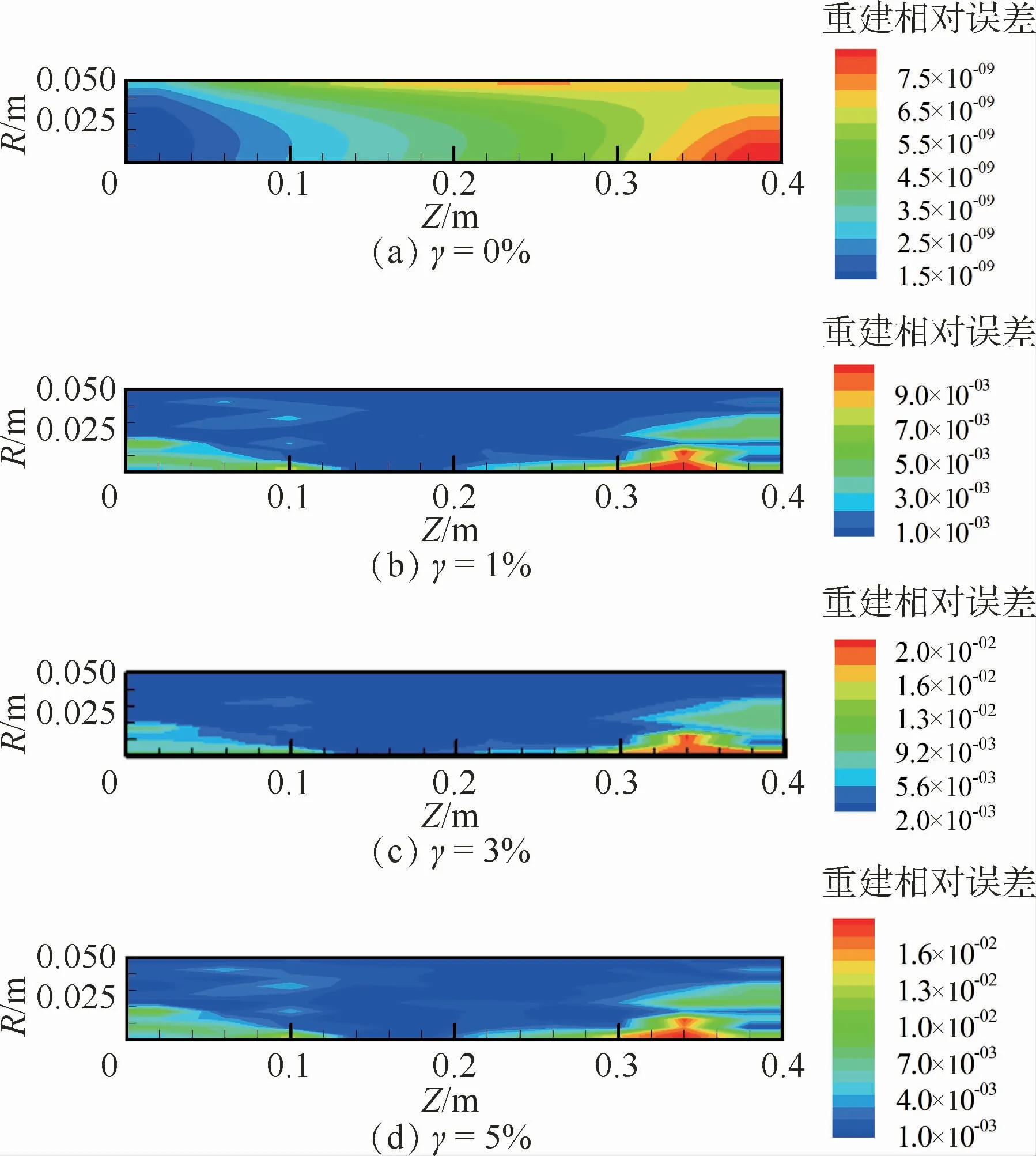
图7 Landweber算法重建相对误差分布Fig.7 Reconstruction relative error distribution of Landweber algorithm
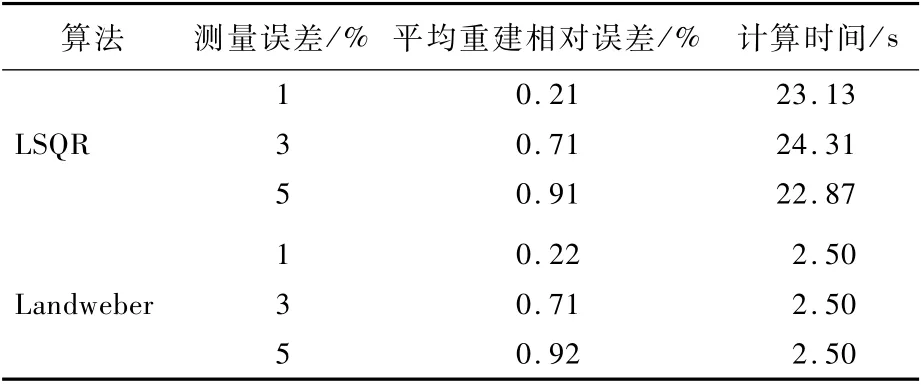
表1 LSQR算法与Landweber算法计算结果对比Tab le 1 Com parison of calcu lation resu lts between LSQR algorithm and Landweber algorithm
进一步从定量的角度分析重建结果的优劣。从重建相对误差中可以看出,无论有无测量误差,利用2种算法都可以得到比较合理的温度场重建结果。在没有测量误差时,2种算法温度场的重建结果精度很高,平均重建相对误差均在10-9量级;随着测量误差的增大,重建相对误差也随之增大;但即使在添加5%的测量误差的条件下,其温度场重建相对误差平均值也分别只有0.91%和0.92%。因此可以看出,2种算法都具有很高的计算精度,且计算结果精度相当。
从图6和图7中可以看出,火焰温度场重建相对误差较大的区域主要发生在火焰径向中心处的轴向两端位置,尤其是顶端区域误差很明显。对于温度场轴对称分布的火焰,由于内部强度的沿程衰减作用,其中心位置的网格单元的自身辐射信号到达相机过程中衰减得最严重,从而导致信息的缺失;并且由于探测线的分布导致穿过轴向两端位置的单元的探测线数量少,从而测量数据中携带轴向两端位置单元的信息相对较少。此外,结合图4和图5所示的温度场真值及图3所示的光场图像可以看出,顶端位置处的介质单元温度较低,其本身测量信号强度较弱,在添加了测量噪声之后,测量信号更容易受到噪声的干扰而失真,因此在这些位置的介质单元的温度场重建相对误差较大。
计算效率是衡量算法优劣的另一个重要指标。本文比较了2种算法在重建温度场时所消耗的时间,如表1所示。可以看出,基于Landweber算法重建温度场所需时间均短于LSQR算法所需时间。当2种算法达到相同的计算精度时,利用LSQR算法需要24 s左右的计算时间,而利用Landweber算法仅需要2.5 s,计算效率差距明显。这主要是由于改进的迭代格式使得Landweber算法的迭代步数大大减少,从而缩短了计算时间。事实上,对于本算例,在存在测量误差的情况下,Landweber算法仅计算了10步,而LSQR算法计算了5 000步,要远多于Landweber算法。因此,在计算效率方面Landweber算法更胜一筹。综合考虑计算效率与计算精度,Landweber算法更适用于基于光场成像的吸收散射性火焰三维温度场重建问题。
4 结 论
1)本文提出了基于光场成像技术的吸收散射性火焰三维温度场重建算法,构建了光场成像模型,采用广义源项多流法作为正问题计算方法,将Landweber算法引入到火焰三维温度场重建问题中,利用Landweber算法计算广义源项分布进而重建出火焰的三维温度分布。同时引入LSQR算法作为对比,以衡量Landweber算法的性能。
2)在理论模型的基础上开展数值模拟研究,计算结果表明无论有无测量误差,利用2种算法均可以很好地重建出介质的三维温度场。随着测量误差的增大,2种算法的重建相对误差均有增大,但使在添加5%的测量误差的条件下,温度场平均重建相对误差也分别只有0.91%和0.92%,仍在可接受范围内。
3)对比结果表明,2种算法具有相当的计算精度,但Landweber算法的计算效率要明显优于LSQR算法,在相同重建精度条件下,Landweber算法的计算时间为2.5 s,而LSQR算法需要24 s,因而Landweber算法要更适用于火焰三维温度场重建问题。结果表明,提出的基于光场成像与Landweber算法的吸收散射性火焰温度场重建方法是可行的,在辐射成像测温领域具有很广阔的应用前景。

