非线性多目标概率约束规划免疫优化算法

张仁崇，张著洪

（1.贵州商学院 计算机与信息工程学院，贵阳550014； 2.贵州大学 大数据与信息工程学院，贵阳550025）

工程优化设计中，诸如水资源调度［1］、再制造加工［2］、电 网［3］、养 分 负 荷 消 减［4］等 问 题 均 可通过性能指标是相互冲突且满足概率约束限制的多目标概率约束规划（Multi-Objective Probabilistic Constrained Programming，MOPCP）加以描述。当随机变量的概率分布信息已知时，可将此类问题转化为等价的确定性多目标约束规划问题，进而可利用数学规划方法或静态多目标智能优化算法求解［5］。可是，在应用中，由于随机变量或噪声的分布常是未知的，导致模型的等价转换变得不可能。一旦赋予随机变量较大的样本容量，可经由静态多目标智能优化算法求解问题的解，但计算开销大，执行效率低。当随机变量的概率分布已知时，如正态分布或指数分布，机会约束可通过复杂的转换变为确定性的约束条件［6-10］；与此同时，重要采样［11］、拉丁超立方采样［12］能被用于估计机会约束的概率，但效率低，估计偏差大。蒙特卡罗（Monte Carlo，MC）随机模拟是一种易于实现且不受限于噪声先验信息的期望值估计方法。基于此，静态采样、动态采样［13］、自适应采样［14-17］已作为随机规划中估计目标函数值和处理机会约束的代表性方法。静态采样简单且易于应用，但计算开销大；动态采样使随机变量的样本大小随迭代次数动态变化，但个体的优劣辨析难；自适应采样要求个体的样本大小由其优劣程度决定，优于动态采样。

从智能优化角度，极为罕见有一般类型MOPCP的成果报道，但源于特定领域的MOPCP的研究已取得一定进展；主要研究集中于模型设计和基于权重系数法的智能优化算法［2，18-21］。张国新等［18］针对空降突破点的决策或供应商的选择问题［19］，构建MOPCP模型，并借助权重系数法转化此模型为单目标决策模型，进而借助随机模拟或双重随机模拟、神经网络获得混合单目标遗传算法。另外，文献［2，20-23］借助隶属度函数设计工程问题的多目标模糊机会约束规划模型，并利用权重系数法或模糊模拟将模型转化为单目标规划模型，进而设计改进型遗传算法或蝙蝠优化算法进行求解。对于MOPCP的多目标智能优化研究，Virivinti和Mitra［24］针对含非线性相关不确定参数的工业磨削加工问题，提出一种基于非支配排序遗传算法（NSGA-Ⅱ）的多目标模糊机会约束规划方法；谢仕炜等［3］针对电网最优负荷削减问题设计多目标多级机会约束规划模型，进而利用拉丁超立方采样处理性能指标和约束条件，并利用NSGA-Ⅱ进行求解。Mehlawat和Gupta［25］基于可靠性理论，构建表征COTS产品选择问题的多目标模糊机会约束规划模型，进而利用顺序偏好近似解方法将该模型转化为双目标规划模型，并利用补偿模糊方法求解此模型的有效解。

综上，探讨执行效率高、寻优效果好、噪声抑制能力强、应用潜力大的新型高性能智能优化算法，是求解MOPCP的关键，但研究成果极为匮乏。免疫优化作为人工免疫系统中极为重要的研究分支［26］，因其具有较好的群体多样性且模块设计灵活，使得与几种经典智能算法相比，在解决多模态优化问题中具有独特的优势，且已获得一系列求解静态或动态多目标优化问题的研究成果［27-29］，但很少触及多目标概率约束优化问题。至于免疫理论是否有助于解决MOPCP仍需深入探讨。危险理论作为不同于自我和非自我识别的免疫理论，解释了免疫应答如何被触发的过程。虽然可借鉴其设计算法解决异常检测、碰撞回避和动态规划问题［30-32］，且求解不确定多目标期望值规划已呈现一定优势［14，33-34］，但是否有助于解决多目标概率约束优化问题仍是悬而未决的。基于此，本文针对随机变量的概率分布未知的一般MOPCP问题，依据危险理论蕴涵的免疫应答机理，探讨多目标免疫优化算法（Multi-Objective Immune Optim ization A lgorithm，MOIOA）。

1 问题描述与概率估计

1.1 问题描述

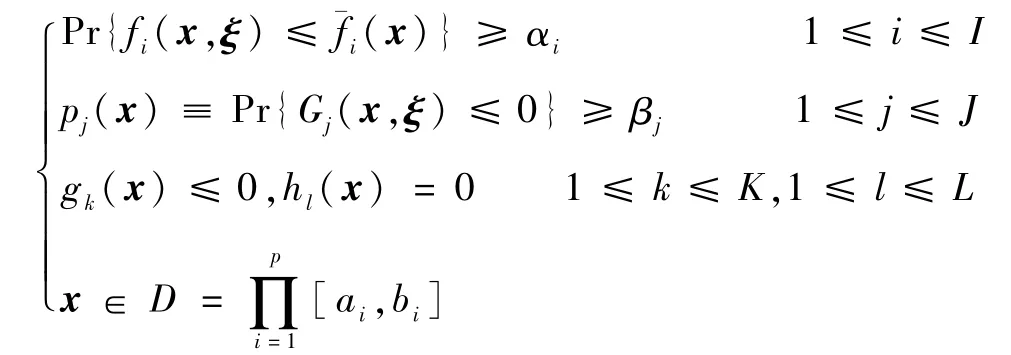
式中：x为决策向量；D∈Rp为有界闭区域；ai和bi为解向量的分量区间的左右端点；ξ∈Rq为分布信息未知的随机向量；Pr｛·｝为概率算子；αi∈［0，1］和βj∈［0，1］为置信水平；fi（x，ξ）和Gj（x，ξ）分别为关于x非线性且连续的随机目标和约束函数；gk（x）和hl（x）为确定性约束函数；I、J、K和L分别为目标向量维数、概率约束个数、不等式约束个数和等式约束个数。在候选解x处，当ξ的样本大小n（x）（简称x的样本大小）给定后，借助MC随机模拟可确定子目标函数的估计值［35］。满足以上所有约束条件的候选解x∈D被称为可信解。引入如下约束违背量函数Γ（x）：

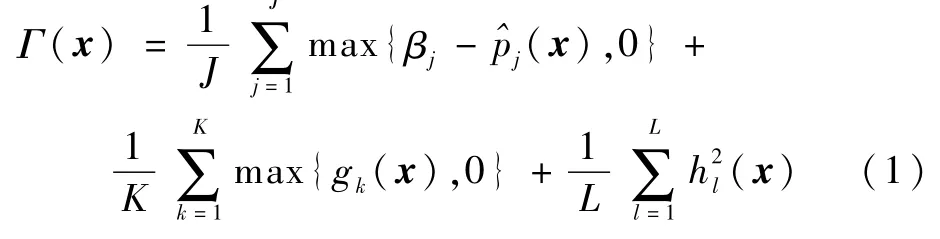
式中：

其中：I｛·｝为指示函数，其若条件为真，则取1，否则取0。显然，当n（x）较大时，由大数定律可获x的经验目标值和概率估计值＾pj（x）。此时，若Γ（x）＝0，则称x为经验可信解，否则称为经验非可信解。借助文献［34］，引入适用于经验可信解之间比较的支配概念以及Pareto最优解的概念。

定义1 对于任意经验可信解x，y∈D，称x支配y（即x≺y），如果：

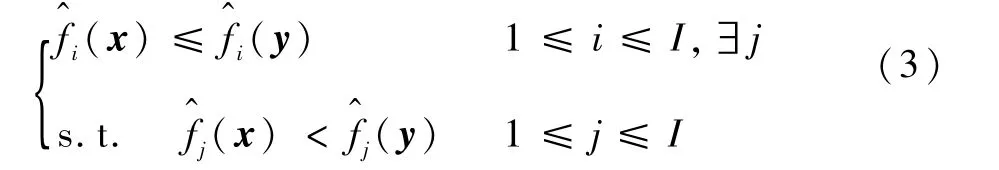
定义2 给定经验可信解x*∈D，若在D中不存在经验可信解x使得x≺x*，则称x*是MOPCP的经验Pareto最优解。

1.2 概率估计

机会约束概率估计法是借助候选解x的样本下限M、样本上限Tn及绝对误差幅度［15］自适应确定随机变量的样本大小，进而估计约束条件中概率函数的值。算法描述如下：

算法1 机会约束概率估计法。

步骤1 输入参数：候选解x∈D，样本大小Tn、M、m，置信水平βj，参数J、δ。

步骤2 置j←1。

步骤3 置s←M（m＋1），依据样本大小s，经由式（2）计算第j个机会约束函数的概率估计值＾pj（x）。

步骤4 计算pj（x）与＾pj（x）的绝对误差幅度：

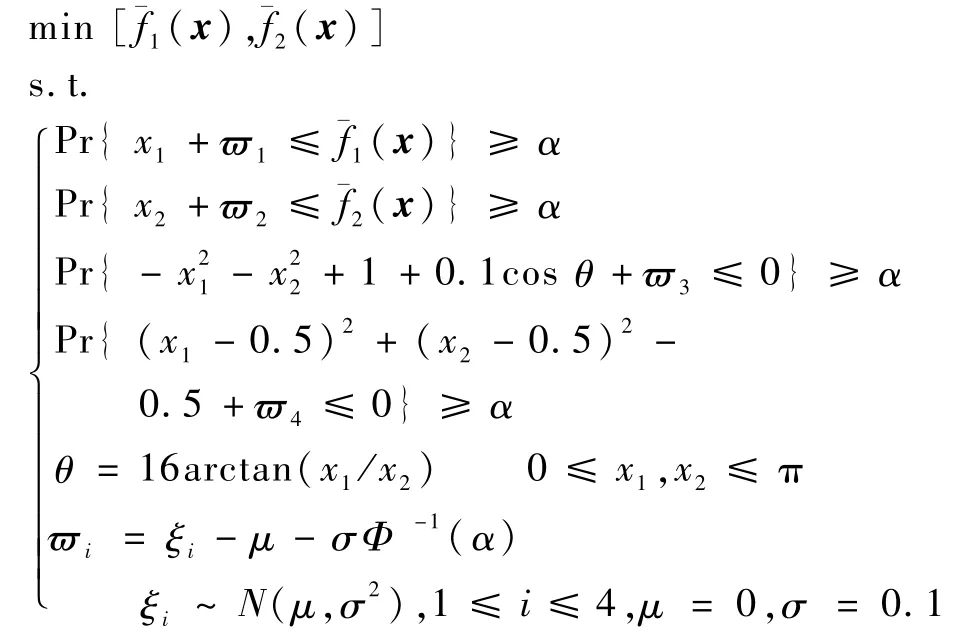
式中：ϖ1、ϖ2、ϖ3、ϖ4、ξi为随机变量；x1、x2为决策向量x的分量；N（μ，σ2）为正态分布；Φ-1（α）为正态分布函数的反函数；μ、σ和α分别为均值、标准差和置信水平。

问题1经由TNK［47］扩展获之。TNK的目标函数的取值范围小，约束函数是非线性的，非支配面是分段连续的。取α＝0.9。在3.1节的评价指标下，各算法获得的统计结果如表1所示，表中：IAE、FR和AR分别为平均约束违背量、可信解所占比例的均值和平均执行时间。各执行一次获得的非支配面和箱线图如图2所示，其中，图2（a）～2（d）为理论非支配面PFtrue和2个算法获得的非支配面，图2（e）～2（f）为CD和CS值的箱线图。

经由表1的IAE、FR可知，以上8种算法均可找到可信解且平均约束违背量较小，其中MOIOA的平均约束违背量最小，获得可信解的概率最高（80.21%）。这些算法均能处理以上问题的约束条件，但MOIOA的约束处理能力最强，原因在于：①MOIOA利用自适应采样策略处理约束条件，这不仅能提高的搜索效率，而且能使优质个体获得的样本大小较大，差的个体获得的样本大小较小；②参与比较的算法均采用静态采样方法处理优化问题的随机因素，同时一个较大的样本大小（300）能使个体的评价值接近理论值。由CD、CS的均值可知，各算法的覆盖密度、覆盖范围的均值之间的差值较小，说明以上算法获得的解分布的差异性较小。由表1中CR均值可知，以上算法获得的解质量视乎没有明显差异，但由平均约束违背量指标IAE可知，MOIOA具有一定的优势。进一步，由图2（f）可知，NNIA、NSGA-Ⅱ、SPEA-Ⅱ的CS箱线图出现异常值，且异常值较小，因此它们获取的部分解属于局部最优解。

此外，经由AR的均值可知，MOIOA的执行效率具有明显优势，且至少是MOEA／DD、MOPSO、NSGA-Ⅱ、SPEA-Ⅱ的6倍，NNIA 的8倍，CMIGA的8倍，以及是AgMOPSO的15倍。

问题2 BNH问题。

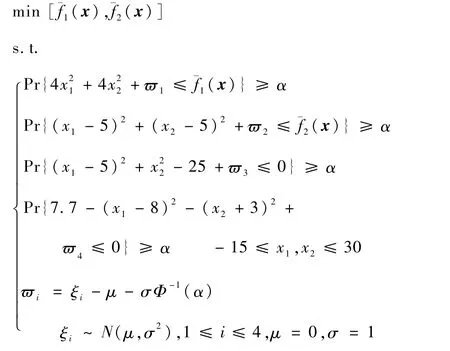
此问题是经扩展BNH问题［47］而获之，其可信解存在的区域是非凸的，部分Pareto最优解位于此区域的边界上。加之，随机变量影响概率约束函数的概率估计和优质解的辨析，求解难度较大。取置信水平α＝0.9。依据以上评价准则，各算法获得的统计结果和平均运行时间如表2所示，箱线图和一次运行得到的非支配面如图3所示。

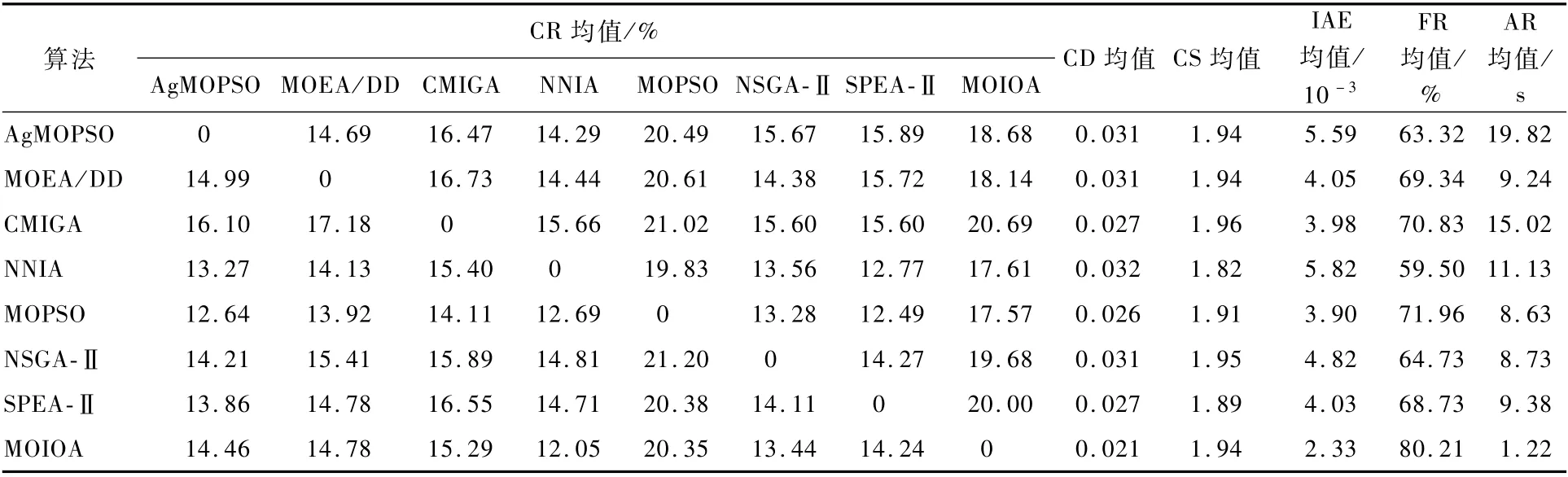
表1 不同算法在α＝0.9下求解问题1获得的统计结果比较Table 1 Com parison of statistical results of d ifferen t algorithm s for Problem 1 w ithα ＝0.9

图2 问题1的非支配面比较与CD、CS值的箱线图比较Fig.2 Comparison of Pareto fronts and comparison of box plots on CD and CS for Problem 1

经由表2的IAE、FR均值可知，MOIOA和参与比较的算法均能高概率地找到可信解，且平均约束违背量均小，此表明以上算法都能处理该问题的约束条件。由CR的均值可知，AgMOPSO的平均覆盖率最高，NNIA和MOIOA次之，而SPEA-Ⅱ获得的解最差。由CD、CS的均值及图3（e）～3（f）可知，AgMOPSO、CMIGA、NNIA、NSGA-Ⅱ、MOIOA获得的解分布较好且覆盖范围较宽，SPEA-Ⅱ次之。由图3（a）～3（d）可知，各算法均能稳定地获得近似最优解。总之，所有算法均能以较高概率发现可信解，但它们的性能有明显差异。综合解质量、解分布和算法产生的约束违背量，MOIOA具有一定的优势，而SPEA-Ⅱ求解以上问题的能力较弱。

此外，经由AR的均值可知，MOIOA的执行效率有明显优势且至少是参与比较的算法的

5倍；MOEA／DD、MOPSO、NSGA-Ⅱ和SPEA-Ⅱ的效率相近且略高于NNIA和CMIGA的效率；Ag-MOPSO的求解所需时间最长。

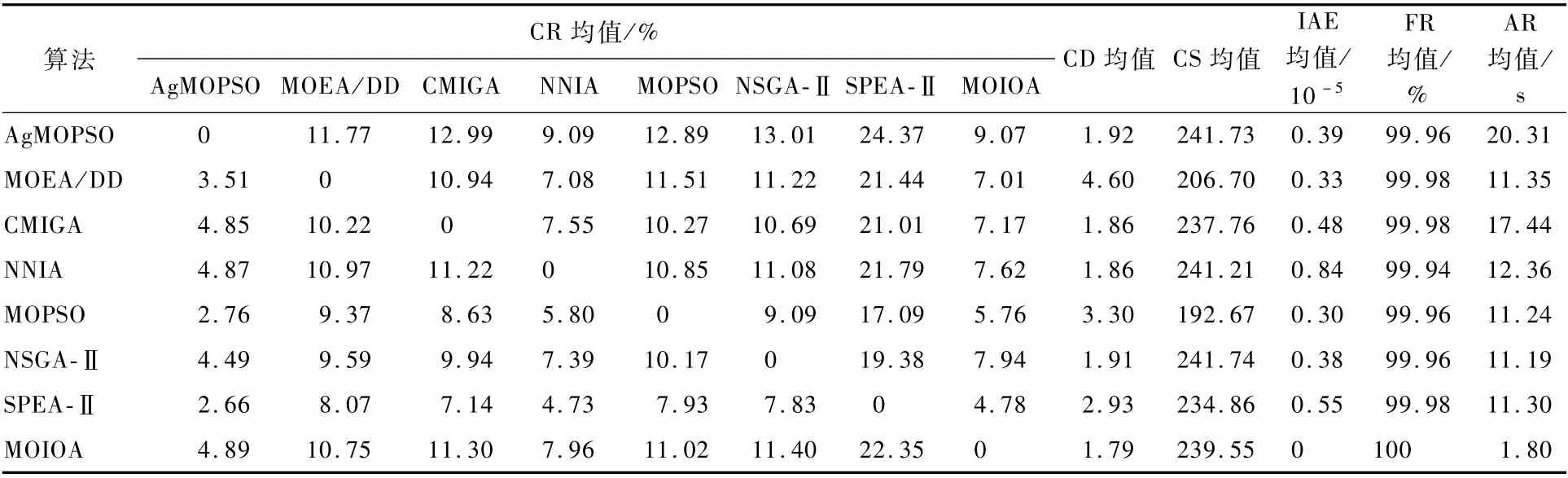
表2 不同算法在α＝0.9下求解问题2获得的统计结果比较Table 2 Com parison of statistical results of different algorithm s for Problem 2 w ithα＝0.9

图3 问题2的非支配面比较与CD、CS值的箱线图比较Fig.3 Comparison of Pareto fronts and comparison of box p lots on CD and CS for Problem 2

3.2.2 工程应用

问题3 盘式制动器设计问题。

该问题经扩展盘式制动器设计问题［48］而获之，其包含4个决策变量（内径、外径、啮合作用力、摩擦表面的个数），5个机会约束函数，目标函数是制动时间、盘式制动器的质量函数。由于此问题的目标函数、约束函数均是高度非线性的，各决策变量的取值范围较大，因此在噪声环境下求解的难度极大。取置信水平α＝0.6。各算法获得的统计结果和平均运行时间如表3所示，得到的箱线图和1次运行生成的非支配面如下图4所示，图4（a）～4（d）为MOIOA和比较算法获得的非支配面，图4（e）～4（f）为CD和CS值的箱线图。

经由表3的IAE、FR均值可知，各算法均能高概率找到可信解，其中CMIGA和MOIOA的平均约束违背量较小。由CR的均值可知，CMIGA平均覆盖率高，MOIOA 和MOEA／DD 次之。经由CD、CS和图4，以上算法获得的解的覆盖宽度与分布没有明显差异；相对而言，CMIGA的解分布相对较差且出现部分解明显偏离Pareto面。由AR均值获知，MOIOA 的搜索效率最高，其是MOEA／DD、MOPSO、NSGA-Ⅱ、SPEA-Ⅱ的3.7倍以上；NNIA的运行速度较慢，但快于CMIGA；Ag-MOPSO的搜索效率最低。

问题4 焊接梁设计问题。

式中：焊缝长度l、焊缝厚度h、梁的宽度t、梁的厚度b为决策变量；Pc（x）为梁的容许屈曲荷载，其表达式为

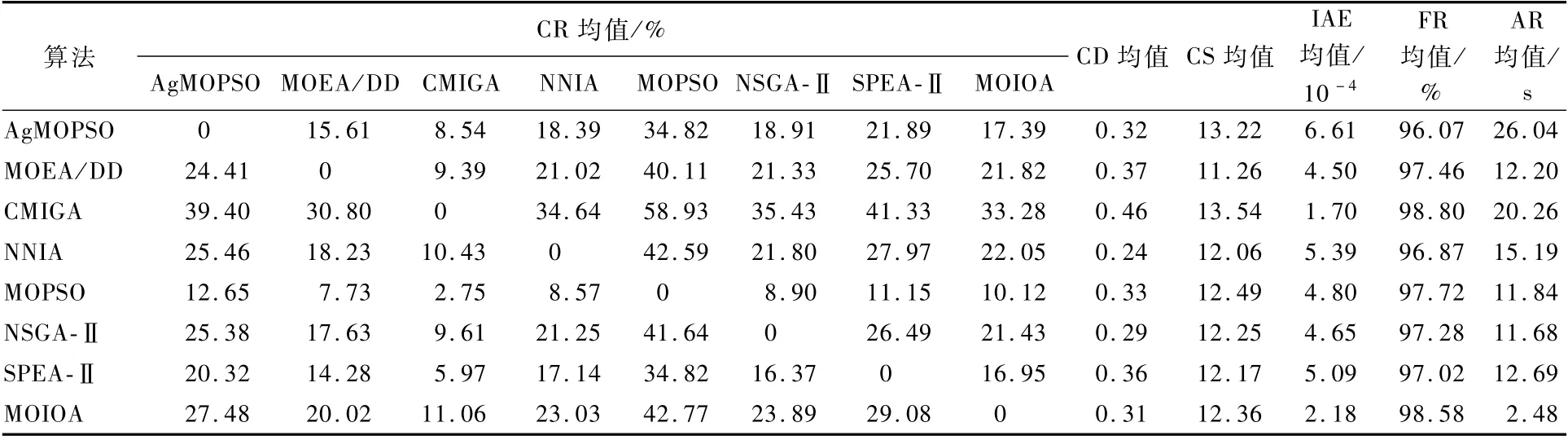
表3 不同算法在α＝0.6下求解问题3获得的统计结果比较Tab le 3 Com parison of statistical resu lts of different algorithm s for Prob lem 3 w ithα＝0.6

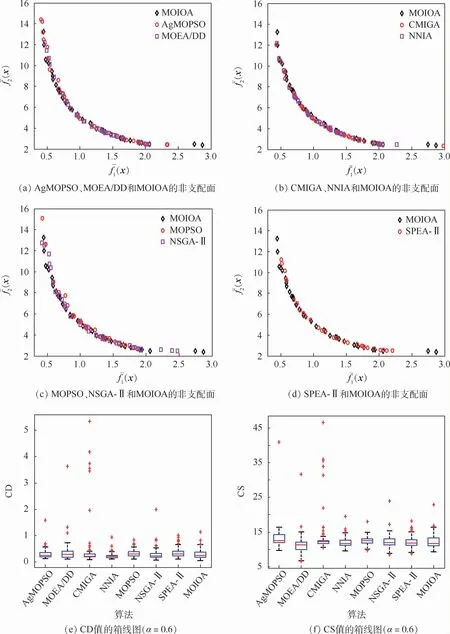
图4 问题3的非支配面与CD、CS值的箱线图比较Fig.4 Comparison of Pareto fronts and comparison of box plots on CD and CS for Problem 3

此问题经扩展焊接梁设计问题［48］而获之，其包含4个设计变量和4个非线性概率约束函数，且以建造费用、端梁的扰度为目标函数；加之第2个目标函数的取值较小，对噪声极其敏感，因此求解该问题较难。取置信水平α＝0.9。各算法获得的统计结果和平均运行时间如表4所示，算法获得的CD、CS值箱线图和一次运行产生的非支配面如图5所示。

经由表4的IAE和FR值可知，以上算法均能以高概率获得可信解；AgMOPSO获得可信解的能力相对较弱。由CR均值得知，MOIOA的平均覆盖率远高于其他算法的平均覆盖率，CMIGA次之。经CD、CS的均值及图5可知，各算法获得的解的分布相似；MOIOA的解分布较宽。因此，MOIOA获得的解分布较好、覆盖范围较宽且解的质量较好。由AR可知，MOIOA具有较高的运算效率，且至少是参与比较的算法的5倍，MOEA／DD、MOPSO、NSGA-Ⅱ、SPEA-Ⅱ次之，AgMOPSO的效率最低。

3.2.3 灵敏度分析

选取TNK测试问题检测MOIOA的搜索性能受参数设置的影响程度。该算法的主要参数包括N、M、λ、pc、ηm及δ。给定α＝0.1；N、M、λ、pc、ηm

及δ的取值的13种不同组合如折线图6（a）所示。MOIOA 在此每种参数设置下，独立运行100次，获得的统计结果如折线图6（b）～6（c）所示。图6（b）中CM 表示算法获得的解的目标值与Pareto面的距离的均值。

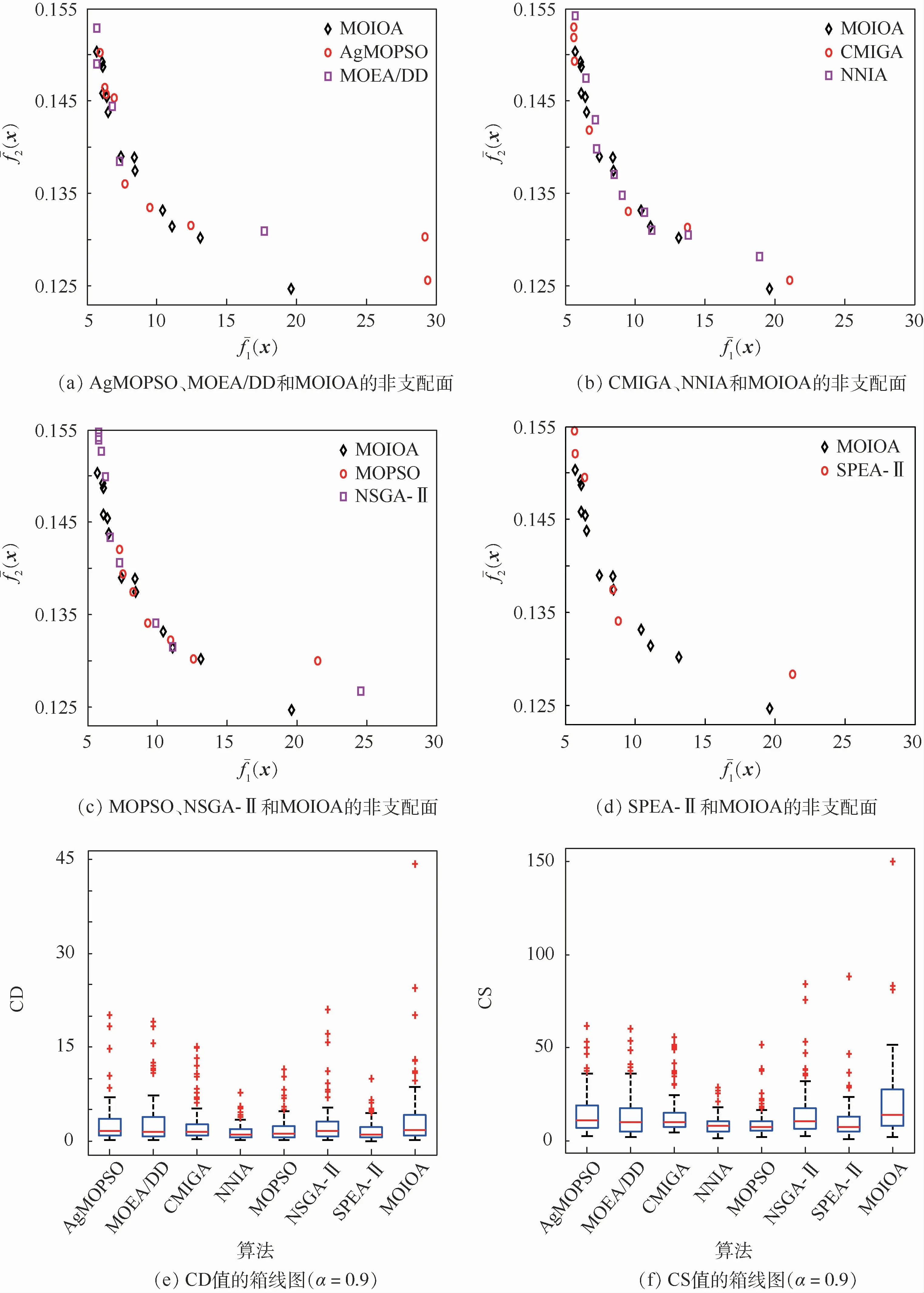
图5 问题4的非支配面与CD、CS值的箱线图比较Fig.5 Comparison of Pareto fronts and comparison of box p lots on CD and CS for Problem 4

由图6可知，MOIOA的解质量对参数设置的敏感度不高。当群体规模N、样本大小M 增大时，CM的均值略小，但运行效率有所下降。算法平均执行时间AR均值随λ、pc的增大而减小，CD、IAE均值随δ增大而减小。因此，尽管参数的设置发生变化，MOIOA也能得到满意的搜索效果，且得到的解的质量差异较小。但是，群体规模、样本大小的设置影响算法的运行效率；参数δ的取值影响算法搜索可信解的性能。

图6 MOIOA的不同参数设置及统计结果比较Fig.6 Different parameter settings of MOIOA and comparison of statistical results

4 结 论

1）多目标概率约束规划是一类具有广泛工程应用背景且也是具有挑战性的随机规划问题。基于此，从免疫学界极为关注的危险理论所蕴含的应答机理出发，设计适用于该类问题的MOIOA。

2）MOIOA中，机会约束概率估计法和目标值估计法通过自适应获取样本大小，分别被用来检测候选解是否为经验可信解以及估计经验可信解的目标值；基于危险理论，设计算法的进化框架，并借助SBX、多项式变异、均匀变异产生多样且高质量的解。

3）计算复杂度分析表明，算法进化初期，个体采样规模小，搜索速度快，此有助于快速获取可信解所在的区域；算法进化后期，通过使采样大小逐渐增大，提高算法的噪声抑制能力，进而有助于获取Pareto最优解。

4）多种具有竞争性的算法参与比较的数值实验表明，尽管MOIOA求解多目标概率约束规划问题在寻优效果方面约占一定的优势，但搜索效率方面有明显优势。