单频RTK动态精度检测法及实验验证
孙艺轩,蔚保国,杨东凯,*,杜毅,汉牟田
(1.北京航空航天大学 电子信息工程学院,北京100083; 2.卫星导航系统与装备技术国家重点实验室,石家庄050000)
随着全球导航卫星系统(Global Navigation Satellite System,GNSS)的发展,单频RTK(Real-Time Kinematic)技术在高精度测绘、精密农业、变形监测、无人驾驶等领域逐渐得到广泛应用[1-2]。单频RTK采用载波相位差分技术,静态定位可以达到厘米级的精度[3]。而对于动态定位精度的量化判定,大多采用高精度仪器组合验证低精度模块的方法,或借助辅助设施,或与网络RTK结果进行比较。例如,文献[4]利用战术级GNSS+INS组合导航系统POS310,将GNSS RTK/INS双频紧组合结果与其中单频数据解算结果进行对比求解精度,得到常规固定解三维精度约5 cm。文献[5]采用Piksi定位模块,借助铁轨与旋转支架进行实验求解RTK精度,判定三维动态精度约3~5 cm。文献[6]利用实验场地附近IGS站数据后处理解算的位置为标准,判定单频RTK平面定位精度在3 cm 以内,高程定位精度低于10 cm。上述做法一般需要的仪器设备较多,覆盖范围较局限。针对上述问题,本文提出一种无需额外辅助设备、适用地域较广的单频RTK动态精度检测法。该方法仅利用2台GNSS接收机构成RTK系统,无需惯性导航设备等进行辅助测量。动态定位精度的评定借助实验流程中部分静态数据的计算结果,因此不必在CORS站、IGS站附近场地进行测试。实验证明,本文方法具有较高的可靠性,可以准确量化单频RTK动态厘米级的定位精度。
1 单频RTK定位模型
基于高精度载波相位观测量,单频RTK技术是一种实时动态高精度定位技术[7]。常用双差观测模型,其卫星轨道、钟差等残余误差可以忽略不计[8]。对于短距离用户,可以不考虑电离层、对流层等大气残差[9]。RTK 单频双差观测原理如图1所示。
流动站u和基准站r同时追踪卫星i和卫星j,定义这2个站在同一时刻对卫星i、卫星j的单差载波相位测量值为,由它们所组成的双差载波相位测量值定义为

图1 RTK单频双差观测原理示意图Fig.1 Schematic diagram of RTK single-frequency double-difference observation principle

双差载波相位观测方程与双差伪距观测方程分别为[10]
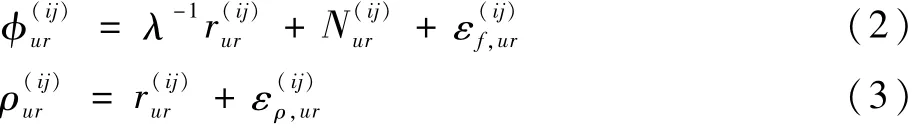
在地心地固坐标系(ECEF)中,接收机的位置坐标及状态参数表示为[4]

式中:rr为接收机三维坐标向量;Nur为北斗/GPS对应的双差整周模糊度。

由上述公式计算Kalman滤波的初始状态向量x0和观测向量y。采用Kalman滤波方法,计算滤波浮点解。在状态向量更新后进行双差整周模糊度固定,从而获取更高精度的固定解,加快收敛时间[11]。本文采用LAMBDA方法进行模糊度的固定[12],用ratio值衡量模糊度固定可靠性,判断求得的整数解是否满足要求。
2 单频RTK动态精度检测法
为了准确得到量化的动态RTK精度,本文设计了一种单频RTK动态精度检测法用于实际测试,进一步提出了相应的定位精度的计算方法与可靠性检验方法。
2.1 建立基准直线
本文方法首先需要在地面建立基准直线,作为具有一定高度的RTK终端的底部运动轨迹的基准值。为了保证实验数据充足,便于后续对方法的可靠性检验,往往需要在地面建立多条平行的基准直线。在每条基准直线上选取至少4个参考点进行静态测试,取每个参考点的静态数据的平均值作为该点的参考值,再利用整体最小二乘法[13]将上述参考值拟合,得到该基准直线L的三维表达式。整体最小二乘法将空间直线方程所需的6个参数简化为4个,将空间直线拟合问题转化为整体最小二乘的参数求解问题,最终得到三维表达式为
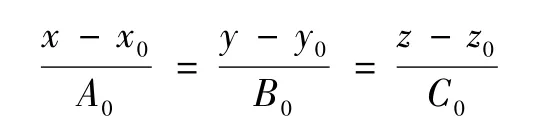
式中:该基准直线经过点(x0,y0,z0),其方向向量为n0=[A0,B0,C0]。
2.2 测量组合数据
在基准直线上等间隔选取q个静态点,令具有一定高度的RTK终端沿基准直线按如下运动方式采集数据:将首尾2个静态点分别作为运动的起点与终点,在起点进行t时长的静态测试,再匀速运动至下一个静态点进行t时长的静态测试,重复上述运动直至终点。定义上述过程得到的静态数据与动态数据集合为组合数据。处理时分离静态数据与动态数据,可以求得动态过程的平均速度。
2.3 精度计算
对组合数据中的静态数据进行上述整体最小二乘拟合,得到检核直线l的三维表达式,作为具有一定高度的RTK终端运动轨迹的基准值;再与组合数据中的动态数据一起代入式(8),计算动态点到检核直线的距离di。


2.4 可靠性检验
为了验证数据的准确性,进一步判断实验可靠性,针对多条平行的直线运动轨迹,可以通过计算间距误差τ进行可靠性检验。此时,以基准直线为参考,以检核直线为检测对象。设基准直线间距为Qi,与其对应的检核直线间距为qi,以2种间距之差绝对值的平均值作为间距误差τ,即

式中:n为间距数量。若该可靠性指标的数量级低于动态定位精度的数量级,认为组合数据准确,由此计算得到的精度可信,本次实验具有较高可靠性;若不符合条件,认为本次实验不可靠,需要重新测量组合数据。
上述单频RTK动态精度检测法的流程如图2所示。

图2 单频RTK动态精度检测法流程Fig.2 Flowchart of single-frequency RTK dynamic accuracy detection method
3 实验验证和分析
3.1 实验系统搭建
本文单频RTK系统由测试系统和数据处理系统组成,系统组成模块如图3所示。
测试系统主要分为两部分:基准站系统与流动站系统,2个系统硬件组成结构一致。基准站系统与流动站系统均由高精度天线、GNSS单频接收板卡及无线通信模块组成。本文采用深圳华大北斗科技有限公司HD9100系列的GNSS单频板卡[14],该板卡支持北斗B1频点和GPS L1频点,支持RTCM3.2格式数据传输,实验采样率为1Hz。
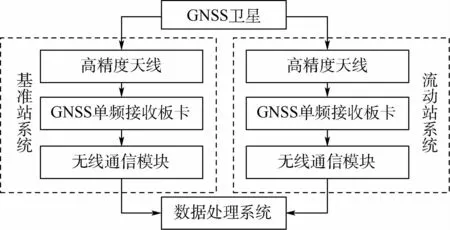
图3 系统组成模块Fig.3 Block diagram of system composition
数据处理系统由连接2个无线通信模块的计算机与处理软件组成。电脑通过无线通信模块接收来自测站的原始观测数据,并通过不同频点区分基准站和流动站的数据。利用单频RTK定位软件进行位置求解并输出结果,得到测量点的坐标。
3.2 实验与结果分析
本文利用北京航空航天大学操场跑道的白色直线设计实验,分析单频RTK精度。单频RTK动态精度检测法先建立基准直线,再测量组合数据,最后进行精度求解与可靠性判断。
3.2.1 基准直线的建立
1)实验内容
在北京航空航天大学操场取16m长的直线跑道作为基准直线,在其上等间隔选取包括轨迹起点与终点的5个地面参考点。本次实验共测量4条16m直线跑道,共计20个地面参考点。在每个参考点处进行约为90 s的静态RTK测量,将每个点处测量值的均值作为其真实坐标。
2)精度分析
在观测时段内,静态定位结果的位置偏差在一定意义上可以反映出定位结果的优劣[15]。由于三维静态误差分布未知,适宜用RMS衡量观测值与真实值之间的偏差[16],计算公式为

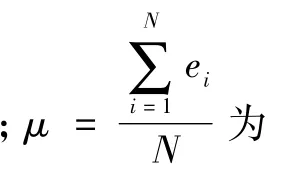
表1列出了20个地面参考点E(东)、N(北)、U(天)3个方向上RMS的最大值与最小值。可见,高程(U)误差相对较大,RMS最大为1.9 cm,平面上东(E)、北(N)方向较小,RMS最大不足1 cm。定位精度较高,满足实验要求,可以用于拟合基准直线L1、L2、L3、L4。

表1 东北天方向的RMS最值Tab le 1 M axim um and m inim um RM S in E-N-U
3.2.2 测量组合数据
1)实验内容
如图4所示,将流动站系统架设在小车上,推动小车沿基准直线运动。先等间隔选取5个静态点,以第一个静态点作为轨迹起点,在起点进行90 s的静态测量,再匀速运动至下一个静态点进行等时长的静态测试,重复上述运动直至终点。实验轨迹如图5所示。
2)精度分析
本文共进行了2次速度不同的实验测量,平均速度分别为0.13m/s和0.35m/s。在每次实验中,根据组合数据中每条直线上的5个静态点数据拟合得到检核直线l,与组合数据中相应的动态数据一起代入式(8)得到动态点到相对应的检核直线l的距离d。每次实验得到4条检核直线l1、l2、l3、l4,2次实验的动态定位坐标误差d的时间序列分别如图6(a)、(b)所示。

图4 实验实拍图Fig.4 Real shot of experiment

图5 实验轨迹图Fig.5 Trace diagram of experiment
2次实验坐标误差d的RMS、最大值dmax和平均值列于表2。可以看出,2次实验速度不同,误差离散程度随速度提升而略微增大,但平均偏离相差不大,均在2 cm左右,最大偏离均不超过5 cm。初步认为单频RTK 系统在直线运动下通过该方法评定的动态定位精度约为2 cm。
图7展示了平均速度为0.35 m/s实验的动态点与检核直线。由于直线拟合得出的是点到直线的最短距离,整体误差偏小,考虑到实际运用中测量点与真实值的对应关系[2],据此判定单频RTK系统的动态误差为2~5 cm。
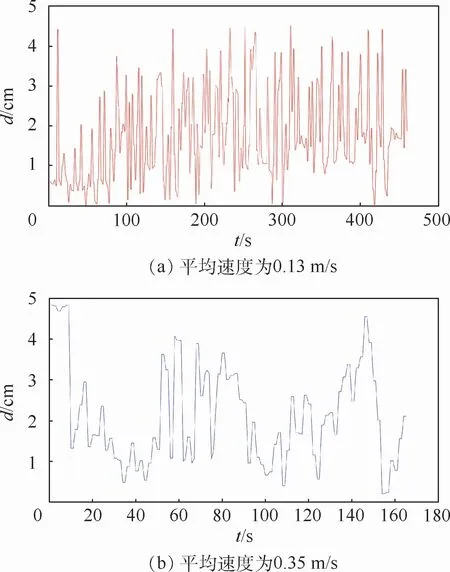
图6 动态定位坐标误差的时间序列Fig.6 Time series of coordinate errors in dynamic positioning
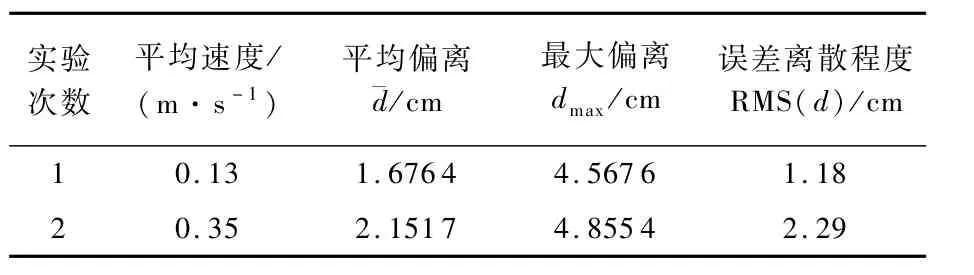
表2 动态实时定位实验精度分析Table 2 Accuracy analysis of dynam ic real-tim e positioning experim ent
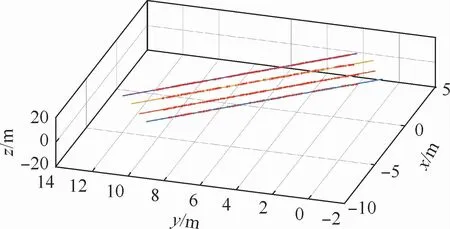
图7 平均速度为0.35 m/s时实验的动态点与检核直线Fig.7 Dynam ic point and checking line of experiment with average speed of 0.35 m/s
3.2.3 可靠性检验
针对平均速度为0.13m/s、0.35m/s的2次实验,分别将基准直线间距Q1,Q2,Q3与检核直线间距q1,q2,q3代入式(9)计算间距误差,得到τ1=0.004m,τ2=0.005m,均在毫米级别,表明本次实验组合数据准确,精度可信,初步表明单频RTK动态精度检测法可用,具有较的好可靠性。
4 结 论
1)针对静态RTK定位,用RMS衡量数据精度,得到东北天(E-N-U)3个方向定位精度。其中高程(U)误差相对较大,约为2 cm,平面上东(E)、北(N)方向较小,约为1 cm。
2)针对单频RTK动态定位精度的量化,基于RTK动态、静态实验组合数据,提出了以动态相对静态的平均偏离的动态精度衡量方法,实验结果表明,在不同平均速度下单频RTK实时动态定位精度约为2~5 cm。
3)提出间距误差τ作为可靠性检验指标,验证单频RTK动态精度检测法的可靠性,证明了空间直线的整体最小二乘法的可适用性。初步表明单频RTK动态精度检测法贴合实际,可以准确地评估实时动态单频RTK精度。
4)本文方法理论上可以用于双频RTK动态精度检测,但有待于进一步实验验证。

