基于散射光强度的碳黑团聚体分形结构和粒径分布同时反演

张俊友，齐宏，*，王一飞，任亚涛，阮立明

（1.哈尔滨工业大学 能源科学与工程学院，哈尔滨150001；2.哈尔滨工业大学 空天热物理工业和信息化部重点实验室，哈尔滨150001）

碳黑是一种由碳氢化合物不完全燃烧产生的含碳物质，纳米级的碳黑初级颗粒会因布朗运动碰撞而互相附着，通常会形成具有分形结构的团聚体，即碳黑团聚体［1］。在航空发动机燃烧室中，碳氢燃料的燃烧也产生碳黑团聚体。高温高压下，碳黑团聚体不但会磨损机体，而且燃烧室内的火焰传热以辐射换热为主，碳黑团聚体的辐射特性会影响燃烧室的辐射换热［2-3］。因此，碳黑团聚体的粒径和辐射特性等性质对于航空发动机燃烧室的寿命和性能有着重要意义。此外，航空发动机的高空排放也是大气中碳黑团聚体的重要来源之一。大气中的碳黑颗粒吸收太阳辐射，加热大气并冷却地表，因此具有碳黑团聚体被认为是工业时代气候变化的第二重要的人类因素［4］。同时，含有有毒物质的碳黑团聚体对人类健康有害，可能导致慢性肺部疾病、肺癌、哮喘等疾病［5］。由此可见，碳黑团聚体对于火焰中辐射换热、气候变化和空气质量都至关重要［6］。因此，碳黑团聚体的性质测量研究吸引了大量海内外学者的关注。

本文提出了一种利用光学信号间接测量碳黑团聚体结构特征和光学特性的方法。将光学方法用于火焰中碳黑团聚体的性质测量研究具有以下特点：高灵敏度，原位测量，不对样本产生干扰等。目前，已有学者开展了利用不同光学信号反演得到火焰中碳黑物理性质的研究工作。其中有代表性成果包括：1992年Sorensen等［7］提出了一种利用光的散射-消光信号实现原位光学测定碳黑团簇的基本粒子直径、每簇的基本粒子数和分形维数的新方法。2007年Iyer等［8］同样采用散射-消光信号来实现光学参数的重建。2011年Link等［9］使用3个角度的散射光信号确定多分散团聚体的参数包括粒子尺寸分布和分形维数。2016年Amin和Roberts［10］使用瑞利-德拜-甘斯多分散分形团聚体（RDG-PFA）散射理论计算2个角度的散射-消光信号，分别反演碳黑的多种物理性质，包括碳黑体积分数、基本粒子直径、团聚体平均回转半径和基本粒子数量密度。2017年Moghaddam等［11］利用多体T矩阵（MSTM）模型的精度和瑞利-德拜-甘斯分形团聚体（RGD-FA）模型的计算速度，实现从散射光的角度分布反演气溶胶中碳黑团聚体的粒径分布和结构特征。但是上述研究存在一个共性问题，就是在精确已知很多物性的前提下进行反演过程，这大大提高了反演测量准备工作的难度，使反演方法偏离真实情况。实际上，很多物性是很难提前获得或者精确测量的，这些已知参数的不确定度会严重影响反演方法的精度，使得提出的方法具有很大的局限性，甚至在实际测量中不具备可行性。本文为了克服这一问题，使用2种不同类型的光学信号，增加反问题输入信息，实现了在关键物性参数都未知和测量误差等诸多干扰下，碳黑团聚体形状特征参数和光学性质参数精确且稳定的同时反演。

1 正问题

1.1 分形团聚体

本文研究对象为碳黑颗粒系统。如图1所示，单个碳黑团聚体由许多个近似球形的基本粒子组成，基本粒子间互相吸附，形成链状的分形结构。如果假设所有基本粒子为球形且具有相同的粒径，就可以使用分形理论对单个碳黑团聚体的几何特征进行参数化描述［12］：

图1 碳黑团聚体分形示意图Fig.1 Schematic of fractalmorphology of soot aggregate

式中：Np为单个碳黑团聚体中基本粒子总数；kf为分形前置因子；Rg为碳黑团聚体的回转半径；dp为碳黑团聚体中基本粒子的直径；Df为分形维数。

测量的目标区域内有大量不同的分形碳黑团聚体。如果以回转半径表征不同碳黑团聚体的尺寸，回转半径的分布函数近似满足对数正态分布［12］：

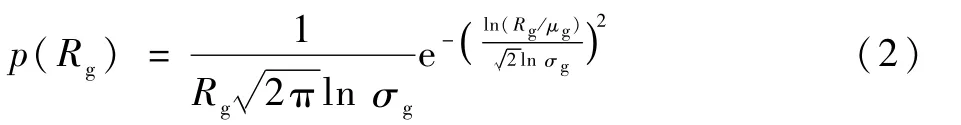
式中：μg和σg为分布函数的特征参数，分别为Rg的平均值和标准差。

1.2 RDG-PFA散射理论

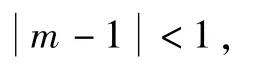
RDG-PFA模型中，基本粒子的微分散射截面为［12］

单个碳黑团聚体的微分散射截面为［12］

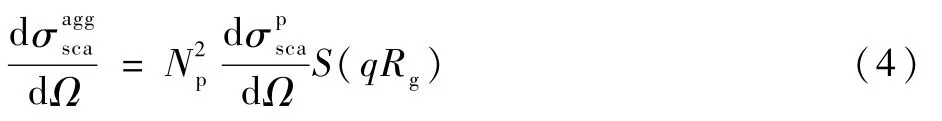
其中：q＝（4π／λ）sin（θ／2）为RDG-PFA散射理论中一个重要的物理量，与散射角θ和入射激光波长λ有关；M＝4；C1＝2M／（3Df）；C2＝C3＝0，C4＝1。

因此，整个测量体积内所有碳黑团聚体的角度散射光强度为［12］

式中：α为测量系统的效率，介于0与1之间；Iinc为入射光强度；nagg为激光探测体积内的碳黑团聚体数量密度，即单位体积内碳黑团聚体的个数。

将式（1）、式（3）和式（4）代入式（6），可以整理成如下形式：

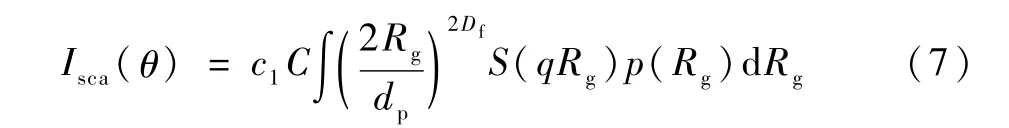
式中：C为一个与复折射率m和碳黑团聚体数量密度nagg有关的函数，C＝naggF（m）；c1为多个常数参数的函数，c1＝f（α，Iinc，dp，k，kf）。

此外，单个碳黑团聚体的吸收截面为［12］

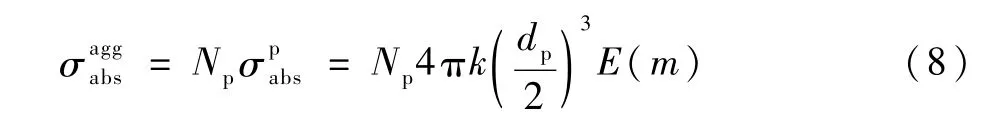
光谱准直透射率为［12］

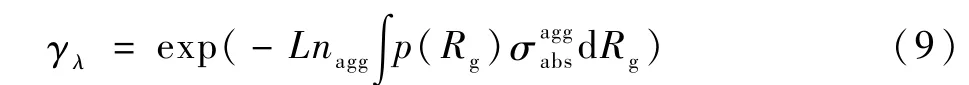
式中：L为激光在测量体积内的行程长度。

将式（1）和式（8）代入式（9），可以整理成如下形式：

式中：c2＝f（r，L，dp，k，kf），r＝F（m）／E（m）。

1.3 实验装置

如图2所示，本文采用了文献［14］中提出的广角光散射（WALS）测量装置，用于在10°～170°的宽角度范围内收集散射光。通过透镜，将散射光成像到ICCD相机检测器的芯片上，并允许以约0.6°的角度分辨率同时采集全散射图像［15］，因此通过散射图像可以得到散射光在不同角度上的强度。获取某一散射角强度的具体实验操作请参考文献［14-15］。反射镜上有2条相对的狭缝，保证激光进出，进出的激光都会被束流拘束器收集，因此可以得到光谱准直透射率。本文提出的反演方法中，在10°～165°范围内每隔5°取一个散射角，共计32个散射角，作为反演信号。

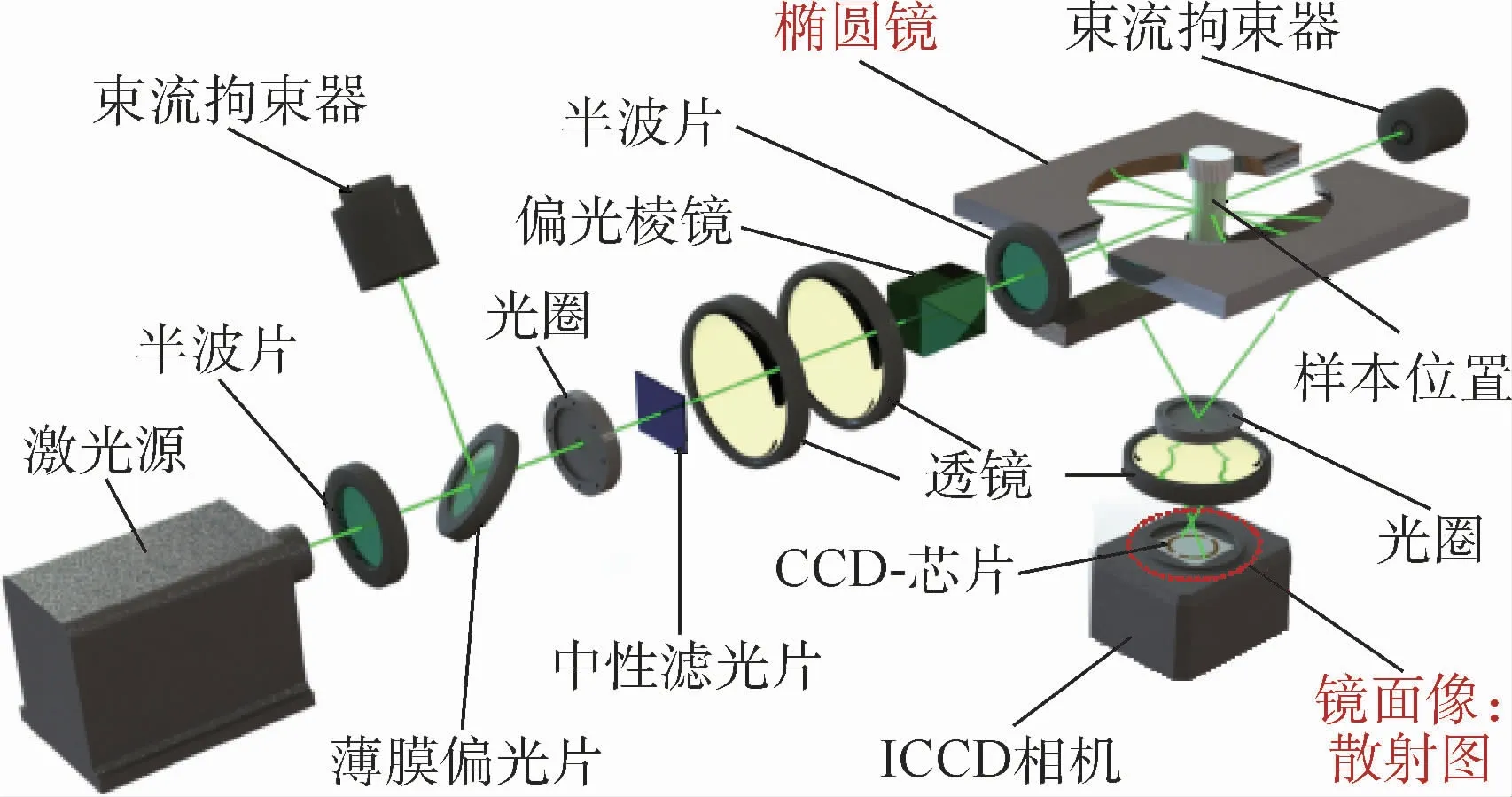
图2 广角光散射测量装置［14］Fig.2 W ide angle light scattering measurement system［14］

2 反问题

反问题的目标是同时反演4个目标参数，分别为C、分形维数Df、粒径分布特征参数μg和σg。如图3所示，整个反演过程如下：

图3 反演过程Fig.3 Inversion procedure

步骤2 目标参数的预测值更新，代入RDGPFA模型计算得到不同散射角度的散射光强度的预测值。）和）代入适应度函数计算适应度值，根据适应度值反演算法更新目标参数的预测值，使测量值）和预测值）逐渐接近。

步骤3 当适应度值Fobj小于目标值eps或者迭代次数T达到最大迭代次数maxgens时，反演过程停止并输出目标参数的最终预测结果。

解决反问题的过程就是使目标函数值最小化的过程。按照步骤2中描述的过程，可以将目标函数定义为

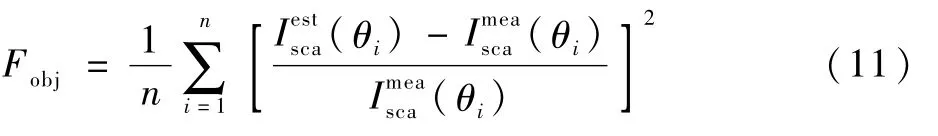
式中：下标i代表第i个散射角的散射光强度，共计n个散射角。

我国高校肩负着为社会建设发展培养人才的历史使命，近年来随着我国社会及经济的腾飞，对于人才的需求在不断增加，高校的地位得到了进一步的提升，因此，必须要有效地做好高校的建设及发展工作。

在最初的反演中，仅仅采用了多角度的散射信号。但随着测量误差的增大，4个目标参数的反演误差无法同时满足精度要求。因此，需要增加更多的光学信号来反映碳黑团聚体的内部信息，仅仅增加散射角数量效果微弱。加入光谱准直透射信号是一个很好的选择，在已有的设备条件下，光谱准直透射率是方便实现的，并且可以实现与散射信号的同时测量。在后面的分析中也证明了采用散射与透射信号结合的方法要比仅使用散射信号病态性更弱，有利于在有误差干扰下反演过程向全局最优解收敛。此时，目标函数变为

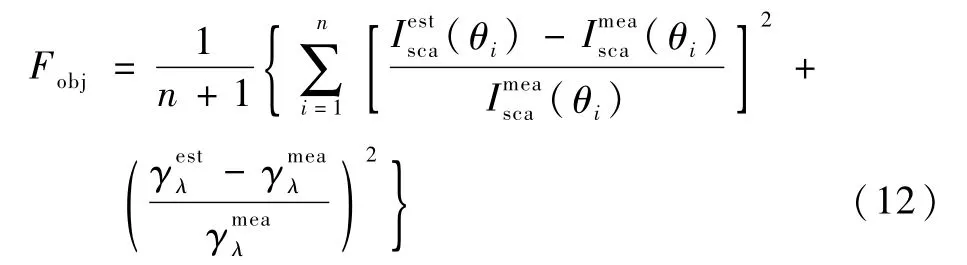
本文使用的CMA-ES算法的具体原理和源代码在文献［16］有详细介绍，不再赘述。

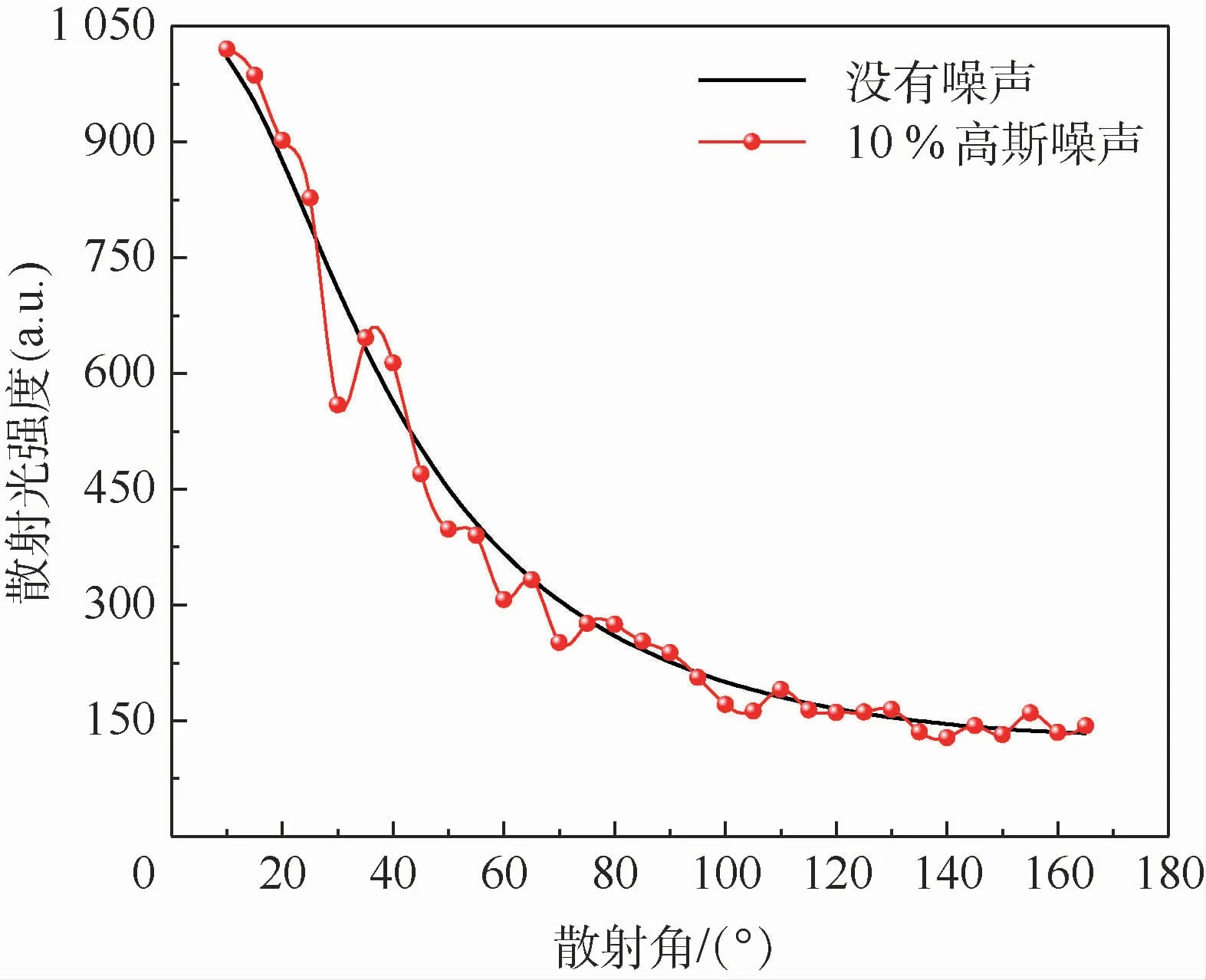
图4 没有噪声与10%高斯噪声下的角度散射光强度对比Fig.4 Comparison of angular light scattering intensity under no noise and 10% Gaussian noise

3 结果和讨论

3.1 残余适应度分析

为了说明本文采用的多角度散射-准直透射率组合信号的优势所在，对比目标参数分布范围下的残余适应度分布情况。由于受限于图片表达的维度，最多只能分析2个参数的残余适应度值的分布情况，为了展现问题的收敛特性，图片中采用3D云图与2D投影结合的展示方式。

图5（a）、（b）分别为复折射率m采用2种信号组合时的残余适应度分布。可以发现，在仅使用散射信号的情况下，复折射率反演结果不唯一，体现在图5（a）中成谷状的收敛区间，这意味着反演存在严重的多峰情况，使反问题精确求解变得非常困难。加入透射信号后，有效改善了这一现状，使适应度函数收敛于一点，不仅使目标参数的精确反演变得易于实现，也会使反演收敛速度明显提高。

图5 两种信号方案下的残余适应度分布Fig.5 Residual fitness distribution contour under two signal schemes

3.2 碳黑团聚体参数的同时反演结果及分析

本文中入射激光的波长是806.5 nm，从文献［17］中查得在此波长下乙炔火焰碳黑的复折射率m＝1.57-0.46i。2个粒径分布函数的特征参数的真值定为μg＝90 nm和σg＝1.6，相应的回转半径范围为0～500 nm。目标参数C根据所含各个参数计算，C＝0.8。分形维数Df根据其数学意义应该为1～3，本文定义Df＝1.65，可以产生合理的分形碳黑团聚体。各个参数在反演时需要给定一个搜索范围，为了证明本文方法在大搜索范围的适用性和稳定性，所选取的搜索范围都尽可能得大，初始值就在此范围内线性随机产生。如表1所示，每个参数的搜索范围都是远远大于可能存在的区域，如μg不可能超出最大500 nm或小于最小0 nm的粒径范围。

实际上，CMA-ES算法除了初始化过程外并不使用此搜索范围，而是向全域范围扩展式地搜索，因此实际的搜索范围要比给定的搜索范围更大。此外CMA-ES算法虽然有许多算法参数，但因为其引入了参数自适应策略，算法参数会在算法进程中自行调整，因此并不需要为寻找合适的算法参数费心。但算法的收敛精度和最大迭代次数需要声明，如表2所示。

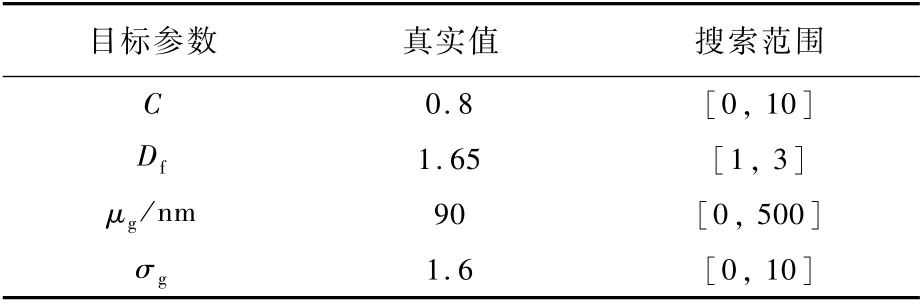
表1 目标参数的真实值和搜索范围Tab le 1 O riginal value and search range of target param eters

eps是目标收敛精度，设eps＝10-10，只有在没有噪声的情况下，反演才会因目标函数值满足目标精度而停止。而有噪声存在时，最终的目标函数值都会降到一个相对最低值。maxgens是最大迭代次数，设为maxgens＝1 000。CMA-ES算法是一种随机算法，具有一定的随机性。因此，每种情况都重复50次以减少随机性的影响。限于篇幅，本文只展示了所有算例中的一个，其余基于不同目标参数值的算例都能取得类似精度的反演结果。

评价反演结果的相对误差绝对值定义如下：

式中：εrel为相对误差；zori为每个参数的真实值；zest为预测值。相对误差的最大可接受值定为1%。本文使用标准差来评价反演结果的集中程度，即数据集的标准差越大数据越分散，分布范围越大，反之，数据集越集中，分布范围越小。

表3列出了在不同高斯噪声下使用不同信号组合的目标参数反演结果。可以发现，在没有噪声的情况下，2种信号方案都可以非常准确地反演4 个参数，每个参数的相对误差都小于0.005%，而且标准差也都达到很小的数量级，说明50次反演结果都很好地收敛到全局最优解（目标参数真值）。随着噪声的增大，4个目标参数的相对误差都不可避免地增加。仅采用散射信号，4个参数在6%和10%的高斯噪声下都超出可接受范围（1%），其中μg更是达到了20%以上，而且标准差的数量级对比没噪声的情况骤增。不过对比6%，在10%下误差及标准差变化趋势不是很明显。

表2 CM A-ES算法的参数设定值Tab le 2 Param eter value setting of CM A-ES algorithm

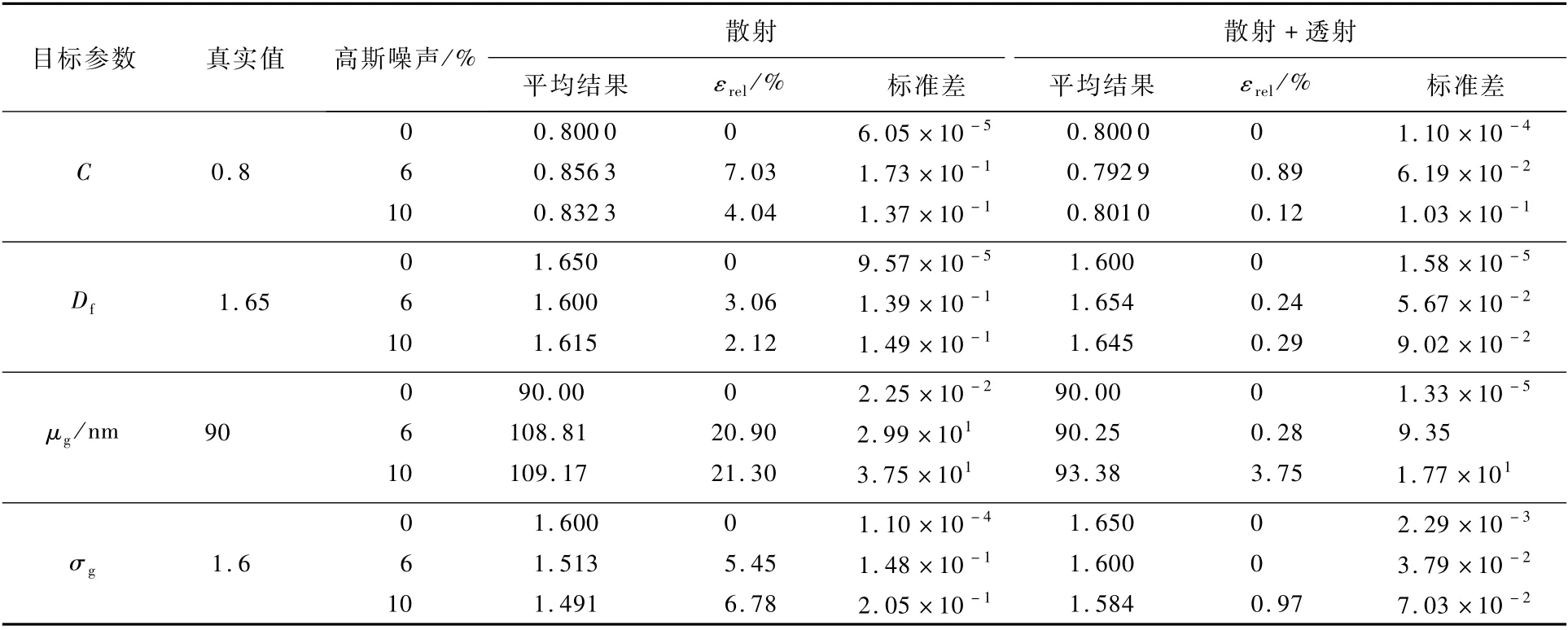
表3 不同高斯噪声下使用不同信号方案的目标参数反演结果Table 3 Inversion results of target param eters ob tained by different signal schem es under differen t Gaussian noise

采用散射＋透射的信号组合，除10%高斯噪声情况下μg的相对误差超出1%外，其余情况下，各个参数的相对误差都小于1%，达到可接受范围。随着噪声增大，反演结果的相对误差和标准差基本上呈增加趋势，不过此信号组合有效限制了增加的幅度。对比相同噪声下仅采用散射信号的反演结果，可以发现同时采用散射和透射信号明显优化了反演结果，成功地将糟糕的反演结果提升到精确反演的程度，尤其是测量误差不超过6%的情况下。各个参数的反演误差和标准差数量级都显著下降。这说明在噪声干扰下，引入透射信号有效改善了问题的病态性，提高了反演的稳定性与抗噪性。

此外还发现不论什么情况下，μg的参数标准差和相对误差都是4个参数中最大的，这与3.1节的残余适应度云图的分析结论相吻合，换言之就是4个参数中最难实现精确反演的，这也是散射＋透射信号在10%高斯噪声下，相对误差唯一超出范围的参数。绘出并对比各个情况下的粒径分布函数后（见图6）发现，μg对分布函数的影响没有σg大，即使其相对误差达到3.75%，但只要σg反演结果足够精确，反演得到的分布函数与真实的分布函数也几乎相同。而如果σg反演结果不够准确（仅使用散射信号的情况），分布函数的曲线就很明显偏离了真实的分布曲线。因此可以认为，在10%高斯噪声下，同时使用散射和透射信号得到的反演结果也达到了精确级别。

值得一提的是，CMA-ES算法为本文方法带来收敛速度上的优势。图7展示了不同高斯噪声下，采用散射＋透射信号的反演过程中适应度函数值的下降过程（分别是50次计算中具有代表性的一次，其余49次的下降情况也基本相同）。迭代上限是1 000，无高斯噪声的情况下因达到目标精度而提前结束反演过程。而在6%和10%高斯噪声的干扰下，500代之后也基本平稳不再明显下降，因此只展示了前450代的收敛过程。从中可以发现，3种高斯噪声下，250代以内都很迅速地完成收敛过程，250代时平均耗时为3.5 s。250代之后，对于无干扰的情况，曲线会迅速降到目标精度使反演结束。而高斯噪声的存在使另外2种情况只能降到一个相对最小值，并在该值附近微弱地波动，实际上有效的反演过程已经完成，余下迭代过程只是在等待迭代次数达到上限。由于算法的特点，计算时间是与迭代次数成线性正比，450代时平均计算耗时6.3 s。在大量数值模拟的结果基础上，认为可以将最大迭代次数缩小到450代，以减少无效的计算时间提高效率。虽然3.5 s的计算用时还不足以到达在线测量的要求，但是也为接下来研究工作提供了良好的基础。

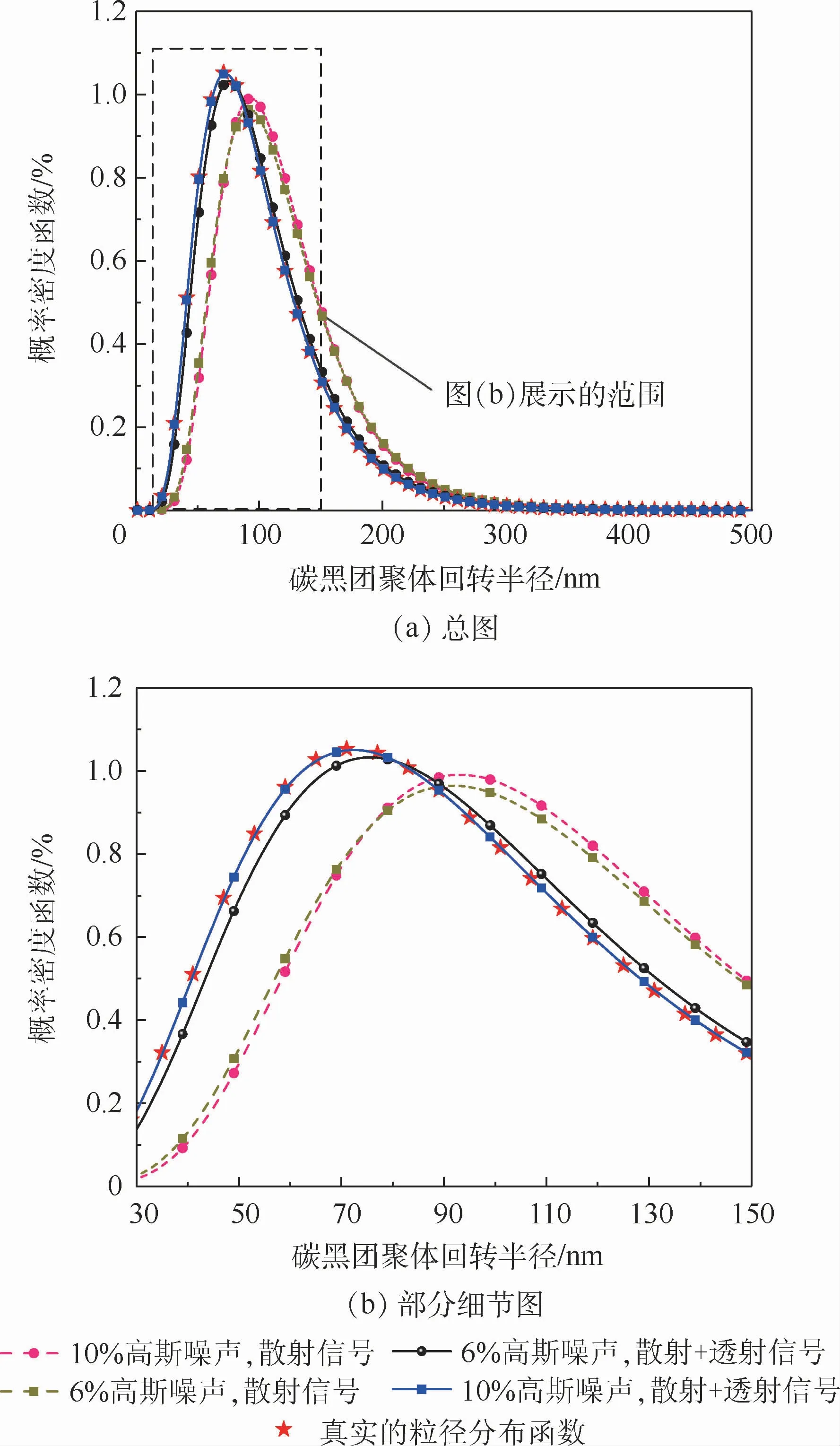
图6 不同高斯噪声下使用不同信号方案反演得到的粒径分布曲线Fig.6 Particle size distribution profiles obtained by inversion results of different signal schemes under different Gaussian noise

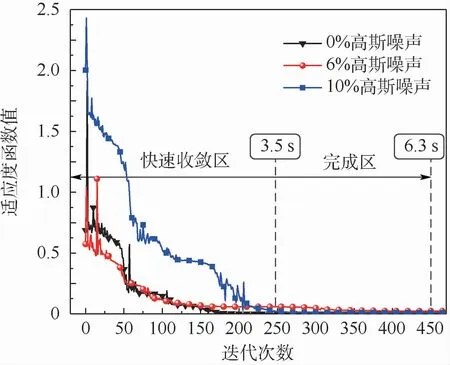
图7 不同高斯噪声下散射-透射组合信号的收敛过程Fig.7 Convergence process of scattering-transm ittance combined signal under different Gaussion noise

4 结 论

数值计算结果证明了本文提出的在一定高斯噪声下精确并且稳定地用于同时重建碳黑团聚体粒径分布、分形维数和常数参数方法的可行性。这一结论在于：对比在相同高斯噪声下只使用散射信号的4个参数的反演结果，采用散射-透射信号组合的反演结果更好，即4个参数各自的反演相对误差明显降低，各自的标准差缩小。尤其是随着高斯噪声的增加，反演的结果精度达到了可以忽略的范围（小于1%），实现精确反演。

1）散射-透射信号改善了反问题的病态性，并在10%的高斯噪声下实现碳黑团聚体的形态和粒径分布参数的精确同时反演。

2）使用CMA-ES算法使得反演过程迅速收敛，初步达到3.5 s内基本完成反演过程的效果。

3）本文得到的数值结果是在很大的目标参数搜索空间下得到的，这些范围在其数学意义和参数自身性质上都足够大，因此该方法的大搜索范围普适性可以得到验证。