基于复杂网络的空中交通复杂性识别方法

吴明功，叶泽龙，3，温祥西，*，蒋旭瑞

（1.空军工程大学 空管领航学院，西安710051； 2.国家空管防相撞技术重点实验室，西安710051；3.中国人民解放军95178部队，南宁530049； 4.中国人民解放军94116部队，和田848000）

随着空中运输的需求不断增加，空中交通管制面临着日益增加的复杂性的挑战。冲突探测和解脱（Conflict Detection and Resolution，CD＆R）技术，旨在警告飞行员即将发生飞行冲突，并协助其执行避让动作，以减轻空中交通管制员工作压力。因此，近年来，人们不断开展对CD＆R技术的研究。空中交通系统是一个复杂系统，随着航空器数量不断增加，当飞行量超过空域容量的上限，将导致空中交通拥堵的现象，影响飞行效率，甚至演变为飞行冲突，危及飞行安全。因此，本文认为空中交通拥堵实际上是飞行冲突的早期表征。研究空中交通态势评估，即空中交通拥堵识别，对于评价飞行安全质量具有重要意义。对飞行冲突进行早期预警和预先调配，并提供决策支持和参考依据，是战略型冲突探测中的重要内容，是中期冲突探测系统（Medium-term Conflict Detection system，MTCD）中的先期告警平台［1］。

随着空中交通态势在许多因素的综合作用下变得异常复杂，许多问题在还原论思想的指导下得不出合理的解释。在这一时期，复杂性科学蓬勃发展，人们开始利用复杂性理论研究空中交通态势。Prandini等［2］考虑了飞机预测航迹的不确定性，提出了通过概率型的空域使用率评估3-D空域的空中交通复杂度算法，为战略冲突解脱提供机动策略。张进等［3］认为空中交通复杂性贯穿于空中交通管理的始终，已成为认识系统涌现的重要线索。张晨等［4］提出了基于连携效应的交通复杂性测度模型，改进了扇区范围内的改航航段和策略生成方法。

上述研究从宏观角度评估了空中交通的复杂性。宏观指标往往通过对航空器较多的繁忙时段采集获取，是对一段时间的统计信息，缺乏实时性。此外，尽管此类数据较易获取和应用，但是由于运行环境的差异导致数据缺乏普适性。在空域中，飞机之间的相对位置关系能够实时地反映当前空域中的冲突情况和调配难度即空中交通的复杂性。从这个角度出发，一些研究者建立了飞机状态网络，并用复杂网络理论评估空中交通的复杂性。陈新伟等［5］构建了基于复杂网络理论的航线飞行CD＆R的基本框架。王红勇等［6-7］中以节点度、连通率和网络结构熵描述网络复杂性，提出以内聚力和稳定性指标反映飞机聚集成簇的程度。Zanin［8］以K-means聚类算法划分空域交通复杂情况。复杂网络分析方法为本文揭示飞行状态网络结构提供了重要的理论工具，为了描述网络结构特性，需要选择反映网络全局特性的复杂网络指标。

以上文献中构建的网络是无权网络，丢失了距离信息，且选择的指标对网络结构信息反映不全面。为了对空中交通复杂性进行综合分析，本文从复杂网络的角度描述了空中交通状况，并采用了一些新的指标进行识别。此外，评估方法也是复杂性识别中的关键问题。经典的评估方法往往需要主观设置阈值，聚类算法同样在很大程度上受类别数k的影响。为了解决上述问题，本文提出了一种空中交通复杂性识别的黑盒方法，通过对样本的学习直接找出复杂性识别的控制限，避免了阈值设置上的主观性。首先对空中交通状况进行飞行状态网络建模，选取了5个静态拓扑指标映射空中交通复杂性，然后引入独立主元分析（Independent Component Analysis，ICA）方法对空中交通复杂态势进行在线监控［9-11］。通过本文所提方法，可以实时获取空情信息，分析空中交通态势及其演化过程，为战略层飞行冲突预警提供决策支持。通过人工网络和实际飞行状态网络验证了所提方法的有效性。

1 飞行状态网络建模方法

1.1 网络的构建

以飞机为节点，当潜在冲突发生时，飞机通过机载防相撞系统（Airborne Collision Avoidance System，ACAS）与邻机通信，并立即采取行动解决冲突。如果ACAS通信距离的范围覆盖了邻近的飞机，则节点之间有一条边。这里，ACAS通信距离RACAS＝40 km。飞行状态网络结构差异性如图1所示。

图1中，相同的空域内分布着5架同型航空器，其ACAS通信距离均为40 km，3个空域按照复杂程度从小到大排序依次为：空域A、空域B、空域C。图1（a）中，各飞机在空域中分布相对分散，反映在复杂网络中即为各节点相互孤立；图1（b）中，部分飞机相互靠近聚集成簇，在彼此ACAS通信距离内，开始构成连边；图1（c）中，所有飞机聚集在空域的中心区域，空中态势拥堵程度高，网络全连通甚至出现环边，极不利于管制员调配冲突。

此外，航空器间的距离直接影响飞行安全，本文设想将距离因素也考虑进飞行状态网络内。当两机间隔越小，冲突越突出，网络也越紧密。因此，本文将两机距离的倒数设置为网络边权，将上述模型拓展为加权网络模型，其权值设置如图2所示。

当两机距离d＝35 km时，两机ACi和ACj连边的边权为wij＝1／35。由此看出，当空域中航空器数量相当时，空中交通复杂性受网络结构影响很大。

图1 飞行状态网络结构差异性Fig.1 Difference of flight state network structures

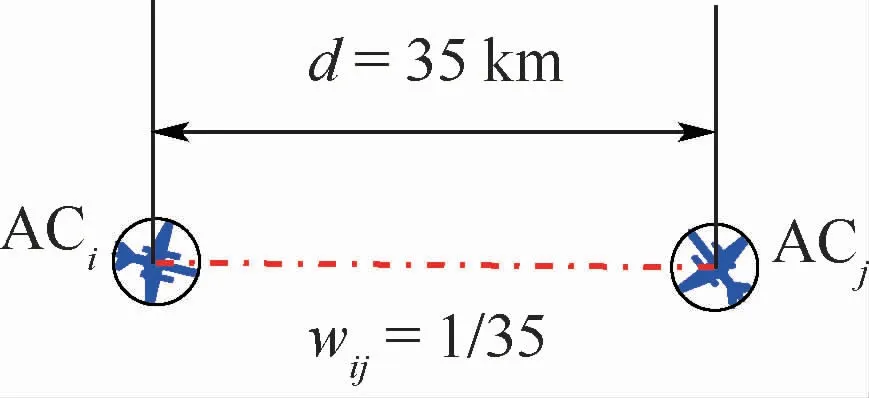
图2 边权设置Fig.2 Edge weight setting

2）在线监控阶段

步骤1 以待监测的数据为测试集，进行预处理。

步骤2 在线计算监测数据的SPE、I2和统计量，评估空中交通复杂性。

步骤3 若某统计量大于对应控制限，则认为该采样时刻空中交通拥挤；否则认为空中交通流畅。

4 仿真分析

为了验证本文方法的有效性，首先对空中交通态势进行仿真，考察在仿真环境中的监测效果；其次以ZPPP-昆明长水机场进近阶段数据为监测样本，对某日15：40—16：05期间的空中交通情况进行动态评估。

4.1 数据采集

在仿真场景中，空域大小设置为200 km×200 km。为了方便描述空域飞机分布情况，随机产生一批飞机但其位置服从特定分布，且从样本多样性角度考虑，本文假设飞机位置服从均匀分布、正态分布和指数分布，且x、y坐标值之间相互独立。首先，本文认为飞机（节点）数对空中交通复杂性影响最大，这在飞行状态网络结构中能够体现。以飞机位置服从均匀分布为例，节点数N＝40，80，其网络结构变化可如图4所示。

固定空域中，当节点数很少时，如图4（a）所示，节点之间相互连接，但网络仍不是全连通的；当节点数量增加到80时，如图4（b）所示，网络全连通，且随着飞机数量的增多，网络规模进一步扩大。经过大量测试发现，该空域中节点数N＝40时，空中交通仍比较流畅，结论的依据是大部分样本中的飞行冲突数量都小于5。这里，二维平面中飞行冲突定义为两机间隔小于5 min。因此，本文采集节点数N＝20，30，40且服从均匀分布的样本各50组，作为正常数据集。飞机位置服从均匀分布是一种空域利用率最高的理想状态，一般情况下，民航飞机按照机场-进近-区域飞行，军航飞机根据作训任务的不同，灵活选择空域或航线，鲜有文献对位于空域中的飞机位置分布规律进行统计分析。这里，为了方便描述，本文假设飞机位置服从正态分布和指数分布，且节点数均为N＝80，网络结构如图5所示。

图4 网络结构随节点数增多的变化情况Fig.4 Variation of network structure with increase of node number

与图4（b）相比，同样是80个节点，节点之间紧密程度由强至弱依次为：指数分布，正态分布，均匀分布。特别是飞机坐标服从指数分布时，大量飞机聚集在中心位置，飞行冲突突出，空中交通复杂程度过高，拥挤严重。本文以这2种情况的样本为在线监测测试集，逐渐减少节点数，考察提出的方法对空中交通拥堵识别的效果。

在实际飞行场景中，本文以ZPPP-昆明长水机场进近阶段数据为样本，选择交通流畅的样本训练后，对某日15：40—16：05期间的空中交通情况进行了动态评估。每隔5 m in，以快照（Snapshot）的形式记录下实时的空中交通情况，这样动态复杂网络被离散为6个静态子网络（Sub-networks），通过提出的方法对空中交通状况进行在线监控。

4.2 仿真场景

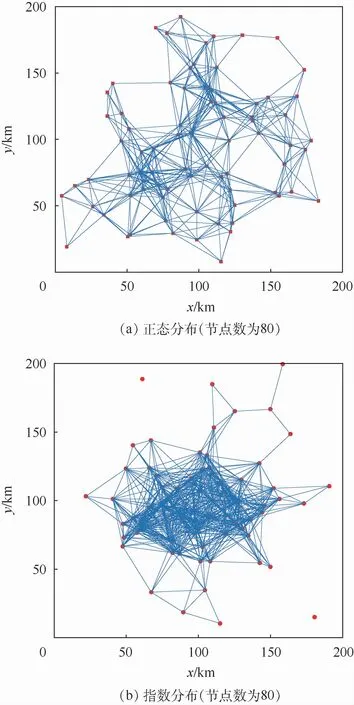
图5 相同节点数不同分布时网络结构的差异Fig.5 Difference of network structure with the same node number but different distribution of nodes

首先，本文从静态子网络的角度出发，考察该方法的有效性。即在空域中随机产生一批飞机，记录下此时的飞机位置信息，收集若干样本作为测试集，在离线训练好的模型中在线监测。采集飞机数量N＝20，30，40且服从均匀分布的样本各50组，作为正常数据集，且这些数据中飞行冲突数量均小于5。首先，本文探究所提方法在飞机数量增加时对空中交通拥堵的识别效果，测试集为服从均匀分布的50组节点数量均为N＝50的样本，其中，飞行冲突数量均大于8。前150个样本为正常数据集，后50个样本为监测数据集，其结果如图6所示。

从图6中可以看出，提出的方法能够准确识别空中交通异常。I2和Ie2统计量从第151个样本开始监测到异常，不存在延迟和错误诊断。SPE统计量在训练过程中不稳定，导致控制限偏高；在监测阶段，从第151个样本起虽然SPE统计值明显高于训练阶段统计值，但大部分仍略低于控制限，未能判断为拥挤样本。

为了进一步说明是何种原因造成了交通拥挤，本文给出第175个样本的贡献图，变量1～5依次为环边数、平均点强、平均加权聚类系数、平均点介数和网络效率指标，结果如图7所示。

图6 监测图（均匀分布且节点数为50）Fig.6 Monitoring charts（uniform ly distributed and node number equals to 50）

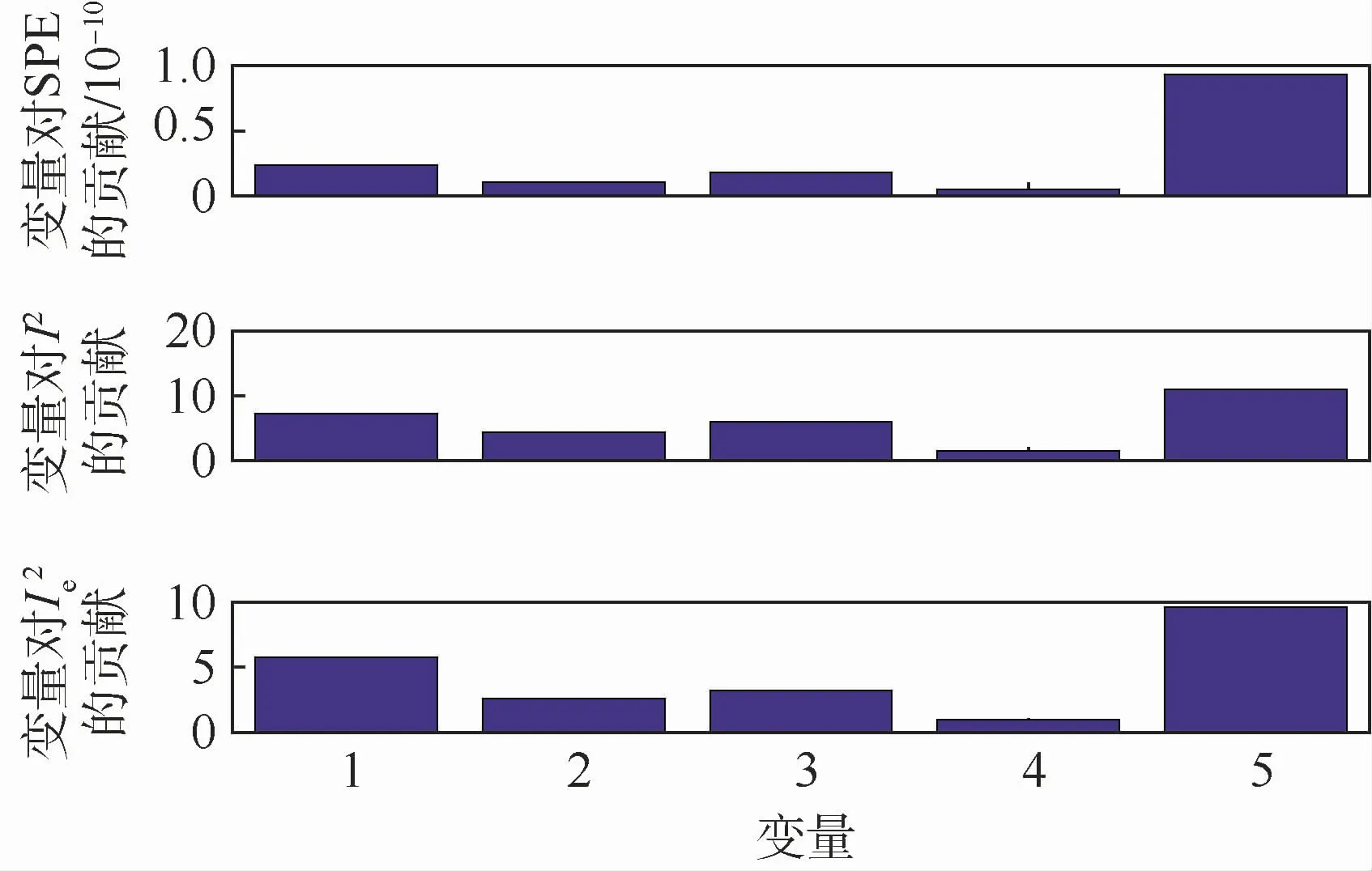
图7 变量对偏差的贡献Fig.7 Contribution of variables to deviation

从图7中可以看出，网络效率对空中交通拥堵影响最大，其次为环边数、平均加权聚类系数和平均点强，平均点介数最弱。这是因为随着空域中飞机数量的不断增加，网络结构趋于复杂，这些从网络整体复杂度出发的指标最为敏感，而由于网络结构类似于随机网络，平均点介数和平均加权聚类系数指标相对变化较小。

另外，本文比较关心该方法在不同网络结构中的效果，这里以飞机坐标服从正态分布和指数分布的样本为测试集，训练集同上一试验。由于这2种情况下交通状态明显拥堵，本文设置空域中的飞机数量与训练集中相当，N＝40，30，20，考察方法对复杂性的评估能力，监测结果如图8所示。

图8 不同节点数和分布时的监测图Fig.8 Monitoring charts with different node number and distribution

图8（a）～图8（c）服从正态分布，图8（d）～图8（f）服从指数分布，且各组样本中节点数量从40依次减少到20，监测样本中飞行冲突数量均大于8。当飞机位置服从正态分布且节点数量N＝40和30时，如图8（a）、图8（b）所示，拥堵情况被部分统计量准确识别，验证了该方法对于不同结构的有效性。当节点数量减少到20时，如图8（c）所示，I2统计量的控制限因训练阶段的一个错误样本而严重偏高，而SPE和Ie2统计量的监测样本与训练样本存在比较明显的差异，在控制限上下波动，空中交通已经比较流畅。当飞机位置服从指数分布时，如图8（d）、图8（e）和图8（f）所示，拥挤情况均被所有或部分统计量识别出来。特别图8（f）与图8（c）相比，虽然节点数均为20，但指数分布的异常情况被SPE统计量识别出来，说明了相同飞机数量的情况下，指数分布比正态分布更加拥挤。上述试验验证了该方法对于静态网络的复杂性识别有效性，样本中各网络相互独立，没有时间上的先后顺序。

4.3 空管运行场景

在实际空管运行场景中，本文以ZPPP-昆明长水机场进近阶段数据为样本，对某日15：40—16：05期间的空中交通情况进行动态评估。每隔5 min，以快照的形式记录下实时的空中交通情况，这样动态复杂网络被离散为6个静态子网络，如图9所示。

进近阶段空中交通态势如图9所示，一个动态复杂网络按照相同的时间间隔5 min离散为6个静态子网络，客观反映了空中交通态势的动态变化过程。通过复杂网络建模，雷达管制实况可抽象为如图10所示的网络结构图。

从图10可以比较直观地看出，随着将飞机从进近阶段向机场管制区域移交，空中交通态势的总体趋势从拥挤逐渐转变为流畅。然而，本文需要一种研究方法对空中交通复杂性进行定性的分析。因此，本文在该场景下验证提出方法的有效性。为了获得理想的监测效果，本文将管制区容量考虑在内，在大量的真实数据中选择了50个交通流畅的正常样本作为训练集。在表1中列出了部分样本的5个拓扑指标。通过核密度估计方法计算出的SPE、I2和统计量的控制限分别为3.3357×10-29、15.3452和9.752 1。在异常监测阶段，6组样本的拓扑指标和对应的SPE、I2和统计值如表2所示。

图9 进近阶段不同时刻雷达屏幕截图Fig.9 Radar screenshots at differentmoments in phase of approaching

图10 进近阶段不同时刻离散子网络Fig.10 Discrete sub-network structures at differentmoments in phase of approaching

将监测样本统计值与控制限比较，本文发现SPE和I2统计量识别到了部分异常情况，而统计量总是低于控制限。SPE统计量判断前4个样本为拥挤态势，而I2统计量识别到前2个样本为拥挤态势，说明SPE统计量相较于I2统计量对指标的变化更加敏感。在这6个采样时刻中，根据SPE和I2统计量的评估结果，态势从拥挤到流畅的复杂性排序均为：1＞2＞3＞4＞6＞5，差异仅在于2个统计量对于指标变化的敏感程度。因此，本文认为在进近区域的空中交通复杂性识别中，在判断空中态势是否拥挤时，SPE和I2统计量都应给予充分关注。为了验证提出方法的评估效果，利用文献［19］中的聚类算法测试同样的管制运行数据，与本文方法进行比较。文献［19］将不同维度和阶段的拓扑指标组合成一个综合复杂性指标向量，使用K-means算法将样本依据空中交通复杂性划分为3类。各指标和评估结果如表3所示，表中：Ei，j为第i层第j级的 边数，Ci，j为该层级的聚类系数。

从复杂性评估等级可以看出，前2个样本被识别为“高”等级，第4个样本为“中”，其余样本为“低”，复杂性的总体变化趋势与所提方法的结果几乎相同，但个别样本的结果存在差异。从方法的角度看，聚类算法缺乏训练过程，因此获得的复杂性等级是相对测试样本自身而言的。该模型受类别数k的影响；而在提出方法中，控制限是通过大量顺畅样本训练获得的，复杂性评级对指导飞行活动更具有参考意义。从仿真结果看，聚类算法认为第3个样本复杂性等级为“低”，第4个样本是“中”，但所提方法识别出前4个样本为复杂样本，且等级从高到低依次为：1＞2＞3＞4＞6＞5。从图10中可以看出第3个样本的复杂性明显比第4个更高。在类别数k＝2的条件下再次测试，此时，前4个样本被评价为“高”，后2个样本被评价为“低”，结果与所提方法相同。此试验说明了聚类算法受类别数k的影响较大，进一步验证了此方法的有效性与鲁棒性。

表2 监测样本拓扑指标值和SPE、I2 和统计值Table 2 Topological ind icator values of m onitoring sam p les and statistic values of SPE，I2 and

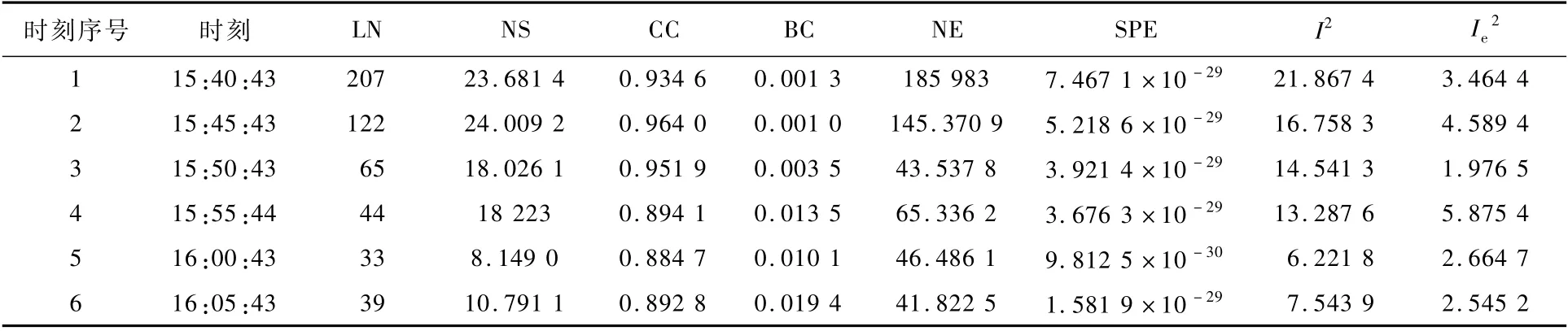
表2 监测样本拓扑指标值和SPE、I2 和统计值Table 2 Topological ind icator values of m onitoring sam p les and statistic values of SPE，I2 and

2时刻序号 时刻 LN NS CC BC NE SPE I2 I e 1 15：40：43 207 23.681 4 0.934 6 0.001 3 185 983 7.467 1×10-29 21.867 4 3.464 4 2 15：45：43 122 24.009 2 0.964 0 0.001 0 145.370 9 5.218 6×10-29 16.758 3 4.589 4 3 15：50：43 65 18.026 1 0.951 9 0.003 5 43.537 8 3.921 4×10-29 14.541 3 1.976 5 4 15：55：44 44 18 223 0.894 1 0.013 5 65.336 2 3.676 3×10-29 13.287 6 5.875 4 5 16：00：43 33 8.149 0 0.884 7 0.010 1 46.486 1 9.812 5×10-30 6.221 8 2.664 7 6 16：05：43 39 10.791 1 0.892 8 0.019 4 41.822 5 1.581 9×10-29 7.543 9 2.545 2

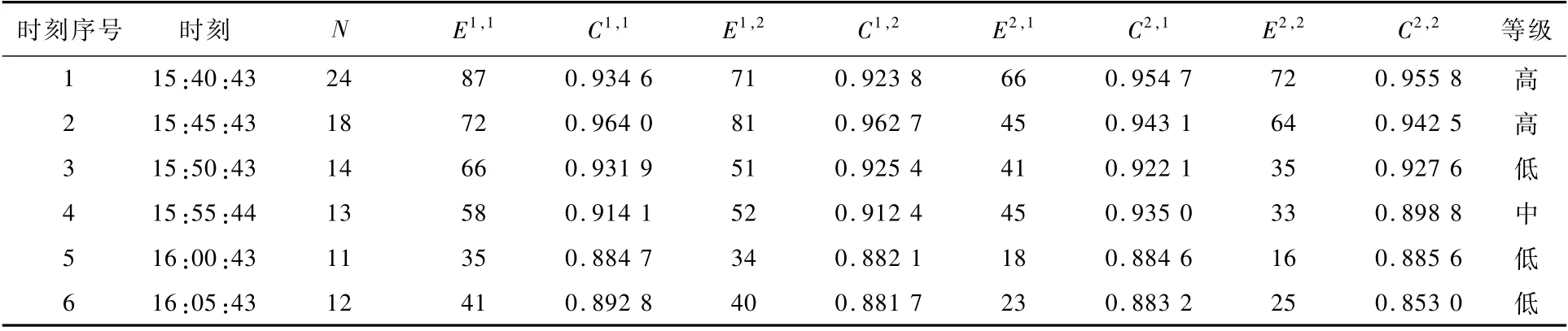
表3 文献［19］中K-m ean算法对相同样本的复杂性识别结果Tab le 3 Com p lexity recognition resu lts of K-m ean algorithm for the sam e sam p le in Ref.［19］

5 结 论

1）针对战略层面冲突探测与解脱特点，本文提出了一种基于复杂网络分析和ICA异常监测算法的空中交通复杂性识别方法，弥补了中期冲突探测系统对空中交通态势整体评估的不足。

2）通过构建飞行状态网络，利用拓扑指标与空中交通复杂性建立映射关系，选择的指标能够较全面地刻画网络结构和性能，为了客观地评估空中交通状况，引入了ICA监测的黑盒方法，通过训练交通顺畅样本计算控制限，将测试样本的SPE和I2统计量与控制限比较来识别复杂情况，克服了其他评估方法阈值设置的主观性问题。

3）在仿真场景和管制运行的真实场景中，3个统计指标从不同角度反映复杂性，互为补充，较好地监测空中交通态势，方法稳定性、普适性较强。

本文方法仅从空域的情况分析了空域中的交通复杂情况，空域情况是相对管制员而言的。因此，后期结合管制员的管制难度和工作负荷对空域复杂性进行分析，将能够更有针对性的体现空中交通情况。