基于BiasSVD 和聚类用户最近邻的协同过滤算法研究
李佳,张牧
(成都体育学院,成都 610041)
0 引言
随着网络科技的发达,信息泛滥的时代已经到来,一般的搜索引擎不能为用户提供准确的搜索结果,而个性化推荐系统能够主动学习与分析用户的行为,自主对信息过滤,为用户提供适合自己需求的推荐。个性化推荐系统的算法有多种,其中协同过滤算法是最成熟的[1],面对如今的大数据时代,协同过滤算法存在可扩展性问题。Sarwar 等人[2]将SVD 技术运用到协同过滤算法,得到低秩矩阵,降低矩阵复杂度。Rashid 等人[3]采用聚类技术为每个聚类生成代理用户,与目标用户相似度最高的代理用户进行最近邻的推荐,大大减小对最近邻的搜索范围。Karypis 等人[4]指出通过增加服务器数量,提高算法吞吐量。李改等人[5]在SVD 模型中进行正则化约束来训练数据,用最小二乘法来训练分解模型。
为了解决协同过滤算法的可扩展问题,本文提出基于BiasSVD 和聚类用户最近邻的协同过滤算法,首先选用的是BiasSVD 降维技术,该方法在原有的LFM模型上加入偏置项,使得BiasSVD 模型更加贴近现实和精细,该方法对扩展性的问题改善程度较为显著,但是仍然会造成信息丢失以及存在一定的偏差,所以最终得到的目标用户预测评分将通过聚类用户最近邻预测评分和真实评分的平均偏差值来调整,从而提高协同过滤算法的推荐质量。
1 相关工作
协同过滤算法为用户产生推荐大概分为三个步骤,通过自主收集学习用户行为信息,建立用户项目评分矩阵Rm×n,接着计算用户或者项目之间的相似度产生最近邻集合,最后根据最近邻产生预测评分或者商品推荐。
本文评分矩阵有m行n列,m代表用户个数,n代表项目个数。其中,u、v表示用户,i、j表示项目,rui为用户u对项目i的评分。
1.1 BiasSVD
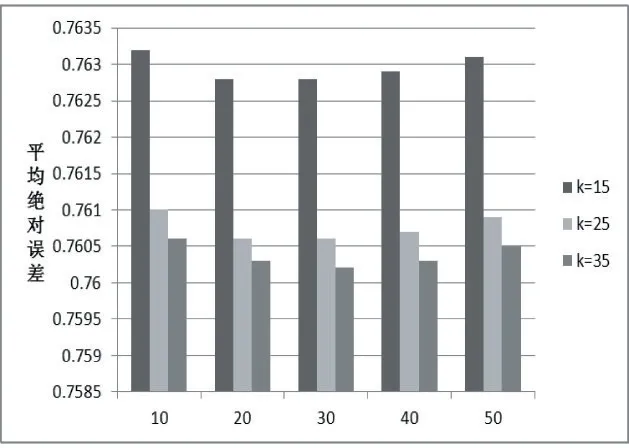
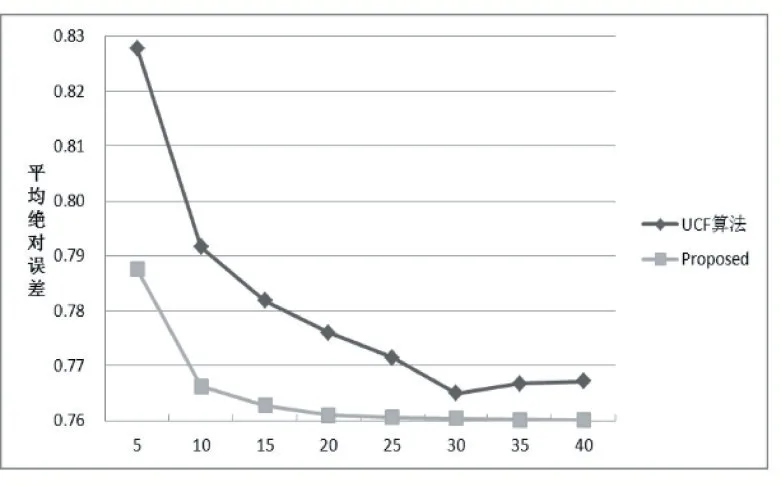
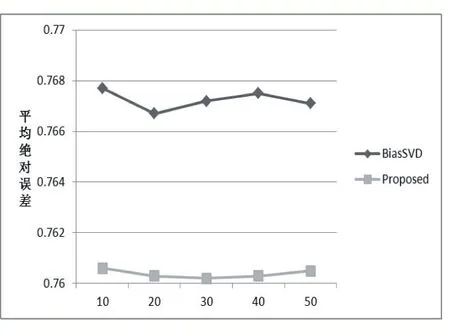
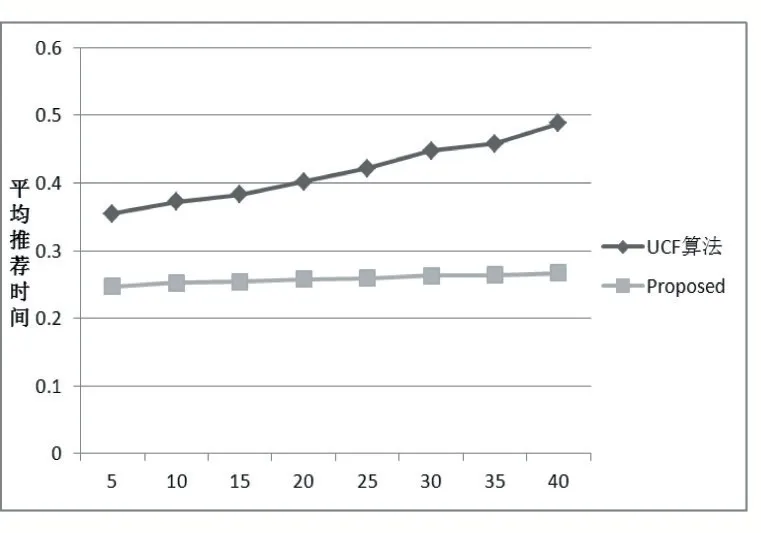
BiasSVD 又叫偏差矩阵分解[6],它是通过降维的方法把高维的项目评分矩阵Rm×n分解为两个低维矩阵相乘,即Rm×n=Pm×fQf×n,其中f bui为用户u对项目i的偏好评分,μ为数据训练集中所有评分记录的平均值,bu[u]表示用户u评分偏差,bi[i]表示项目i的偏好。 例如预测用户Grace 对《计算机导论》这本书的偏好评分,其中总体平均值为3 分。《计算机导论》的质量比大部分书籍都好,对它的评分比其他书籍平均分高于0.6 分。而且用户Grace 评分是比较严谨的,偏向于给书籍打低0.2 分,所以用户Grace 对《计算机导论》的偏好评分bui=3+0.6-0.2=3.4。从上述分析,利用偏差矩阵分解的评分预测公式如下: pui为用户u对项目i的预测评分,p和q表示经过降维后的用户特征矩阵以及项目特征矩阵。 基于BiasSVD 预测出来的评分加上偏置项,不仅降低数据复杂度,而且使得预测评分更接近真实评分,但是依然存在一定偏差,需要通过最近邻用户真实评分和预测评分的平均差值来调整目标用户的预测评分。 聚类的方法有很多种,本文采用的是K-means 聚类方法。基于K-means 聚类协同过滤算法首先确定k个聚类中心,然后计算用户与每个聚类中心之间的相似度,比较这些相似度的大小,用户就和相似度最高的聚类中心是一个类别的,以此反复计算,直到所有用户都已经聚类,最后为目标用户寻找最近邻,第一步是计算目标用户和聚类中心的相似度,找到目标用户所属类别,第二步就是在该类别的集合中找到目标用户的最近邻,由此可以看出,最近邻的搜索空间已经大大地减小。 在该聚类的集合中计算用户之间的相似度,本文选取的用户相似度公式是在皮尔逊系数基础上作了一点改进。皮尔逊系数公式: 公式(3)中计算目标用户u与用户v相似度,ruv表示用户u与v共同评分的项目集合。rui和rvi分别表示用户u和v对项目i的评分,分别表示用户u和v评分平均值。 公式⑷是改进的相似度公式,N(u)⋂N(v)表示用户u和v共同评分个数,N(u)⋃N(v)表示用户u和v评分项目数的并集。这在一定程度上惩罚共同评分项目数少的用户相似度,提高相似度计算的准确性。 通过公式(4)计算目标用户u和其他用户v的相似度sim(u,v),相似度大小取值范围为[-1,1],然后降序排列,选取前N 个作为目标用户u的最近邻集合。 本文提出的基于BiasSVD 和聚类用户最近邻的协同过滤算法的中心思想是通过公式(2)得到预测评分pui,然后采用公式(4)计算相似度获取目标用户u最近邻集合user(u),最后结合最近邻真实评分rvi与预测评分pvi之间差的平均差值evi来调整目标用户的最终预测评分即公式如下: 其中 N 是集合 user(u)的元素个数,eui相当于是一个偏移量。当eui的值大于零时,表示实际上真实评分比预测评分高很多,所以增加偏移量eui到原来基准评分pui上;当eui值为零时,表示预测出来的评分已经很精确接近真实评分,不需要再调整;当eui值小于零时,真实评分比预测出的评分低很多,相应的在基准分pui上减去偏移量evi。所以最终预测评分公式如下: 为了得到最合适的用户、项目特征矩阵p、q和用户、项目偏好向量bu、bi,利用随机梯度算法来优化,首先定义误差公式由于防止过拟化加上规范化因子最终误差公式如下: 公式(8)利用随机梯度下降法得到的更新规则为: 算法2 基于BiasSVD 和用户最近邻的协同过滤算法 输入:项目评分矩阵Rm×n,目标用户u,项目i,用户项目特征数f,迭代次数step,以及梯度下降步长γ,惩罚因子λ 输出:用户u对项目i的预测评分 步骤: (1)计算总体平均值μ (2)初始化bu、bi为全 0 (3)初始化p、q矩阵 (4)过随机梯度下降法的迭代得到优化好的p、q矩阵和bu,bi向量 (5)对所有用户进行K-means 聚类 (6)通过公式(5)计算evi的值 (7)找到目标用户聚类的集合,基于该集合利用公式计算p'ui预测评分 为了验证改进算法的准确性,首先应该选择合适的数据集,本文采用的数据集是由美国Minnesota 大学的GroupLens 研究小组从MovieLens 网站提取而来[7]。该数据集有943 个用户,1682 部电影,总共有100000条记录,每个用户至少要为20 部电影评分,分值范围是1-5,分数高低表示用户对电影的喜好程度。数据集分为训练集和测试集,按80%和20%的比例来分。 评分预测的预测准确度一般用均方根误差(RMSE)和平均绝对误差(MAE)计算[8]。本文采用MAE 作为本实验的评价标准,它是通过计算用户实际项目的评分与相对应的预测评分之间的绝对偏差和的平均值表示预测准确度,其值越低,预测准确性则越高。公式如下: pi、qi分别表示用户对项目i的预测评分和实际评分,N表示项目的个数。 平均推荐时间(MRT)反映了产生推荐项目的时间,其计算公式如下: Tis为用户发出请求的时间,Tic用户得到的推荐结果。 在本文实验中,随机梯度下降法的梯度下降率为0.99,迭代次数step=100,参数值γ=0.02,λ=0.3。 实验1:不同特征向量维度下不同近邻数的比较结果 图1 特征矩阵维度f 与近邻数量k 的关系 由图1 观察知道随着特征矩阵维度f的增加,不同近邻MAE 值的也在减小,并且随着最近邻数k的增加,预测精度也在逐渐提高。 实验2:不同近邻数k比较结果 从实验1 得到特征矩阵维度f的取值影响着MAE 值的大小,本实验中在f=30 基础上,观察不同最近邻数的MAE 值大小,并且与基于用户的协同过滤算法(UCF 算法)作比较。 图2 改进算法与UCF算法MAE值比较结果 由图2 可知在f=30 基础上,随着最近邻数k的增加其MAE 值也在减小,预测准确度在提高。但是当k的值过大,导致算法复杂度增加,并且准确度也会降低。改进的算法MAE 值均小于基于用户协同过滤算法MAE 值,说明改进算法提高了预测准确度与推荐质量。 实验3:基于BiasSVD 与改进算法的比较结果 从实验2 可知当最近邻数取值适当时,改进算法的预测准确度比较高。本实验在k=35 的基础上,比较本文改进算法(Proposed)与基于BiasSVD 协同过滤算法的准确度。 图3 改进算法与BiasSVD算法的MAE值比较 由图3 观察得到改进的算法的MAE 值比基于Bi⁃asSVD 协同过滤算法MAE 值都要小,说明改进的算法在一定程度上提高推荐算法的预测准确度,从而提高推荐系统的推荐质量。 实验4:不同算法平均推荐时间比较 图4 改进算法与UCF算法的平均推荐时间比较 由图4 可知,本文改进算法的平均推荐时间都要少于基于用户的协同过滤算法,所以改进算法大大缩减了推荐时间,在一定程度上提高了算法的扩展性。 本文针对协同过滤算法可扩展性问题,在偏置矩阵模型基础上结合聚类用户最近邻实际评分与预测评分之间的平均偏差来调整目标用户的预测评分,从而不仅减低数据的复杂度,并且提高了评分预测的准确性,以及可扩展性。

1.2 聚类用户最近邻
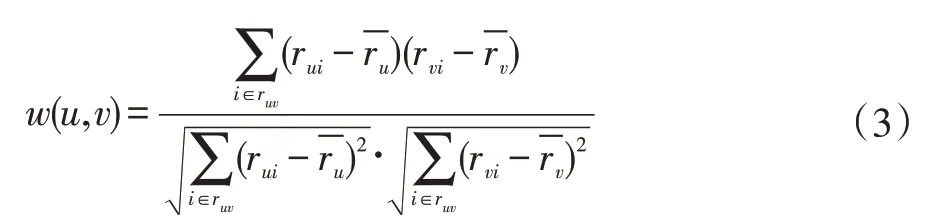

2 基于BiasSVD和聚类用户最近邻的协同过滤算法

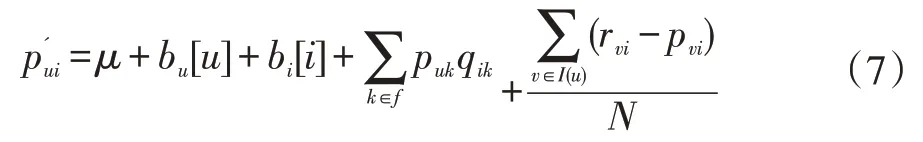
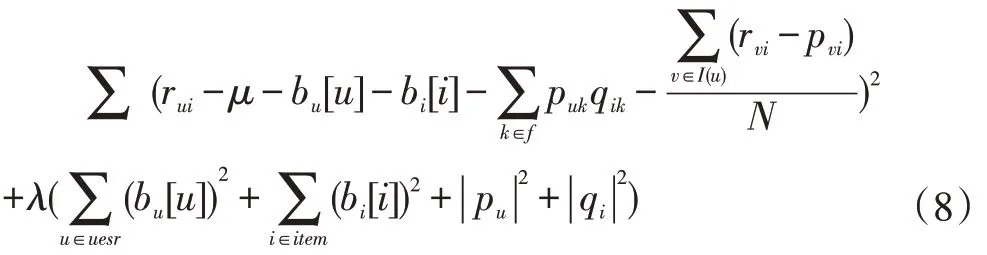
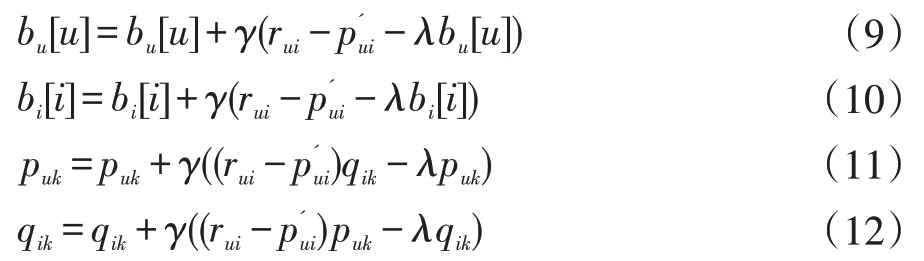
3 实验结果及分析
3.1 实验数据集
3.2 评价标准


3.3 实验结果及分析
4 结语

