政治生态评价指标体系的构建

王媚，刘广聪

（广东工业大学计算机学院，广州 510006）

0 引言

随着习总书记在中央纪委二次全会中首次提出“政治生态”概念并在后续的多次党代会[1-2]中加以强调后，“政治生态”逐渐成为了党政机关关注的焦点，加快和推进政治生态建设成为了执政发展的必然趋势和必然要求。政治生态反映的是责任主体的政治生活情况，它直接影响着从政环境的优良，因此，构建合理的评价体系来观测政治生态状况，为研判提供依据，势在必行。

层次分析法（Analytic Hierarchy Process，AHP）[3]是美国运筹学家萨蒂于20 世纪70 年代初，提出的一种层次权重决策分析方法，它将与决策有关的元素分解成目标、准则等层次，并在此基础之上进行定性定量分析，该方法的特点在于对复杂决策问题的影响因素进行深入分析，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则、无结构特性的复杂问题提供简便的决策方法[4]。在政治生态研判的过程中往往需要考虑很多方面的因素，而这些因素总是相互制约、相互影响，彼此之间往往很难用定量的方式进行描述。为顺应党政部门政治生态建设的形势和现实需要，本文采用群组决策和层次分析相结合的方法来构建政治生态评价指标体系。通过该方法的引入，有效地将政治生态问题做了层次分解，逐层比较各因素的相对重要性，为最终的政治生态研判提供科学合理的定量依据。

1 研究现状

国外对政治生态的研究起步比较早，最开始的时候学者们主要研究生态环境问题，到了20 世纪80 年代，人们开始思考造成这些生态问题的原因是什么，哪些社会原因、经济原因对此造成了影响。慢慢的人们开始研究绿色政治，对于良好政治生态的需求日益增强，期待社会的公平、人权的平等、生态的和谐。

国内关于政治生态的研究则起步较晚，早期仅在西方研究的基础上进行探索，但随着近几年国家多次提出和强调要营造廉洁从政的良好环境，政治生态开始慢慢被重视起来，逐渐成为了研究的热门话题。这一时期学者们研究的课题多与党政建设密切相关，具有较强的针对性和问题导向性。对于政治生态的优化和构建，许多学者纷纷提出了自己的看法和见解，刘守旗[5]认为要加强党的思想建设，陈朋[6]认为要严肃党内政治生活，刘峰[7]认为要坚持正确的用人导向等[8-23]。

国家虽多次提及各级党政机关和部门要优化从政环境，但未明确指出优化的方向和标准，目前的政治生态体系建设仍处于不断探索和研究的阶段，需要学者们不断的推陈出新、革故鼎新，寻找出最符合当前环境下的研判体系。本文依据我国政治生态建设的实际情况、分析党政部门从政环境的现实特征，基于群组决策[8]和层次分析方法构建适用于党政部门的政治生态评价指标体系，旨在更科学、更合理的研判从政环境，协助提升执政能力。

2 指标体系构建

2.1 层次结构模型

本文从政治生态的内涵出发，遵循体系构建的科学性、合理性、可操作性等原则，结合党政机关和部门下达的最新文件及当前社会对于该话题的最新论点，借鉴多种要素分析法、听取了多位专家的意见和建议，最终从政治思想文化、政治管理制度、政治行政行为、政治生态反馈四个方面构建了政治生态综合评价指标体系，该体系包含三个层级，第一层级包含4 个指标、第二层级包含14 个指标、第三层级包含34 个指标。指标体系如图1 所示。

根据已建立的指标体系，可容易构建出其层次结构模型。层次模型中的第一层为目标层，即评价体系的总体方向；第二层为准则层，即评价政治生态的主要内容和影响因素，本体系中主要的影响因素为政治思想文化、政治管理制度、政治行政行为、政治生态反馈四大方面；第三层为子准则层、第四层为指标层，均是对上层指标的分解。综上所述，构建的层次结构模型如下表1 所示。

表1 政治生态评价指标体系层次模型

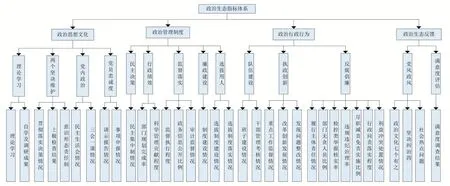
图1 政治生态综合评价指标体系

2.2 指标权重确定

2.2.1 构造成对判断矩阵

评价指标体系层次结构模型建立后，需对模型中具有向下隶属关系的元素分别构造成对判断矩阵A=（aij）mm，矩阵以该元素为判断准则，隶属其下的各子元素为比较对象，两两对比相对重要程度aij（其中：aij>0，aij=1/aji，aii=1）。相对重要程度参照表如表 2。

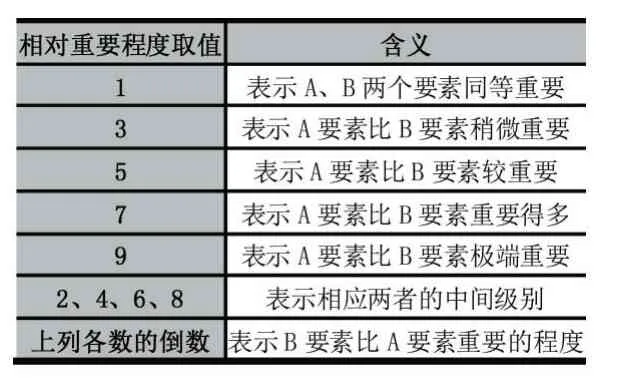
表2 相对重要程度参照表

由于判断矩阵A=（aij）m×m具有性质：aij>0，aij=1/aji，aii=1。aij>0 表示矩阵非负；aij=1/aji，aii=1 表示矩阵具有对称性；若矩阵满足aij*ajk=aik时，则矩阵具有传递性。而具备非负性、对称性、传递性的矩阵则为一致性矩阵，一致性矩阵或满足一致性允许范围内的矩阵能较好地保证各元素重要度之间的协调性，避免出现A 比B 重要，B 比 C 重要，而 C 比 A 重要的矛盾情况，而且在构建判断矩阵过程中，常采用群体决策的机制，邀请多位评判者构建各自的判断矩阵，最后通过加权平均法对评判者的评判结果进行融合。为了保证融合后的结果仍符合一致性，融合前须校验一致性，若不符合则需调整。构造成对判断矩阵的步骤为：

（1）构造成对判断矩阵 Ap（aij，k）m×m（p=1，2，…，f;k=1，2，...，s）（其中：f 为层次模型中具有向下隶属关系的元素个数，s 为参与评判的总人数）；

（2）将符合一致性的矩阵Ap（aij，k）m×m进行融合，构造最终的成对矩阵Ap=（aij）m×m。融合公式如下：

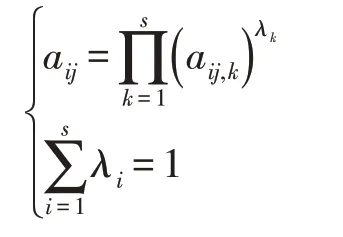
2.2.2 层次单排序及其一致性检验

矩阵构造完成后，接着需要进行层次单排序计算，并对矩阵做进一步的检验。计算步骤如下：

（1）利用MATLAB 计算各判断矩阵的最大特征值λmax 及特征向量 W=[ω1，ω2，...，ωm]T；

表3 随机一致性指标数值表

当CR 的值小于0.1 时，则该矩阵符合一致性，可将其计算出的经过归一化的特征向量作为单层指标权重，否则需调整相对重要值aij，重新构造矩阵。

2.2.3 层次总排序及其一致性检验

层次的单排序计算完成后便需要进行层次的总排序计算。层次总排序指的是体系中各指标相对于目标层的权重值，计算时通常由上层往下层依次计算而得。计算步骤如下：

（1）计算指标层层次总排序ωD=ωC×ωB×ωA；

（2）计算一致性比率CR1，检验一致性。

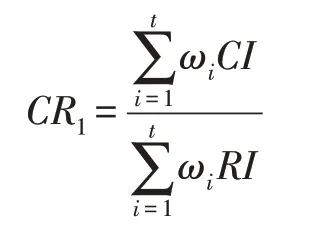
（其中：ωi 为指标权重，t 为指标层指标个数）

当CR<0.1 时，则总排序结果符合一致性要求，计算出的权重值可采用。

3 应用结果

指标构建过程中，我们邀请了5 位专家和10 位在党政机关工作多年具有丰富实践经验的领导干部，通过问卷的形式采集了各评判者的评判结果，然后采用上述方法计算指标权值，结果如图2 所示。经计算，评价体系的总CR 值为0.017，小于0.1，通过一致性检验。评价指标层次总排序如表4。

我们将构建的指标体系运用到了深圳市下属的64个单位中，并对2019 年各单位相关数据进行了监测和观察，统计分析结果如图2 所示。从图中可看出，得分在70-80 范围的单位数量最多，占比55%，而在60 分以下和90 分以上的比例较少，分别占3%和5%，统计结果与预估值较符合。因此，本文构建的指标体系在一定程度上较真实地反映了党政机关和部门的政治生态情况，能较科学地协助党政部门研判政治生态、净化化从政环境。

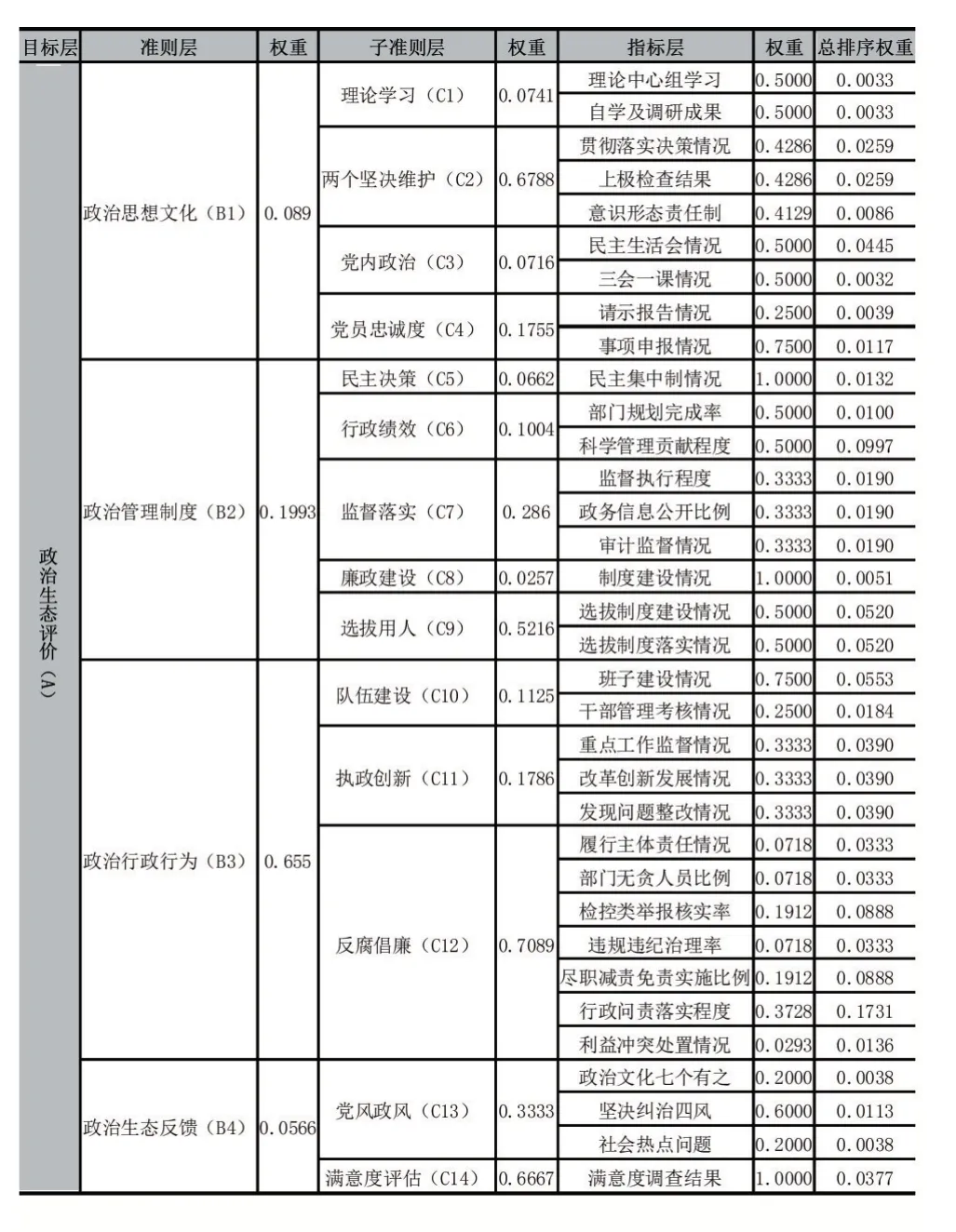
表4 指标模型层次总排序

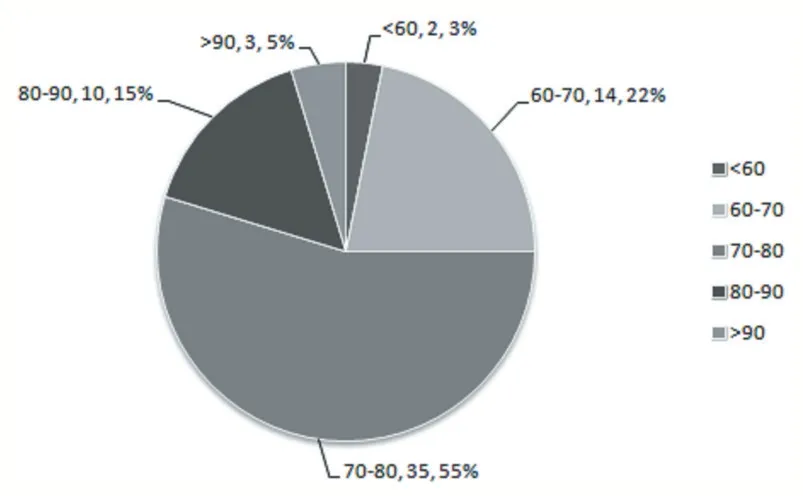
图2 政治生态研判结果分数占比

4 结语

本文结合党政机关最新的文件精神指引，从政治生态的内涵出发，依据我国政治生态研究的实际情况、分析党政机关从政环境的特征，采用了基于群组决策和层次分析两者结合的方法，构建政治生态评价指标体系，并为各指标赋予了相对重要程度权重。该方法的使用较好地将复杂问题做了层次分解，有效地将定性问题与定量问题相结合。经试验证明，该体系在一定程度上为党政部门研判政治生态提供了依据，同时，也为政治生态体系建设提供了新的参考。