导弹热发射燃气射流对发射筒的影响

邓春丽，袁 森,2*，张秀华

(1.贵州大学机械工程学院,贵阳 550025；2.贵州理工学院机械工程学院,贵阳 550003；3.贵州民族大学机械电子工程学院，贵阳 550025)

发射筒具有贮存、运输和发射导弹三种功用。目前大多数导弹都采用筒式发射，导弹尾喷管出筒前或出筒后的一段时间内，高温、高速、欠膨胀燃气射流排放在半封闭的发射筒体内部，此时，筒体不仅承受温度载荷，而且还承受压力冲击载荷[1]。温度载荷会使发射筒内的温度急剧升高，某些情况下会影响发射筒的安全性。而压力冲击载荷会引起发射筒筒体蒙皮和导弹尾翼损坏，从而影响导弹的发射。因此，需要对燃气射流的流动过程进行研究，从而为发射筒的结构设计提供理论指导。蔺翠郎等[2]采用动网格技术和流固耦合术对导弹发射过程中发射筒内的流场变化进行了研究，得到了筒壁的温度场，为发射筒的热强度设计提供参考，但是缺少发射筒在压力载荷作用下的研究。刘琦等[3]采用标准κ-ε模型，对贮运发射筒内燃气流产生的动力冲击波进行了研究，得到初始冲击波在发射筒内的流动过程。靖建全等[4]采用动网格技术对易碎盖前后端盖开启过程中发射箱内的流场变化情况进行了研究，得到了后盖开启后发射箱内不同区域平均压强变化情况，但是他们缺少发射筒在温度载荷作用下的研究。

为了研究导弹热发射过程中高温高压燃气流对发射筒的影响，采用动网格技术，建立发射筒和导弹的二维轴对称模型，模拟导弹发射过程中发射筒内的流场变化，进行筒内燃气流的温度、压强、速度分析；通过流场分析得到筒内的最大压力载荷和温度载荷，以这两种载荷作为发射筒瞬态动力学和瞬态热力学分析的边界条件，得出筒体的应力和变形，对今后发射筒的结构设计和优化提供理论依据。

1 理论基础

燃气流场模拟采用三维非定常Navier-Stokes方程组[5],湍流模型采用RNG(renormalization-group)κ-ε模型[6]，因该模型考虑了平均湍动能中的旋转及旋流流动，提高了数值模拟的精度，故选用此模型

质量守恒方程

(1)

动量守恒方程

(2)

能量守恒方程

(3)

对于边界运动的动网格，任意控制体V上的物理量φ的积分形式守恒方程[7]可写为

式(4)中:ρ为密度；u为流体速度；ug为运动网格的网格速度；Γ为扩散系数；Sφ为源项。

2 计算条件

2.1 计算模型

仿真模型模拟发射筒前后盖打开到导弹完全出筒的发射过程，导弹发动机点火到前后盖打开这一时间段燃气流对筒壁的作用时间短，故不考虑这段时间燃气流对筒壁的作用。首先对计算模型进行了简化，考虑计算资源和研究的目的，采用了二维轴对称模型，计算模型主要包括发射筒、喷管、导弹和外部流场，如图1所示。x、z、s为筒壁上设置的监测点。

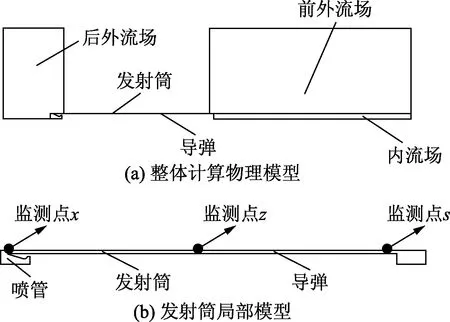
图1 仿真计算物理模型

模型网格划分如图2所示，在ICEM软件对模型进行区域分块，每一块区域均采用四边形网格，网格尺寸设置10 mm,网格总数为2.5×104。由于流场边界运动时，网格会发生变形，划分动区域时，应使网格的方向和流体流动的方向一致，避免出现负体积。

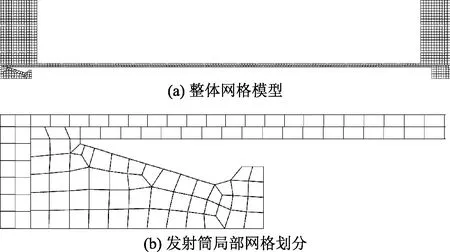
图2 计算网格模型

2.2 条件设定

将燃气按理想气体来处理，不考虑流体介质与固壁材料及环境的传热效应，不考虑燃气射流中的化学反应的影响及燃气中固体颗粒的影响[8]。燃气参数如表1所示。

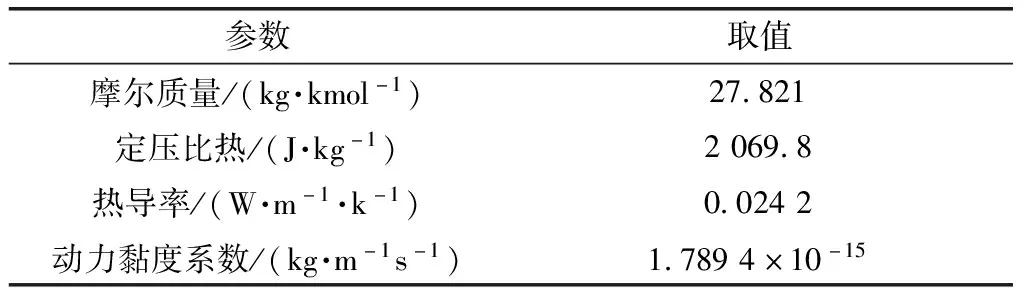
表1 燃气参数

计算边界条件设置压力进口、压力出口、壁面边界、轴对称[9]。压力进口的初始条件设置为压力随时间变化的，如图3所示。静压为0.23 MPa,燃烧室总温为3 000 K。压力出口边界条件压强为0.101 MPa,温度为300 K。发射筒的壁面、导弹弹壁、喷管外壁是绝热无滑移壁面边界。

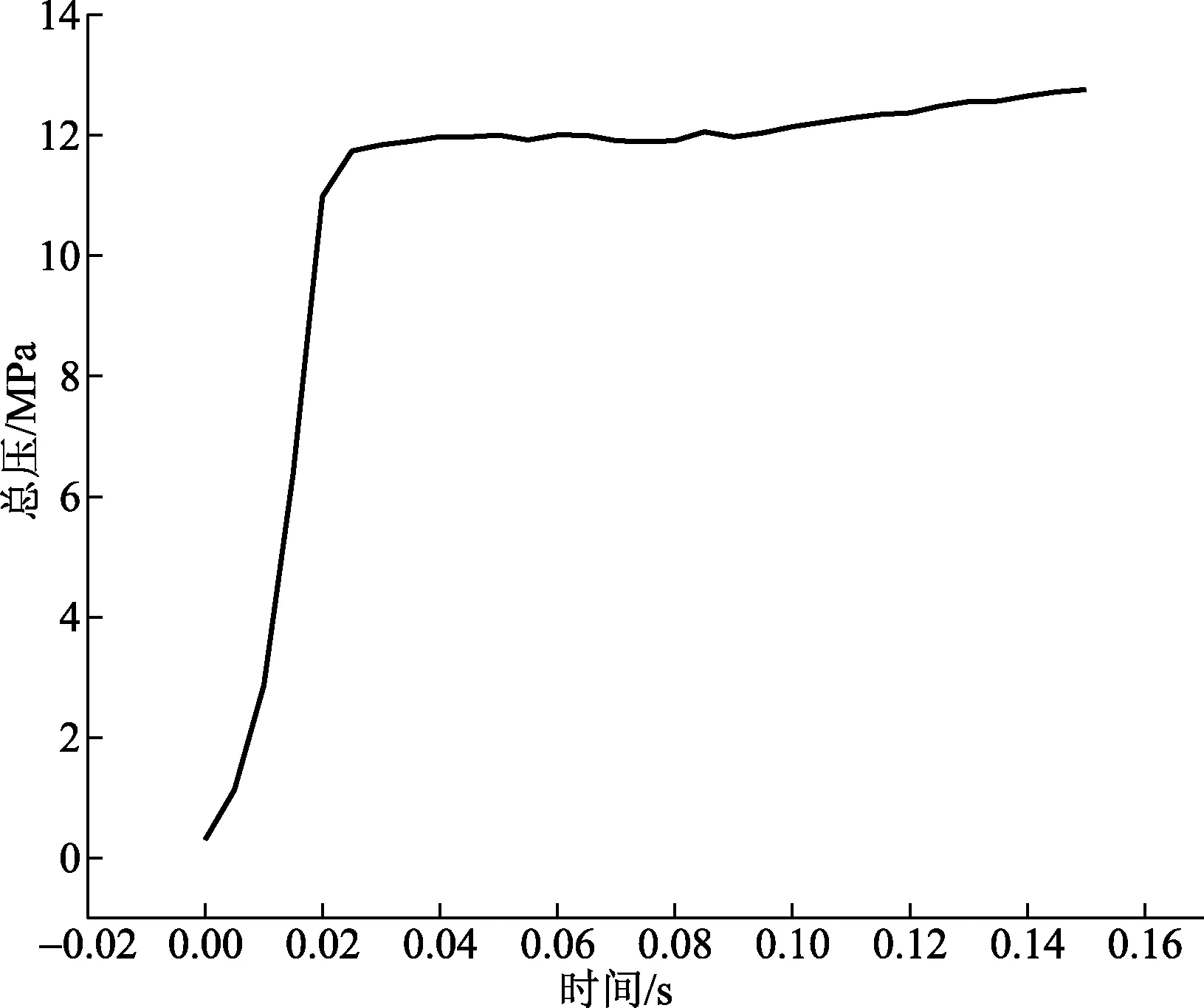
图3 总压变化曲线

计算中采用域动分层法进行网格更新。将计算区域分为内流场和外流场，内流场区域为运动区域，外流场区域为静止区域[10]。导弹发射时，将导弹运动速度赋给运动区域，运动区域前后边界静止，导弹附近的网格只运动不更新，运动区域的前后边界发生网格更新。如图4所示为导弹发射过程中计算域的网格变化图。

图4 发射过程中的网格变化示意图

2.3 计算方法

流场计算时，采用有限体积法对流场控制方程进行离散，使用压强隐式算子分裂(PISO)算法进行计算[11]。

根据筒内的流场变化，仿真中选取导弹发射初始、发射中段、发射末段三个时间段分析筒内的流场变化。

3 计算结果分析

3.1 仿真结果云图分析

图5为导弹发射初始时发射筒内燃气流仿真云图。由图5(a)、图5(b)可知，在发射初始时刻，喷管入口温度大约为2 980 K，因燃气流在拉瓦尔喷管出口处膨胀增速，使得筒内温度降低，大约为1 770 K。由图5(c)、图5(d)可知，导弹向上运动，燃气流从喷管出口向筒外扩散，由于发射筒前后盖都已打开，燃气流在筒内没有出现反射回流现象，且筒内的压强比喷管处的小很多。

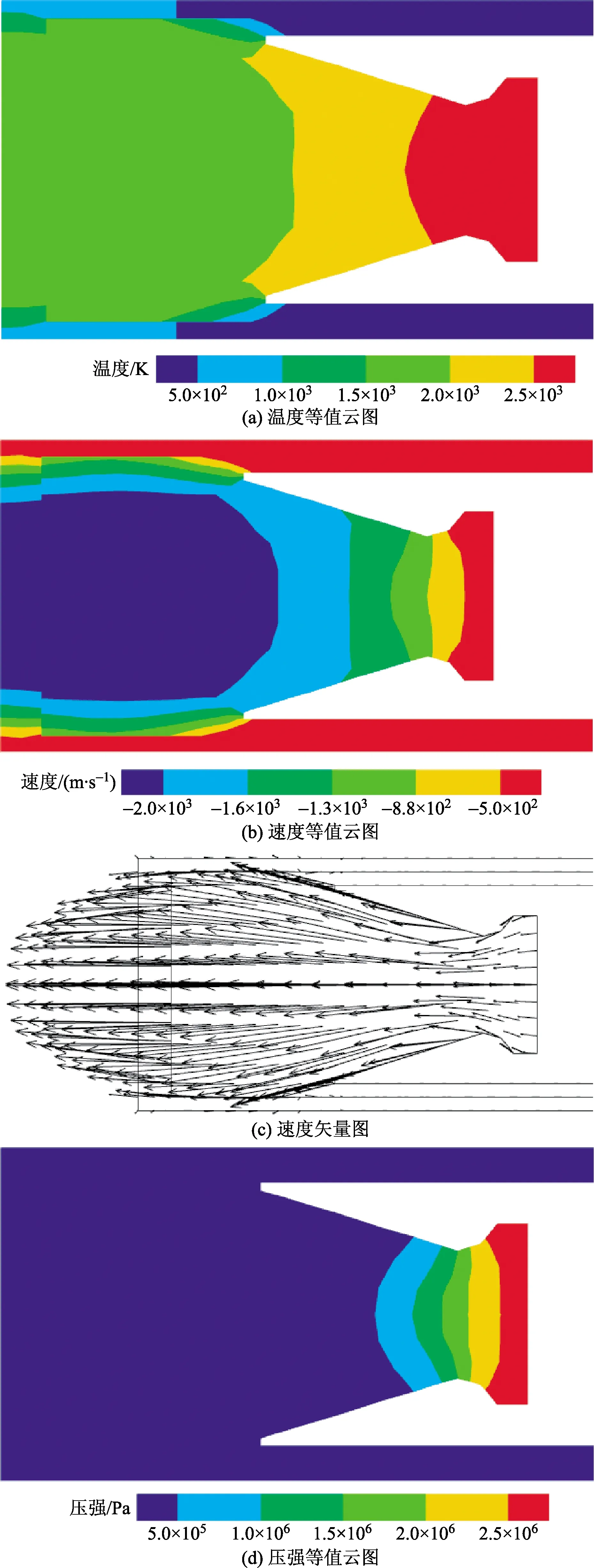
图5 发射初始段发射筒内燃气流云图

图6为发射中段时发射筒内燃气流仿真云图。由图6(a)、图6(b)可知，导弹发动机喷管已经运动到筒体的中部，筒内射流核心区的速度比筒壁上的大，故筒壁温度比筒内核心区的高,筒壁温度最大为2 180 K。由图6(c)、图6(d)可知，可以看出燃气流沿着筒底部的方向扩散，筒内燃气无反射回流现象。筒壁上的压强为513 191 Pa左右，只有喷管后方筒壁局部压强为1 101 040 Pa。此时壁面的压强会向外压迫筒壁，造成筒体向外变形。

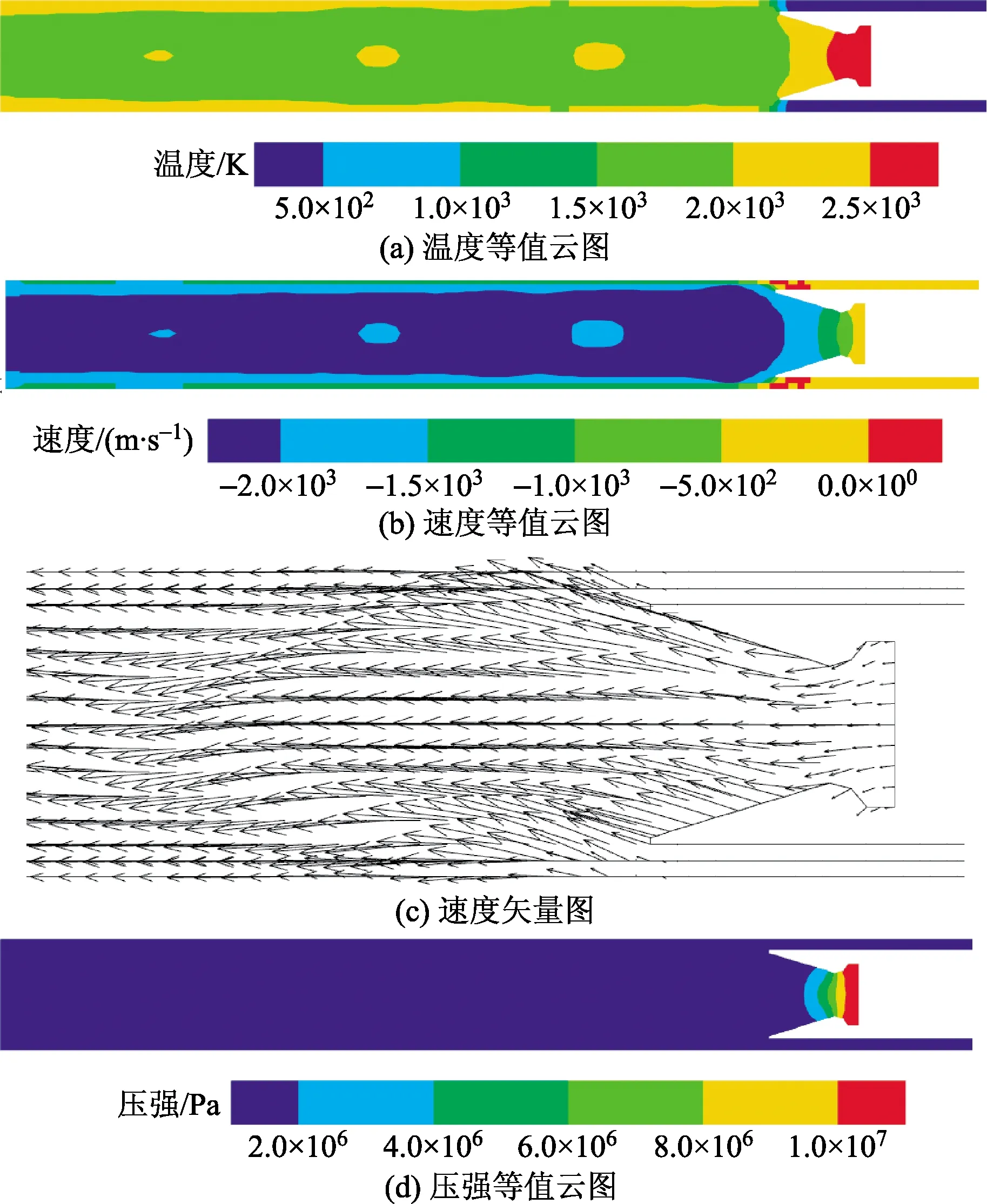
图6 发射中段时发射筒内燃气流云图

图7为发射末端时发射筒内燃气流仿真云图。由图7(a)、图7(b)可知，此时导弹已经完全出筒，筒壁下部和中部燃气速度比筒顶部的小，故筒壁底部和中部的温度要比筒壁上部要高，筒壁温度为2 172 K。由图7(c)、图7(d)可知，燃气流沿着筒底部的方向扩散，筒内燃气无回流现象，整个筒壁上的压强为1 119 479 Pa左右，此时壁面的压强向外压迫筒壁，造成筒体向外变形，由图8和图9得知，最大应力为83 712 000 Pa，最大变形为0.68 mm，筒体材料是铝合金，故发射筒的结构能满足使用要求。

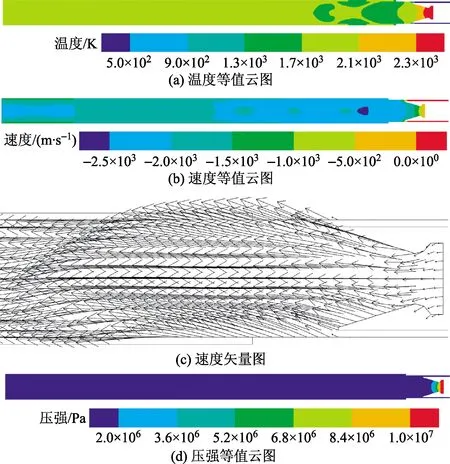
图7 发射末端时发射筒内燃气流云图

图8 发射筒应力云图

图9 发射筒变形云图

3.2 发射筒壁面监测点压强和温度变化分析

燃气流对筒体的影响以冲击和烧蚀为主，主要对筒体进行压强载荷和温度载荷分析。在发射筒壁上设置监测点，分析监测点的压强和温度变化趋势。图10为筒壁底部监测点x压强和温度变化曲线。由图10(a)可知，在发动机点火后，监测点x的压强最大为102 700 Pa，随后又产生一个100 750 Pa的负压，因为燃气流在筒内高速向后喷射，筒壁外侧向内压迫筒壁，导致筒壁向内变形，出现“内吸”现象，所以才会产生负压。随着导弹向上运动，冲击到筒底部燃气速度减少，导致该点的压强降低，之后又因为燃气流在筒内不断的增多，导致该点处的压强上升，最后趋于稳定。由图10(b)可知，发动机点火初期，筒壁底部监测点x的温度为300 K。0.02 s左右时，出现第一个峰值，温度从300 K变为303 K左右，表明发动机尾喷管尾部运动到该点，燃气流作用到该点，使得温度上升。随着导弹继续向前运动，越来越多的燃气流经此处，导致该点的温度继续增大。该点的温度虽增加，但是增幅较小，因发射筒前后端盖已打开，该点离筒口较近，筒内的燃气排导通畅，故该点的温度变化不显著。

图10 筒壁底部监测点x处燃气流作用分析

图11为筒壁中部z压强和温度变化曲线。由图11(a)可知，在发动机点火初期，该点压强上升到1 519 875 Pa左右。0.065 s时，发动机尾喷管尾部运动到该点，高压燃气作用于该点，使得该点处的压强上升。随着导弹向上运动，冲击到筒中部的燃气速度减小，导致该点的压强减小。由图11(b)可知，发动机点火初期，筒壁中部该点的温度为300 K。0.065 s时，出现第一个较大的峰值，温度瞬间从300 K变为2 257 K，发动机尾喷管尾部运动到该点，高温燃气作用于该点，使得该点处的温度上升。随着导弹继续往上运动，射流冲击位置逐渐远离此处，燃气对该点的影响作用变小，因此该点处的温度变小。又因为筒内一直有燃气流，故该点处的温度为2 000～2 250 K。

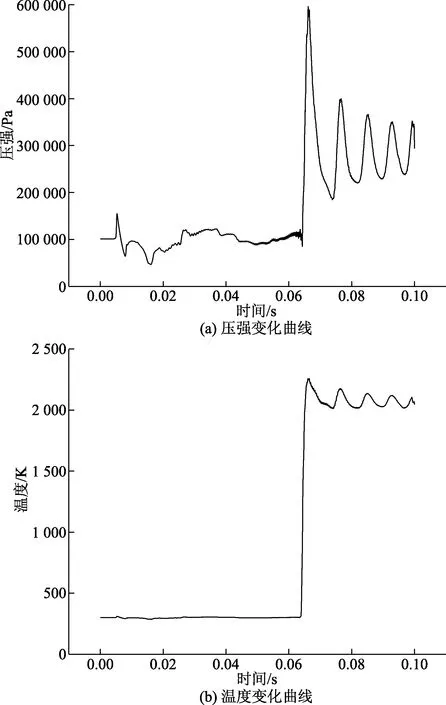
图11 筒壁中部z处燃气流作用分析

图12为筒壁顶部s压强和温度变化曲线。由图12(a)可知，在发动机点火初期，该点压强为101 325 Pa。0.1 s时发动机尾喷管尾部运动到该点，高压燃气作用于该点，使得该点处的压强上升到370 849.5 Pa。随着导弹向上运动，冲击到筒顶部的燃气速度减小，导致该点的压强减小。由图12(b)可知，发动机点火初期，筒壁顶部该点的温度为300 K。0.1 s时，发动机尾喷管尾部运动到该点，高压燃气作用于该点，使得该点处的温度瞬间从300 K变为2 250 K左右，随着导弹运动出筒，燃气流在筒口附近堆积，使得发射筒内的温度较高。

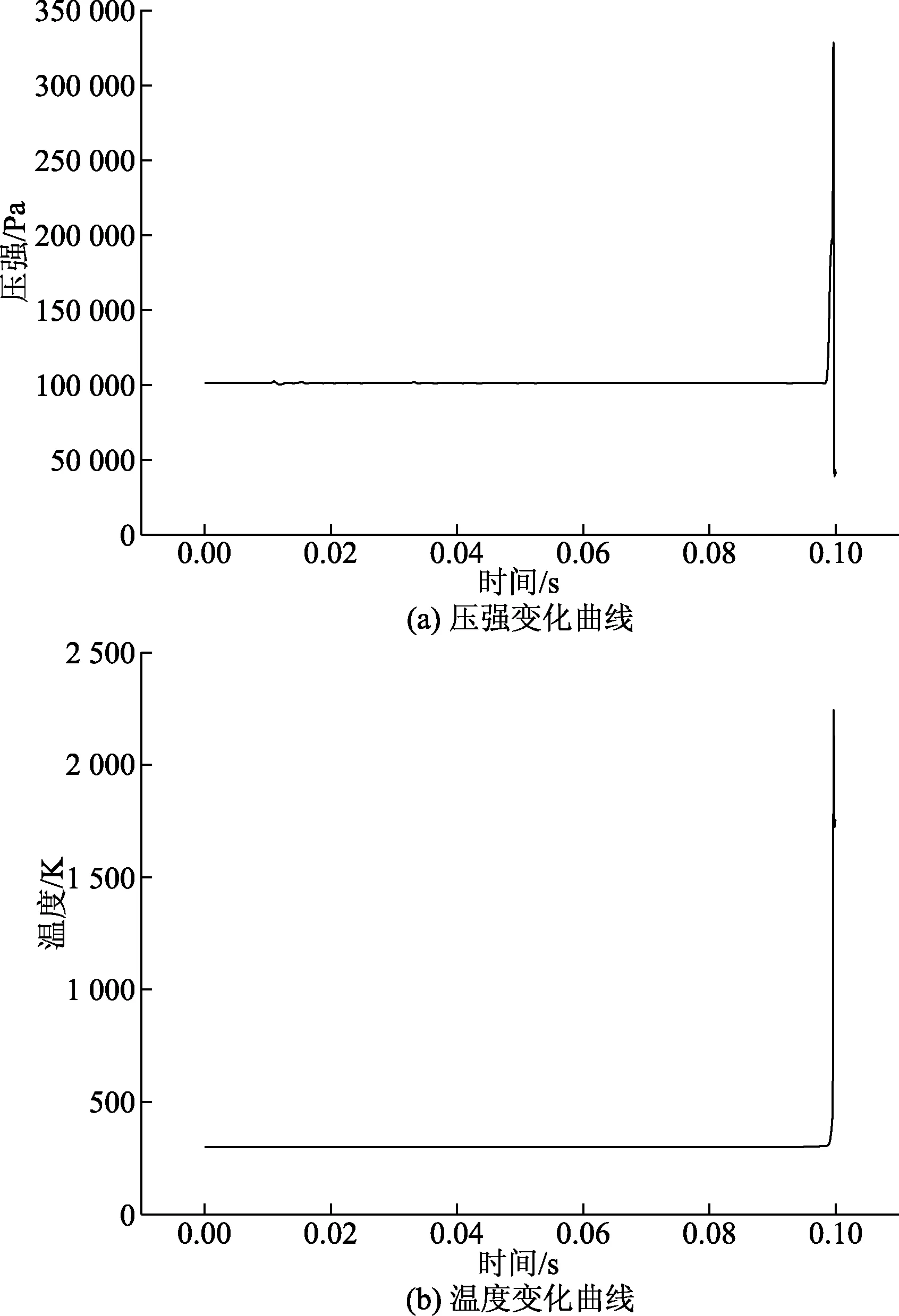
图12 筒壁顶部s处燃气流作用分析

从筒壁三个监测点的压强、温度变化曲线和筒体热应力和变形云图(图13、图14)可以得出，监测点z的最大温度为2 257 K,筒体在此温度载荷作用下，产生的最大热应力是1 271 800 Pa，热变形为0.1 mm，发射筒的结构满足使用要求。监测点z压强的峰值比其他两个监测点的大，最大为600 000 Pa。因发射初始时，燃烧室的推进剂燃烧不稳定，导致监测点x压强峰值变化次数比其他两个监测点频繁。发射中段时，因筒内空间小，燃气流排导不通顺，故监测点z和监测点s温度变化比监测点x温度变化大。

图13 发射筒热应力云图

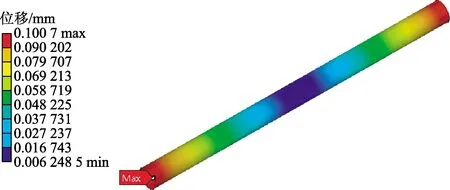
图14 发射筒热变形云图

4 结论

采用了域动分层动网格技术，模拟了前后端盖开启后到导弹发射出筒这一时间段燃气流对发射筒筒体的冲击效应，得出如下结论。

(1)导弹在发射初始段、发射中段、发射末端，筒内的燃气流都向筒外扩散，筒内无反射回流现象。

(2)导弹发射末段时，筒壁的压强值为1 119 479 Pa左右，筒体在此压强作用下，产生最大应力为83 712 000 Pa，最大变形为0.68 mm，满足使用要求。

(3)发射筒筒壁监测点z最大温度为2 257 K,在此温度下，筒体产生的最大热应力为1 271 800 Pa，最大热变形为0.1 mm，满足使用要求。

(4)发射筒壁监测点z的峰值比监测点x、s处大，监测点z和监测点s温度变化比监测点x温度变化大。