基于三角模糊熵-折衷排序法的终端区管制运行效率评估模型

闫少华，孙佳琦，张兆宁

(中国民航大学空中交通管理学院，天津 300300)

管制系统运行效率是管制单位最大限度的运用管制规则和系统资源，通过优化资源配置，使空中交通流处于快速、畅通、有序的程度，是反映管制系统运行状态的重要指标[1]。终端区管制系统是民航管制系统的重要组成部分，该系统中，空域资源有限，航路航线结构复杂，飞行状态复杂，这使得终端区成为空中交通运输网络的瓶颈。为了解决空域拥堵、航班延误的问题，需要客观科学地对终端区管制系统运行效率进行评估。

目前，中外学者已经逐步开展了空中交通管制系统运行效率的相关研究。在国外，美国交通运输部和联邦航空管理局，共同建立并完备了空中交通管制专家绩效评价数据库，为空中交通管理评价提供了有效工具[2]。EuroControl 2002在客观数据的基础上，从容量、效率、安全和环境影响四个方面评价空中交通管理系统的效率[3]。Viswanathan等[4]采用串联设计进行仿真建模，同时考虑层次结构，从战略、预战术以及战术三个层面研究管制运行效率。Bronsvoort等[5]提出了一种分阶段飞行效率的评估方法，构建了空中交通管理(air traffic management，ATM)性能与飞行效率的评估关系框架。

在中国，罗贯中等[6]以效率的内涵作为出发点，基于系统工程理论，从人-机-环三方面建立空管运行效率指标体系。张兆宁等[7]建立了基于数据包络分析(data envelopment analysis，DEA)的空域系统定量评估模型。杜实等[8]基于管制间隔运用现状建立了管制运行效率评估指标体系，利用含约束锥的DEA模型进行了管制运行效率评估。王梦丽等[9]利用DEA法中的两阶段BCC模型，对机场管制系统运行效率进行评估。林硕等[10]引入管制运行效率性指标，利用灰色关联逼近理想解法，对终端区管制系统运行质量进行定量评估。

综上所述，现有的管制运行效率相关研究通常是针对整个管制系统，专门针对终端区管制系统运行效率的研究相对缺乏,并且常用的主观赋权法多为基于1～9标度法的层次分析法，该方法构造一致性矩阵较困难，且所得出的结果与人的实际思维有较大差距。

首先根据终端区管制系统实际运行特点，构建适用于终端区管制系统运行效率评估的指标体系；其次选择能够更好反映专家真实判断的三角模糊数法确定主观权重，利用最小信息熵法将三角模糊数法求得的主观权重和熵权法求得的客观权重相结合，得到优化后的组合权重；最后运用折衷排序法(VIKOR)结合组合权重求出终端区管制系统运行效率评估值，并根据效率评估值进行排序，对终端区管制系统运行效率进行科学评价。

1 终端区管制系统运行效率评估指标体系建立

终端区管制系统是一个多元的输入输出系统，为其所辖空域的航空器提供空中交通管制服务。其基本运行过程为：根据现有的管制规则、终端区空域结构、天气状况以及航行情报等输入信息，通过利用通信导航监视设备、进程单填写来实施管制行为，输出进离场管制服务。因此，终端区管制系统运行效率是可以用管制系统提供管制服务能力来描述。

终端区管制系统的主要目标是保障终端区空域内的航空器快速、安全、有序的运行。因此，可以通过空中交流的快速、有序、安全的程度来反映终端管制系统管制服务能力，评价终端区管制系统运行效率。本文从终端区管制单位的运行实际出发，结合文献[11-13]充分考虑指标的典型性和可采集性，对终端区管制系统运行效率评价指标进行筛选、归纳和总结。终端区管制系统运行效率评价指标因素众多，将同类指标映射为同属性效率因子，每个属性对应管制运行过程中所关心的效率的一个方面。因此，从延误性、业务量、管制员工作负荷、终端区拥挤程度以及安全性五个方面构建终端区管制系统运行效率评价指标体系，如表1所示。

表1 终端区管制系统运行效率评价指标体系

各指标定义如下：

A1、A2、A3为由于航班延误的致因较多，在终端区运行效率评估时，只考虑由管制原因导致的进离场延误架次和延误时间。

A4、A5为由于离场航空器都按照标准仪表离场程序运行，管制员不需要过多进行调配，而进场航空器需要管制员不断地调整其速度、航向、高度来引导进场飞行，因此选择终端区进场效率来衡量终端区管制系统运行效率。终端区进场效率定义为：进场效率=1-额外进场时间/畅通进场时间，其中额外进场时间=总进场时间-畅通进场时间。

B1为经由终端区各边界点进出的小时流量。

B2、B3为B1中包含的起飞和着陆航班的小时流量。

C1为进近各扇区的管制员工作负荷。根据管制负荷直接测度法，假设管制员平均通话时间为t1，发布每条指令的思考时间t2=1.5 s，在工作时间段t内，共发出n条指令的工作负荷为：w=(nt1+nt2)/t×100%。

C2为指挥架次和通话总时长之比。

C3为通话总时长和值班时长之比。

D1、D2为航班的排队长度指等待排序的航空器架次。

D3为跑道的饱和度。已知跑道的实际容量Ccapacity，D1=B2+B3/Ccapacity。

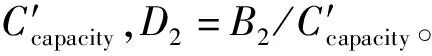
E1为根据自动化系统监视到的航空器4D航迹信息，实时监测航空器危险接近态势，得出终端区内航空器内的间隔冲突告警。冲突性指标监控航空器间隔标准，反映管制员的间隔情况，是反映运行效率的重要前提和依据。

2 终端区管制系统运行效率评估模型构建

基于三角模糊熵-VIKOR法的终端区管制系统运行效率评估，实质上就是综合运用三角模糊数法和熵权法求出主、客观权重，利用最小相对信息熵的原理得到组合权重，增大评估指标间的差异性，根据VIKOR法的原理，计算终端区管制系统运行效率指数值，对终端区管制系统运行效率进行量化评价。

2.1 指标打分及标准化处理

对不同指标进行标准化处理就为了是使不同指标具有可比性和一致性。“终端区航班小时流量”等指标为正向指标，指标指数值越大越优。“终端区进场因管制原因延误架次率”等指标为负向指标，指标指数越小越优。设Vij为第j个评估时段终端区管制系统内第i个评估指标值，n为待评估时段数量，一致性处理后的值为dij，正、负向指标的打分公式如下：

(1)

(2)

对所有指标进行标准化处理后，得到标准化矩阵D:

(3)

2.2 指标赋权

2.2.1 熵权法权重确定

根据熵权的定义，熵权值越大，该指标在效率评估中的作用越大；反之，熵权值越小，该指标在效率评估中的作用越小[14]。熵值法确定指标权重的方法如下：

(1)计算第i个指标，第j个评估时段的特征比重zij。

(4)

(2)根据熵值公式，计算第i个评估指标的熵值。

(5)

(3)假设评估指标的熵权集α=[α1,α2,…αm]T，第i个指标的熵值权重为

(6)

2.2.2 三角模糊法权重确定

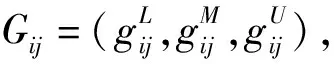
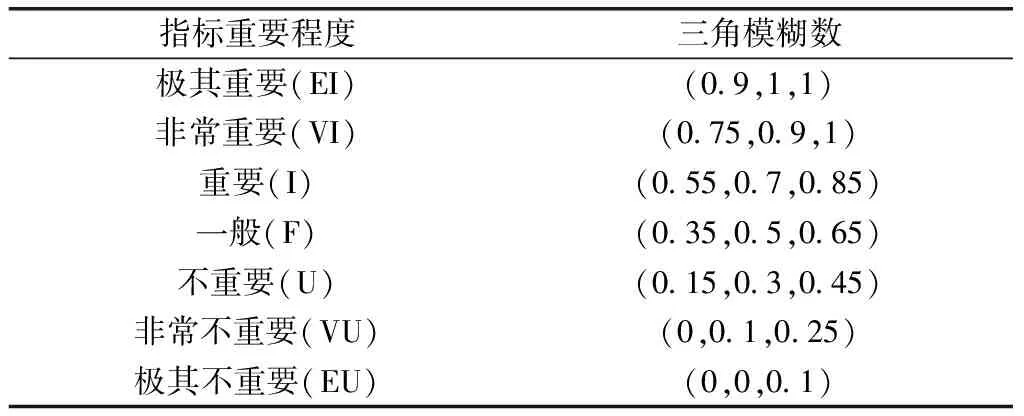
表2 指标重要程度及对应三角模糊数

(7)

(3)采用加权平均法对三角模糊数进行去模糊化，评估指标j的重要性精确评价值为

(8)

(4)设三角模糊权重集为β=[β1,β2,…,βm]T，将其归一化处理后得到第j个指标的模糊权重：

(9)

2.2.3 最小相对信息熵确定组合权重

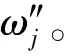
(10)

用拉格朗日乘子法求解式(10)得到组合权重wj：

(11)

式(11)利用几何平均数的方法，避免了在组合赋权过程中增加其他附加信息。

2.3 基于VIKOR的终端区管制系统运行效率评估模型

VIKOR是由Opricovic等基于折衷优化思想，并考虑正负理想解距离之间的相对重要性，提出的用于解决复杂系统多准则评价的方法[16]。终端区管制系统运行效率的评估是典型的多属性决策问题，因此，选择VIKOR法，构建终端区管制系统运行效率评估模型。

基于VIKOR法的终端区管制系统运行效率评估模型，具体步骤如下。

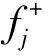
(12)

(13)

式中：Ωb是效益型指标集合；Ωc是成本类指标集合。效益型指标为A5、B1、B2、B3、C3，而包含A1、A2、A3在内的其余11个指标为成本型指标。

(2)计算各个评价对象的群体效用值Si和个体遗憾值Ri。

群体效益表示第i个方案到正理想解的加权距离，Si越小，代表群体效益越好，待评价的对象越优秀。

(14)

将第i个评价对象的最大遗憾值记为Ri，评价对象的个体遗憾值越小，评价对象越优。

(15)

式(15)中：ωj表示前文求得的第j个指标的权重。

(4)计算终端区管制运行效率折衷可行解Qi：

(16)

(5)计算终端区管制运行效率指数值。

折衷可行解Qi是待评价方案与理想解的距离，取值的范围在[0,1]之间，Qi值越小，效率越高。为了使评价值更符合生活实际，需对Qi逆向修正，本文定义终端区管制运行效率指数Ej，计算公式为

Ej=1-Qj

(17)

则可根据Ej大小进行排序，对不同时段终端区管制系统运行效率进行比较，Ej越大，管制效率越高。

3 实例分析

3.1 实例情况

选取中国某机场的终端区作为研究对象，采用双跑道隔离平行运行模式，该运行模式下，开设APP(S)和APP(N)两个雷达管制服务扇区。终端区边界设有5个进场点和4个出口点，其中，DOREX、MIKOS为进离场用点。以北京时间整点小时做时间段，选取该终端区某典型日8:00—22:00间的14 h段作为评价对象进行管制系统运行效率评估。

3.2 计算结果

根据三角模糊数法和熵权法求得主客观权重，然后利用最小相对信息熵法求得组合权重，结果如表3所示。

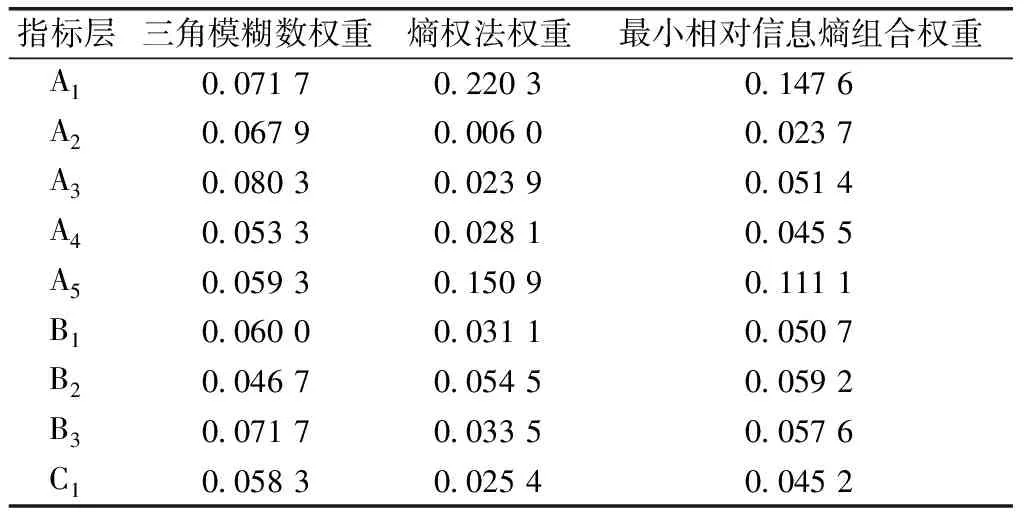
表3 评价指标标准权重

续表3

对原始数据进行标准化处理，结合指标的综合权重，计算14个时段的群体效益值Si和个体遗憾值Ri，取v=0.5，计算折衷可行解Qj，最后计算终端区管制运行效率指数Ej，并根据Ej值进行递减排序。评价结果如表4所示。

3.3 结果分析

由表4可知，VIKOR法和GRA-TOPSIS法所得到的同一时段终端区管制系统运行效率评价结果基本一致，排名位次差均不超过2，利用Spearman等级相关法，得到两种方法的相关系数为0.949(P<0.01)，该结果表明这两种评价法的关联度极高，说明两种方法所得评价结果具有较高的一致性，因此VIKOR评价法的计算结果是充分合理的。

此外，VIKOR法和GRA-TOPSIS两种方法所得的终端区管制系统运行效率综合评价值的极差分别为0.869 3和0.298 7，变异系数分别为0.486 0和0.170 9。极差越大，评价结果的分辨水平越强，离散程度越高。显然，VIKOR法的评价值极差和变异系数均大于GRA-TOPSIS法，因此，VIKOR法所得到的综合评价值相较于GRA-TOPSIS法，评价结果分布更加均匀合理，相邻排序间评价值差异更明显，更有利于直观区分各时段终端区管制系统运行效率水平，对终端区管制系统运行效率评价有较强的适宜性。

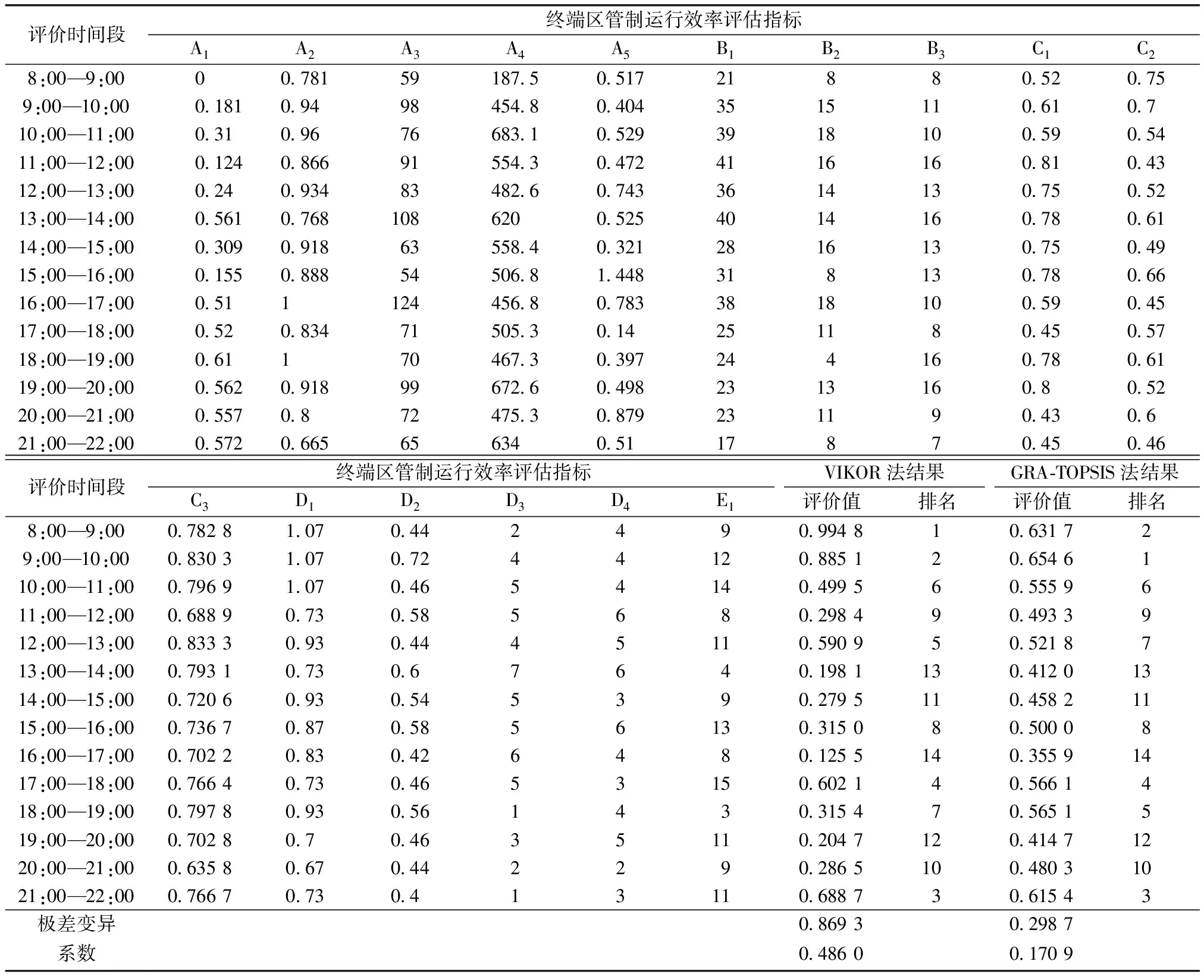
表4 某典型日某终端区8:00—22:00管制运行效率评估指标原始数据及评估结果

此外，在确定主观权重时，选择三角模糊数法。由图1可知，通过层次分析法(analytic hierarchy process，AHP)和三角模糊数得到的指标权重对比可知，三角模糊数确定主观权重时，通过语言变量对评价值进行模糊处理，更符合人的思维，得出的指标权重分布更平均，更加合理。

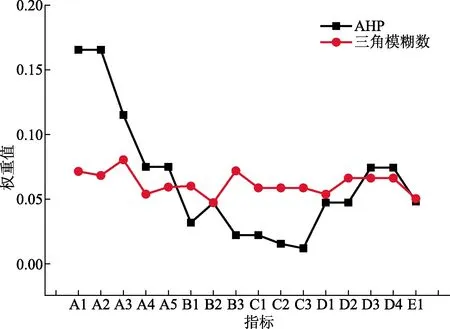
图1 层次分析和三角模糊数主观权重比较

由此可知，基于三角模糊熵-VIKOR法的终端区管制系统运行效率评估模型是合理且适宜的，根据当日终端区管制运行状况，综合评价得出如下结果。

(1)当日8:00—9:00、9:00—10:00这两个时段的终端区管制运行效率指数较小，管制运行效率较高。根据资深管制员经验，在这个时间段内，航班量较少，管制员工作负荷较低，由于早晨出港航班量较多，空中交通流较为稳定，空域利用率较高，不易出现飞行冲突，终端区管制系统整体运行效率较高，运行较为稳定。

(2)在13:00—14:00、16:00—17:00、19:00—20:00这三个时段运行效率最低。首先，这几个时段内航班量较大，终端区内交通流复杂，排队航班较多，跑道和终端区管制扇区始终处于饱和状态，导致飞行延误的发生，并且管制员工作负荷增加，不安全事件频发，管制系统运行效率较低，符合管制运行实际。

4 结论

从终端区管制系统实际运行过程出发，建立终端区管制系统运行效率评估指标体系；接着采用三角模糊数法得到评估指标的主观权重，利用熵权法得到客观权重，并利用最小相对信息熵法得出了组合权重。利用VIKOR法，计算出终端区管制系统运行效率指数值，对终端区管制系统运行效率进行量化评估。根据算例，得到如下结论。

(1)三角模糊数法确定主观权重时，克服了AHP法主观赋权时的主观臆断性，赋权过程更符合人的思维，得到的主观权重更加合理。利用最小相对信息熵法得出组合权重，最大限度地保留原始数据，同时使专家评分的客观性提高，指标权重量化结果更加合理。

(2)VIKOR法和GRA-TOPSIS法对同时段的终端区管制系统运行效率评估结果相关系数高达0.949，评价结果具有极高的一致性。但基于三角模糊熵-VIKOR法的率评估方法，评价结果分辨度更强，离散程度更高，评价结果更加均匀合理。且评价结果与管制运行实际结果相符，是有效可行的评估方法。

在对终端区管制系统运行效率准确评价之后，如何找出对终端区管制系统运行效率有重要影响的因素，并得出相应的效率提升策略，有待进一步研究。