航空螺旋桨振动特性的影响因素

魏武国

(中国民用航空飞行学院航空工程学院，德阳 618307)

航空螺旋桨是安装在航空活塞发动机、涡桨发动机上的推进器，给飞机提供拉力或者在飞机着陆时提供负拉力，文献[1]就从飞行试验角度给出了一种螺旋桨有效拉力的测量技术，而更多文献则侧重通过气动流场计算，分析螺旋桨自身性能或对机翼气动特性的影响[2-4]。

但为保证螺旋桨的工作可靠性并满足螺旋桨的适航性要求，还需对螺旋桨动力特性进行分析，要求其在工作转速范围内避免共振、避免出现桨叶颤振和整个桨盘的涡动颤振[5-6]。共振是桨叶在固有频率下，不断由激振源中吸取能量，以致桨叶结构的耗散能与供给能达到平衡，具有很大的振动应力，容易造成低周疲劳断裂[7]。为了保证螺旋桨合理避开共振工作点、在工作状态下的振动应力足够小并具有所要求的疲劳寿命，准确地了解和分析螺旋桨的固有频率和振型是最基础的工作[5-7]。

叶片的固有振动特性主要取决于刚度和质量分布以及安装方式，在实验研究方面：文献[6]采用试验模态技术研究了单个桨叶的振动特性，虽然分析了桨叶根部连接状态对固有频率和振型的影响，但没有研究离心、气动载荷对单个桨叶振动特性的影响；文献[7]仅通过扫频试验获得了桨叶静频，没有进行影响因素分析。在理论计算方面：文献[8-9]用有限元法分别对某型螺旋桨及其改型桨桨叶、某复材螺旋桨桨叶的振动特性进行了计算分析，两者都考查了桨叶在使用中是否会出现危险的共振，但在桨叶结构的动频计算中，都只考虑了离心载荷的影响，没有计及气动载荷。另外，文献[6-9]的分析或计算都只针对单个桨叶，没有研究螺旋桨整体的振动特性。

在分析航空螺旋桨结构特征的基础上，在通用有限元软件ANSYS中，建立了螺旋桨整体结构、以及单个桨叶结构的三维有限元模型。将螺旋桨在地面起飞状态下受到的气动、离心载荷进行组合，利用有限元软件计算了螺旋桨整体结构、单个桨叶结构在无外载荷下的、只有气动载荷作用的、只有离心载荷作用的、气动和离心载荷同时作用的自振频率和振型。通过对计算结果的分析，发现了气动载荷、离心载荷、形状(整体或单个桨叶)因素对频率、振型的影响规律，对其他与气体有相互作用的旋转部件的振动特性计算具有重要的指导意义。

1 螺旋桨振动特性有限元分析方法

1.1 模态分析基本理论

模态分析主要是为了计算结构的固有频率和振型，固有频率是在无阻尼状态下的自由振动频率，多自由度离散结构无阻尼自由振动的动力学方程为[10]

Mü+Ku=0

(1)

式(1)中：M为离散结构的质量矩阵；K为离散结构的刚度矩阵；u为离散结构的位移向量。

类似于螺旋桨结构的、与空气相互作用的旋转部件，除了要分析其在不旋转状态下的基本振动特性外，还需要分析其在常用工况下的振动特性，即分析其在有预应力(主要是离心、气动载荷引起的离心拉伸应力、弯曲应力和扭转应力)条件下的振动特性。当结构含有预应力时，式(1)就变为

Mü+(K+S)u=0

(2)

式(2)中：S为离散结构的微分刚度阵，由结构承受的预应力引起。其对结构模态的影响，还与结构的边界条件等有关，有可能会增加结构刚度，提高固有频率，也可能相反。

设离散结构各部位的振动为频率、相位均相同的简谐振动，即:

u=φsin(ωt)

(3)

将式(3)代入式(2)中可得：

-ω2Mφsin(ωt)+(K+S)φsin(ωt)=0

(4)

由于式(4)在何时均成立，故去掉含时间项：

(5)

式(5)中：ωj为第j阶固有频率；φj为j阶特征向量，模态形状因子。

式(5)中φj有非零解的条件是

(6)

求出ωj，再代入式(5)中进而可以得出振动特征向量φj。

1.2 ANSYS软件模态计算验证

利用ANSYS软件求解了根部固装悬臂梁(具体尺寸和材料常数见表1[11])固有频率的有限元解，并用理论解对有限元解进行对比验证。

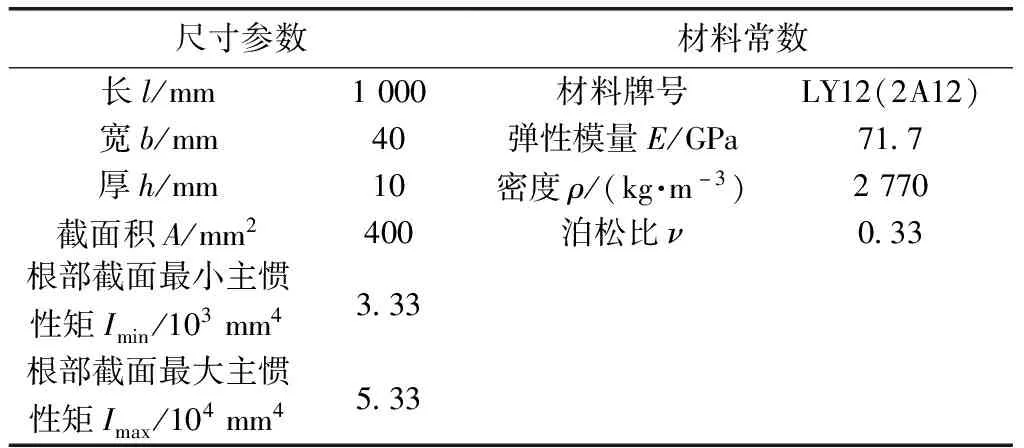
表1 根部固装悬臂梁的尺寸和材料常数

根部固装悬臂梁是一个类似于螺旋桨的狭长结构，提取其几何特征参数，建立三维几何模型和有限元模型，计算其固有频率，结果如表2所示。

弯曲振动固有频率f0i的理论计算公式[12]为

(7)

式(7)中：i为阶次，i=1,2,3，对应常数Qi=3.515、22.03、61.70。

从有限元解与理论解的对比可以看出，有限元解的最大误差为-1.93%，精度完全满足工程需要，因此可以用基于ANSYS软件平台的结构有限元模态分析方法计算螺旋桨的频率和振型。

表2 根部固装悬臂梁固有频率的有限元解与理论解

2 螺旋桨振动特性计算

2.1 分析对象及有限元建模

选取某航空活塞发动机的两桨叶定距螺旋桨为分析对象，基于通用有限元软件平台建立螺旋桨整体结构、单个桨叶结构的三维实体模型和有限元模型。

取螺旋桨材料为铝合金LY12(2A12)[13]，材料常数已在表1中列出。

网格划分时，桨毂部分采用Tet 10单元，桨毂上与桨叶结合的部位采用Pyr 13单元，桨叶前后缘采用Wed 15单元，桨叶叶身采用Hex 20单元。最后，螺旋桨整体结构共划得41 648个单元，122 528个节点；单个桨叶结构共划得20 824个单元，61 264个节点。

实际发动机上，螺旋桨桨毂与曲轴前端用精密螺栓紧配合连接在一起。相对于分析对象，可认为曲轴、发动机机匣等与其连接的结构刚度较大，当只分析螺旋桨整体结构或单个桨叶结构的振动时，可设定连接螺栓孔内的所有节点为固定约束。

由此建立起的三维有限元模型如图1、图2所示。

图1 螺旋桨整体结构的三维有限元模型

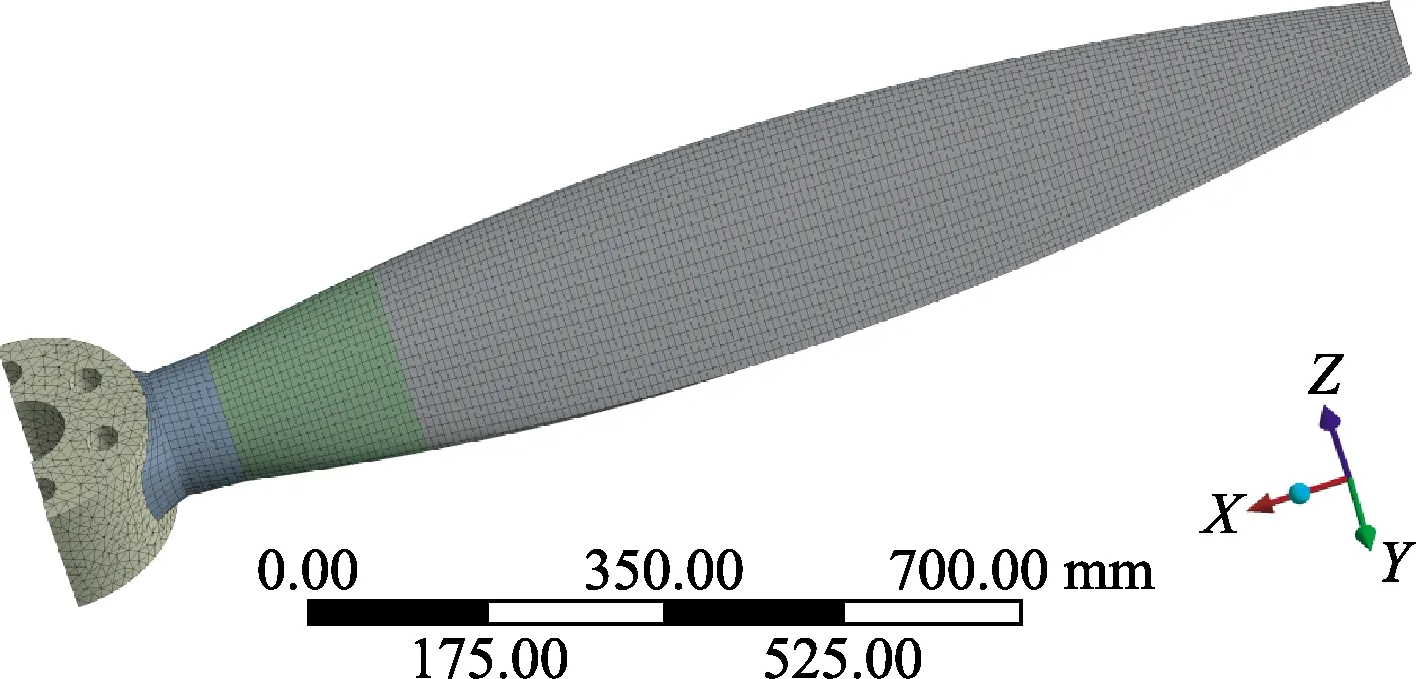
图2 螺旋桨单个桨叶的三维有限元模型

2.2 外载荷计算

航空螺旋桨是与空气相互作用的推进器，因此，要考察气动、离心载荷对螺旋桨振动特性的影响，就要选取螺旋桨的某个工况，将该工况下的气动、离心载荷作为螺旋桨模态分析的初始条件。

在不同的飞行阶段，飞机对航空活塞动力装置有不同的功率要求，螺旋桨承受的气动、离心载荷也会随着飞行阶段变化。螺旋桨在地面起飞状态时承受的气动、离心载荷最大，其对螺旋桨振动特性的影响也最大。因此选取该飞机在地面跑道的起飞工况，查询文献[14-15]，计算得到螺旋桨在该工况下的载荷如表3所示。

表3中，螺旋桨推进功率等于螺旋桨轴功率乘以螺旋桨效率，取螺旋桨效率为0.85。飞机在地面滑跑加速到28.30 m·s-1时抬前轮，地面起飞状态取5.14 m·s-1的滑跑速度。螺旋桨轴承受的扭矩是由螺旋桨旋转过程中、桨叶表面受到的切向气动阻力产生，螺旋桨拉力是由桨叶表面受到的轴向气动压力产生。考虑到桨叶旋转半径和表面面积，可将扭矩与拉力一起转换成桨叶表面均布的气体压力，与转速一起作为螺旋桨振动特性分析的外载荷。

表3 地面起飞工况下的螺旋桨载荷

2.3 振动特性计算过程

首先计算螺旋桨整体结构(或单个桨叶结构)的固有频率和振型。然后计算起飞工况下螺旋桨整体结构(或单个桨叶结构)承受气动、离心载荷的应力分布，此时的外载荷考虑三种情况：①只有气动载荷时；②只有离心载荷时；③真实情况，即气动、离心载荷都有时。最后将以上三种情况下的应力分布作为初始条件输入模态分析的有限元模型中，计算出螺旋桨整体结构(或单个桨叶结构)在气动载荷、离心载荷、真实情况下的自振频率和振型。

3 螺旋桨振动特性影响因素分析

3.1 预应力计算结果对比

不同载荷作用下的预应力计算结果如图3所示，此处只列出了螺旋桨整体结构的计算结果，单个桨叶结构的预应力计算结果与如图3所示的螺旋桨整体结构中的单片桨叶一致。

图3 螺旋桨整体结构在不同外载荷作用下的应力分布

由图3结合单个桨叶结构的预应力计算结果可以看出：只施加气动载荷时，螺旋桨上的等效应力最大值在①②③三种情况中最大，为200.21 MPa，位于距离旋转中心75%半径(该半径也是螺旋桨特征截面标定位置)的叶背处；只施加离心载荷时，螺旋桨上的等效应力最大值在①②③三种情况中最小，为76.05 MPa，位于桨毂与桨叶连接处；螺旋桨在真实的起飞工况下，等效应力最大值为 189.03 MPa，位于距离旋转中心75%半径的叶背处。

螺旋桨在真实起飞工况下的应力分布是气动载荷和离心载荷综合作用的结果，但此时的等效应力最大值反而由气动载荷单独作用时的200.21 MPa降低为了189.03 MPa，这主要是因为离心载荷增加了桨叶横向抗弯刚度，使承受气体压力产生弯曲变形的桨叶产生了恢复变形，应变减小，则应力减小。

另外，螺旋桨在真实起飞工况下的应力分布与气动载荷单独作用时的应力分布类似，且等效应力最大值接近、作用点位置相同。因此，可认为螺旋桨整体结构在真实起飞工况，由气动、离心载荷综合作用下的应力分布引起因素中，气动载荷占主导。

3.2 频率计算结果对比

螺旋桨整体结构的频率计算结果列于表4中，其中f0称为静频，把结构既不承受气动载荷也不承受离心载荷时(螺旋桨不工作时)的自振频率称为静频，即固有频率；把结构承受外载荷、含预应力时的自振频率统称为动频，仅承受气动载荷a时结构的频率用fd(a)表示，仅承受离心载荷a时结构的频率用fd(b)表示，同时承受气动和离心载荷c时(螺旋桨正常工作)结构的频率用fd(c)表示。

在螺旋桨整体结构自振频率的计算结果中，将不同载荷作用下的动频fd(x)[x=a,b,c]相对静频f0的增量作为纵坐标，振动阶次作为横坐标，画出曲线图4，结合表4可以看出以下结果。

(1)在仅有气动载荷作用时，螺旋桨弯曲各阶(1、2、3、4、6阶)动频相对静频增加不明显，频率增加不超过0.5%；扭转各阶(5阶)动频相对静频增加明显，增幅达到1.10%。

为进一步说明气动载荷对自振频率的影响，将气动载荷对静频的影响[即fd(a)相对f0的增量]和对动频的影响[即fd(c)相对fd(b)的增量)]作为纵坐标，振动阶次作为横坐标，画出曲线图5。可以看出，气动载荷对不管是静频还是动频的影响，与螺旋桨整体结构的振动形态有关，对桨叶弯曲自振频率影响较小，对桨叶扭转自振频率影响最大。

(2)在仅有离心载荷作用时，螺旋桨弯曲各阶(1、2、3、4、6阶)动频相对静频增加较明显，最大增量出现在1阶模态下，增幅达到23.31%；但随着阶次增加、振型复杂化，影响越来越小，6阶模态时，增量降为3.22%。扭转各阶(5阶)动频相对静频增加较小，增量仅为1.02%。

与气动载荷类似，离心载荷对自振频率的影响，也与螺旋桨整体结构的振动形态有关，对桨叶弯曲自振频率影响较大，但随着阶次增加，影响越来越小。对桨叶扭转自振频率影响较小。

(3)总体来看，气动载荷对自振频率的影响远小于离心载荷。

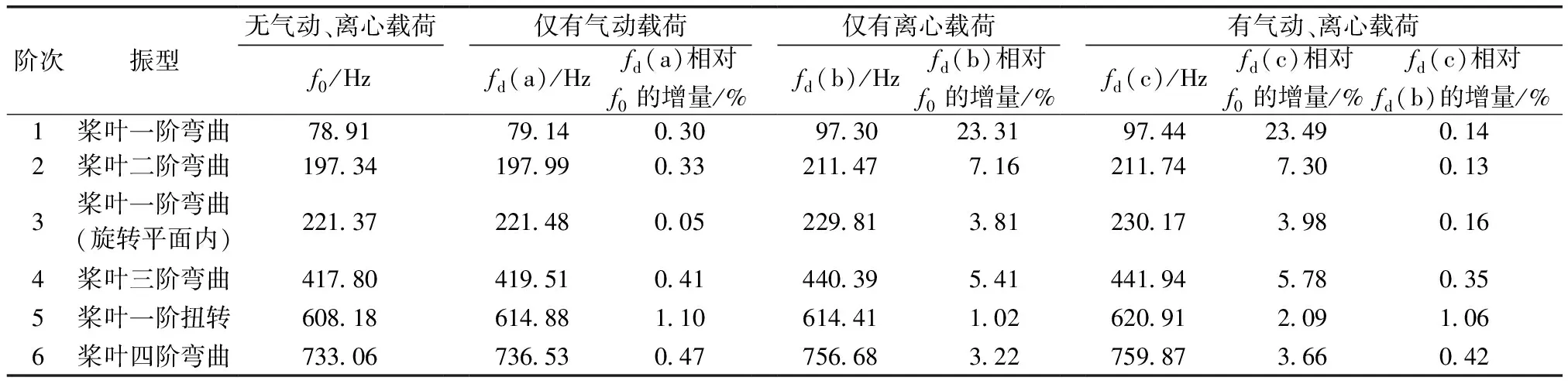
表4 螺旋桨整体结构在不同外载荷作用下的频率和振型计算结果

注：除特别说明外，螺旋桨整体结构的弯曲振型中，均在垂直于旋转平面的方向上振动。

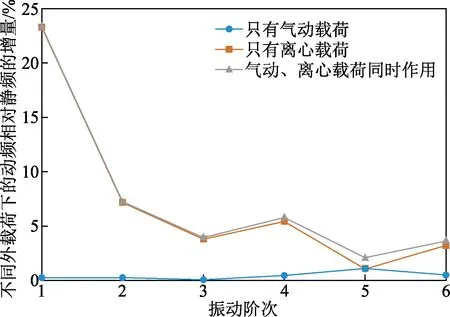
图4 外载荷对螺旋桨整体结构静频的影响

图5 气动载荷对静频和动频的影响

原因在于：离心载荷显著增加了桨叶的横向刚度，使式(6)中的微分刚度阵S变化，结构刚化效应明显，频率增加，特别是1阶模态。

但当气动载荷作用在桨叶表面时，改变更多的是桨叶起振的初始位移，而固有频率是结构的固有属性，与初始条件无关；气动载荷造成的结构预应力引起式(6)中的微分刚度阵S变化微小，因此频率变化微小。

在需计算类似螺旋桨结构、与气体有相互作用的旋转部件的振动特性时，可不计及气动载荷的影响，特别是在不便得到气动载荷的情况下或者是对结构动力特征初步设计时。

(4)气动和离心载荷同时作用在螺旋桨上，是该螺旋桨在起飞状态的真实受力情况，各阶动频相对静频的增量与仅施加离心载荷时的情况一致，1阶振动增量最大，5阶振动增量最小。结合(3)中的分析可认为，虽然在螺旋桨整体结构应力分布引起因素中，气动载荷占主导，但在外载荷对螺旋桨整体结构固有频率的影响中，离心载荷是主导因素。

为了找出形状因素对自振频率的影响，将螺旋桨整体结构和单个桨叶结构的静频、动频计算结果列于表5中，动频取在起飞状态下，气动、离心载荷同时作用时的频率。

定义静频的相对偏差Δ0/%为

(8)

同理，定义动频的相对偏差Δd/%为

(9)

从表5中看出，不管是静频的相对偏差、还是动频的相对偏差，都不超过0.05%，有些阶次下偏差为0。可认为，在同样的载荷条件下(无载荷或有载荷作用)，单个桨叶结构的同阶自振频率与螺旋桨整体结构一致，形状因素对自振频率无影响。在只需知道螺旋桨的自振频率时，可对单个桨叶结构建模计算，以节省计算资源、缩短计算时间。

3.3 振型计算结果对比

振型的计算结果列于表4、表5和图6～图8中。与单个桨叶的振动不同，两桨叶或多桨叶的螺旋桨，一个桨叶的动力特性会受到另一个桨叶质量-刚度-阻尼的影响，而明显呈现出耦合系统的动力特性。

螺旋桨整体结构的振动，在同一阶次频率下存在对称型模态和反对称型模态。对称型模态是指两片桨叶的振型相同、振动方向相同；反对称型模态是指两片桨叶的振型相同，但振动方向相反。但同一阶次频率下，螺旋桨整体结构的对称和反对称振型不能同时出现，而呈现出量子态特点。

表5 螺旋桨整体结构和单个桨叶结构的频率和振型计算结果

图6 螺旋桨整体结构前六阶固有对称振型

图7 螺旋桨整体结构前六阶固有反对称振型

图8 单个桨叶结构前六阶固有振型

如果是多桨叶螺旋桨，在同一阶次频率下，各桨叶的振型相同，但桨叶在振动方向上则存在正反组合。

另外，单个桨叶结构的振型计算结果反映不出螺旋桨整体结构的振动特性。

为分析外载荷对螺旋桨振型的影响，特选取不同载荷作用下螺旋桨整体结构1阶对称振型为例，如图9所示，桨尖处振幅是桨叶上的最大振幅：当仅施加气动载荷时，相对固有振型降低0.21%；仅施加离心载荷时，相对固有振型降低6.58%；真实情况下，气动、离心载荷同时作用时，相对固有振型降低6.71%，相对只有离心载荷时降低0.14%(气动载荷的影响)，相对只有气动载荷时降低6.51%(离心载荷的影响)。

图9 不同载荷作用下螺旋桨整体结构1阶对称振型

总体来说，外载荷作用下，螺旋桨整体结构的振型基本不变，但同一阶次桨叶上最大振幅相对固有振型(无外载)桨叶上最大振幅发生变化，如图10所示：1、2、5阶减小，3、4、6阶增大。另外还可看出，不管哪阶振型，桨叶上最大振幅的影响因素中，离心载荷占主导，气动载荷影响可忽略。桨叶上其他各点的振幅也有相同的变化规律。

单个桨叶结构也有类似结论。

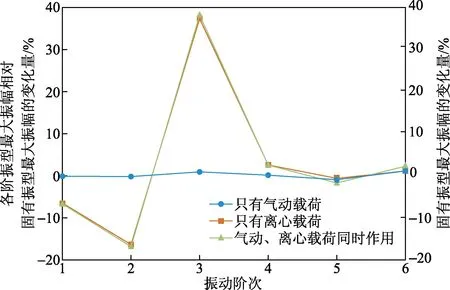
图10 不同载荷下桨叶上最大振幅相对固有振型的变化

4 结论

通过对螺旋桨整体结构、单个桨叶结构在不同外载荷作用下振动特性的计算，得到如下结论。

(1)螺旋桨结构静力特性的影响因素中，气动载荷占主导；振动特性(固有频率和振型)的影响因素中，离心载荷占主导。

气动载荷对桨叶扭转振动影响较大；离心载荷对桨叶弯曲振动影响较大，但随着阶次增加，影响幅度减小。总体上，气动载荷对结构振动特性的影响远小于离心载荷。因此，在其他与气体有相互作用的旋转部件振动特性的粗略计算中，可不考虑气体压力的影响。

(2)形状因素：螺旋桨整体结构的自振频率与单个桨叶结构同阶自振频率一致，因此可以计算单个桨叶的频率，来代替对整体结构自振频率的求解。特别是对于多桨叶的螺旋桨，可大大减小有限元模型求解规模，节省计算资源。

对振型的影响，螺旋桨整体结构的振型中，同一阶频率下存在对称和反对称振型，但不能同时出现，呈现量子态特点，单个桨叶结构的振型计算结果则不能反映这点。多桨叶螺旋桨整体结构的振型将更加复杂。