基于Polar码改进的抗量子密码方案
李 喆, 韩益亮, 李 鱼
(武警工程大学密码工程学院,西安 710086)
密码学在社会生活中的网上金融交易、国家民主选举、军队通信指挥等领域发挥着重要的作用。1994年,Shor[1]提出在多项式时间内解决基于大整数分解问题、基于离散对数问题的量子算法,RSA[2]、ECC[3]等密码受到潜在的危险。因此,许多学者寻找可以抵御量子计算机的新型密码体制,即抗量子计算密码体制(post-quantum cryptography)[4]。美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)面向世界征求抗量子密码方案,在候选的密码体制中,大约3/8的密码体制都是基于编码的密码体制[5]。26种候选的密码方案进入第二轮评选,进入第二轮评选的密码方案大多都是基于编码和基于格的[6],由此可见,基于编码的密码体制将是未来抗量子密码方案的研究重点。
McEliece等[7]首次提出基于编码的密码方案,该方案使用Goppa码作为原始编码,到目前仍然是安全的,但密钥尺寸较大。Niederreiter[8]提出基于GRS码的Niederreiter密码体制,该体制相较于McEliece体制,密钥尺寸有所减小,但距离实用化还有较大的差距。因此,许多密码学者寻求其他结构更为紧凑的编码以改进McEliece体制,通过换码改进的方案减小了密钥长度,但存在安全漏洞,容易受到信息集译码等攻击[9]。于是,又有学者对McEliece体制进行变形,如Kim等[10]构造了McEliece和Niederreiter相结合的McNie密码方案,刘相信等[11]构造了隐藏明文的汉明重量的密码方案。Esmaeili[12]采用汉明重量大于编码最小距离的错误向量,构造了一种满足IND-CPA安全性的密码方案。
Mostafa Esmaeili方案[12]没有采用置换矩阵和可逆矩阵对生成矩阵进行扰乱,且采用汉明重量大于编码最小距离的错误向量,可以抵御目前已知的信息集译码攻击,这种方法与McEliece有着完全不同的区别,为设计基于编码的抗量子方案提供了一种新的方向。该方案给出了理论框架,并未说明采用何种编码构造密码方案。在Mostafa Esmaeili方案[12]的基础上,根据Polar码在信道中的极化性质,采用Polar码作为改进方案选用的编码,把信息比特作为原方案中的明文,把冻结比特作为原方案中的随机比特串,密钥尺寸相较于McEliece方案减少70%。在译码过程中直接将冻结比特丢弃,并且改进Polar码的译码算法,提高了译码正确率。经过分析,该方案没有改变Mostafa Esmaeili方案的结构,仍然采用汉明重量大于编码最小距离的错误向量,可以抵御信息集译码等攻击。
1 基础知识
Polar码是目前为止唯一可以在理论上证明无限接近于香农限的编码。土耳其Arikan[13]提出Polar码后,近年来成为研究的热点,越来越多的学者开始研究Polar码的结构及性能[14-15]。Polar码信道极化现象主要包括信道联合和信道分裂两部分。通过信道联合和信道分裂后,各个子信道的对称容量将呈现两极分化的趋势:随着码长N的增加,出现信道容量趋近于1的无噪信道和信道容量趋近于0的全噪信道,信道容量趋近于1的无噪信道用来传输信息比特,信道容量趋近于0的全噪信道用来传输固定比特(冻结比特)。
1.1 相关定义
定义1一个二进制输入离散无记忆信道(binary input discrete memoryless channel,B-DMC)可以表示为W:X→Y,X是输入符号集合,Y是输出符号集合,,转移概率为W(y|x),x∈X,y∈Y。对信道W的N次极化后的信道可以表示为WN,则信道WN:XN→YN的转移概率为
(1)
对于一个B-DMC,有两个重要的信道容量参数。
(1)对称容量
(2)
(2)巴氏参数
(3)
式中:I(W)是对信道速率的度量;Z(W)是对信道可靠性的度量。信道W在等概率输入情况下,可靠传输时的最大速率为I(W);而信道W在只传输0或1的情况下,最大似然判决错误概率的上限为Z(W)。
I(W)与Z(W)的取值范围均为[0,1]。由于对数以2为底,因此码率和信道容量的单位为bit。I(W)与Z(W)满足这样的关系:当且仅当Z(W)≈0时,I(W)≈1;当且仅当Z(W)≈1时,I(W)≈0。
定义2信道极化。
信道极化分为两个阶段:信道联合阶段和信道分裂阶段。
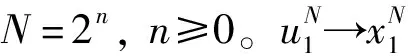
信道WN和WN的转移概率有如下关系:
(4)
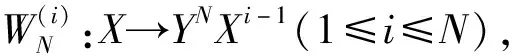
(5)
定义3信道极化定理。

定义4极化码编码原理。
极化编码步骤如下。
(1)极化信道可靠性估计:
(6)


(7)

BN=RN(I2⊗BN/2)
(8)
式(8)中:I2为2维单位矩阵,B2=I2;RN为置换矩阵,用来分离输入序列中的奇序元素和偶序元素,即先对奇序元素排列,再对偶序元素排列,例如:
(u1,u2,u3,u4,…,uN)RN=
(u1,u3,u5,uN-1,u2,u4,u6,uN)
(9)
1.2 Mostafa Esmaeili方案
Mostafa Esmaeili方案是Mostafa Esmaeili2019年在其博士论文中提出的,该方案的主要创新点是在McEliece加密方案的基础上,对McEliece方案的结构进行变形,利用汉明重量大于编码最小距离的错误向量的思想构造的密码方案[12]。该密码方案与McEliece方案构造过程类似,但是没有利用可逆矩阵和置换矩阵对生成矩阵进行扰乱,主要包括密钥生成(公钥、私钥),加密过程,解密过程三个部分。
1.2.1 密钥生成
G:域F上的维度为k、最小距离d≥2t+1的码C的kn阶生成矩阵。
H:域F上的(n-k)×n阶的校验矩阵。
S:(n-k)×(n-k)随机非奇异可逆矩阵。
公钥:[G,S(H-1)T],私钥:HTS-1。
1.2.2 加密过程
发送者选择长度为m的明文m,随机选择长度为r的随机比特串r(n=m+r),将随机比特串r与明文m并联,得到[r|m]。随机选择n-k位的向量s,计算sS(H-1)T,假如wt[sS(H-1)T] 发送者使用接收者的公钥对并联后的消息进行加密,得到: c=[r|m]G+sS(H-1)T (10) 1.2.3 解密过程 接收者收到密文c后,使用自己的私钥对密文进行解密。 cHTS-1={[r|m]G+sS(H-1)T}HTS-1=s (11) 接收者通过自己的私钥对密文进行解密得到s,然后用向量s乘以公钥S(H-1)T,得到sS(H-1)T,然后计算: [r|m]G=c+sS(H-1)T (12) 利用译码算法对[r|m]G进行解密,得到[r|m],把长度为r的随机比特串r丢弃,最后得到明文m。 首先定义对数似然比(log-likelihood ratio,LLR): (13) 因此,进行SC译码时,对于冻结比特可以直接对其进行判决: (14) 即当i∈AC时,表明该比特为冻结比特,即收发方事先约定好的比特,直接对冻结比特估计值赋值i∈AC。而当i∈A,表明该比特是信息比特,判决函数为 (15) i为奇数时: (16) i为偶数时: (17) SC译码算法步骤如下。 (18) (19) (3)进行判决: (20) (21) 返回(2)进行下一比特的译码,直到该码字全部译码完毕。 本文方案在Mostafa Esmaeili方案的基础上,并不改变原方案的形式,主要利用Polar码的极化性质,经过信道极化后,Polar码极化为有用的信息比特和无用的冻结比特,把信息比特作为明文,把冻结比特作为随机比特串,在译码过程中,直接将冻结比特丢弃,并对SC译码算法进行改进。本文方案主要包括密钥生成(公钥、私钥),加密过程,解密过程三个部分。 G:域F上的维度为k、最小距离d≥2t+1的Polar码C的k×n阶生成矩阵。 H:域F上的(n-k)×n阶的校验矩阵。 S:(n-k)×(n-k)随机非奇异可逆矩阵。 公钥pk=[G,S(H-1)T],私钥sk=HTS-1。 根据Polar码的极化性质,发送者将极化后的信息比特uA作为明文m,冻结比特uAC作为随机比特串r,将冻结比特uAC与信息比特uA并列,得到[uAC|uA]。随机选择n-k位的向量s,计算sS(H-1)T,假如汉明重量的值wt[sS(H-1)T] c=[uAC|uA]G+sS(H-1)T (22) 接收者收到密文c后,使用自己的私钥对密文进行解密: cHTS-1=([uAC|uA]G+sS(H-1)T)HTS-1=s (23) 接收者通过自己的私钥对密文进行解密得到s,然后用向量s乘以公钥S(H-1)T,得到sS(H-1)T,然后计算: [uAC|uA]G=c+sS(H-1)T (24) 利用改进的SC译码算法对[uAC|uA]G进行解密,得到[uAC|uA],把长度为r的随机比特串uAC丢弃,最后得到明文uA。 改进的译码算法步骤如下。 基于编码的密码方案的攻击,主要有密钥恢复攻击[17]和信息集译码攻击[18]两种类型的攻击。密钥恢复攻击的思想是通过公钥直接恢复私钥。信息集译码攻击通过密文恢复明文。 密钥恢复攻击是通过公钥恢复出私钥,即从S(H-1)T恢复出私钥HTS-1。 S(H-1)THTS-1=In-k (25) 攻击者找到私钥的概率为2k(n-k)。参数n和k在合理的选择范围下,本文方案可以抵御密钥恢复攻击。2018年,Drǎgoi等[19]针对基于Polar码的McEliece方案采用平方码技术进行密钥恢复攻击,本文方案中生成矩阵G是公开的,并没有像McEliece密码方案中采用可逆矩阵S和置换矩阵P对生成矩阵G进行隐藏,并不存在文献[19]攻击的情况,所以Drǎgoi等[19]提出的针对基于Polar码的密钥恢复攻击对本方案是无效的。 译码攻击通过寻找加密明文时的错误向量从而对密码方案进行攻击。译码攻击需要的工作因子小于密钥恢复攻击,所以通常情况下,攻击者采用译码攻击比采用密钥恢复攻击更有效。当错误向量的汉明重量小于编码的最小距离,攻击者采取译码攻击才有效,通过随机向量s乘以公钥S(H-1)T作为错误向量,假如错误向量sS(H-1)T的汉明重量小于编码的最小距离,则重新选择随机向量s,这样保证了采用的错误向量sS(H-1)T的汉明重量大于编码的最小距离,目前已知的译码攻击都是基于错误向量的汉明重量小于编码最小距离的情况,所以本文选择的错误向量,译码攻击是无效的。 信息集译码攻击一般是通过在接收端给定编码中的扩展集搜索最小重量的编码来寻找密文中的错误向量。信息集译码攻击采用MMT译码算法[20],所需要的工作因子为 (26) 信息集译码攻击试图找到与明文对应的k个无错误的密文位,即随机错误向量可以用纠错方法消除。本文所采用的错误向量的汉明重量大于编码的最小距离,所以通过纠错的方法不能消除本文方案中的错误向量。目前为止,信息集译码算法都是在错误向量的汉明重量小于编码最小距离的情况下攻击的,还没有已知有效的攻击算法在错误向量的汉明重量大于编码最小距离情况下找到k个无误差位。因此,本文方案可以抵抗信息集译码攻击。 计算复杂度主要包括两个部分:加密复杂度CEnc和解密复杂度CDec。 4.1.1 加密过程 c=[uAC|uA]G+sS(H-1)T 加密的复杂性主要取决于矩阵乘法和错误向量。 所以加密复杂度: CEnc=Cmul([uAC|uA]G)+Cadd[sS(H-1)T] (27) Cmul([uAC|uA]G)=O(k×n) (28) Cadd[sS(H-1)T]=O[(n-k)×n] (29) CEnc=Cmul([uAC|uA]G)+Cadd[sS(H-1)T]≈ O(k×n) (30) 4.1.2 解密过程 (1)所采用的延迟译码算法,对于每个节点都采取延时判决,采用后一节点的判决结果来代替当前节点的判决,提高当前节点正确判决的概率。 (2)假设第一个信息比特之前有L1个冻结比特,后面有L2个冻结比特,即L1+L2=n-k。改进后的延时判决译码算法,需要计算的节点数L=4k+L1+2L2-1,算法复杂度为O[2nlgn-(n-1)]。 (3)改进后的延时译码算法复杂度虽然比原来的SC译码算法略有提高,但是相较于原来的译码算法,译码正确率大大提高。 cHTS-1=([uAC|uA]G+sS(H-1)T)HTS-1= s[uAC|uA]G=c+sS(H-1)T[uAC|uA]= Dc[c+sS(H-1)T] (31) 解密的复杂性主要取决于译码算法和cHTS-1: 所以解密复杂度 CDec=Cmul(cHTS-1)+CSC[c+sS(H-1)T](32) Cmul(cHTS-1)=O[n(n-k)] (33) CSC([uAC|uA]G)=CSC[c+sS(H-1)T]= O[2nlgn-(n-1)] (34) CDec=Cmul(cHTS-1)+CSC([uAC|uA]G)≈ O[n(n-k)] (35) 本文方案的公钥为[G,S(H-1)T],私钥为HTS-1。 公钥量: Mpk=kn+(n-k)n=n2 (36) 私钥量: Msk=n(n-k) (37) 密钥量: M=Mpk+Msk= kn+(n-k)n+n(n-k)=n(2n-k) (38) McEliece方案的公钥为Gpub(其中Gpub=SGP),私钥为(S,G,P)。 公钥量: (39) 私钥量: (40) 密钥量: (41) 将本文方案与McEliece方案进行对比: (1)将本文方案的公钥量与McEliece方案的公钥量比值定义为 (42) (2)将本文方案的私钥量与McEliece方案的私钥量比值定义为 (43) (3)将本文方案的密钥量与McEliece方案的密钥量比值定义为 (44) 本文方案与McEliece方案进行对比如下。 (1)公钥量:根据表1,当本文方案和McEliece方案都选用Polar码,本文方案的公钥尺寸比McEliece方案略大;根据表3,当本文方案采用Polar码,McEliece方案采用Goppa码,本文方案的公钥尺寸约是McEliece方案的2倍。 (2)私钥量:根据表1,当本文方案和McEliece方案都选用Polar码时,本文方案的私钥尺寸减小为McEliece方案的4%;根据表2,当本文方案和McEliece方案选用码率越高的Polar码,减小私钥尺寸效果越明显;根据表3,当本文方案采用Polar码时,McEliece方案采用Goppa码时,本文方案的私钥尺寸减少为McEliece方案的5.7%。 (3)密钥量:根据表1,当本文方案和McEliece方案都选用Polar码时,本文方案的密钥尺寸减少为McEliece方案的30%;根据表2,当本文方案和McEliece方案选用Polar码时,码率越高,减小密钥尺寸效果越明显,选参数为(1 024,921)时,密钥尺寸减少约70%,当R≈1时,理论上,可以减少约75%;根据表3,当本文方案采用Polar码,McEliece方案采用Goppa码,本文方案的密钥尺寸减少为McEliece方案的48%。 方案的公钥量比McEliece方案的公钥量略大,但私钥量远远小于McEliece方案的私钥量,重要的是,本文方案整体的密钥量(公钥量,私钥量)远小于McEliece方案的密钥量。 本文选用参数为(1 024,921)的Polar码,密钥量与McEliece方案相比,减少约70%。 表1 基于Polar码的本文方案与McEliece方案对比 表2 基于Polar码的本文方案与McEliece方案在不同参数的对比 表3 基于Polar码的本文方案与基于Goppa码的McEliece对比 证明了选用码率高的Polar码,将有效减小密钥存储空间;方案中采用了汉明重量大于编码最小距离的错误向量,使其能抵抗信息集译码攻击。下一步可以寻找威胁本方案安全性的其他类型的攻击。 Mostafa Esmaeili的方案目前只是对消息进行加密,在将来的工作中,可以尝试在数字签名,密 钥交换,密钥封装等方面进一步研究,将方案的新思想应用于其他密码学原语。 在Mostafa Esmaeili方案基础上,利用Polar码的极化性质和Mostafa Esmaeili方案的特殊结构,提出了基于Polar码的抗量子密码方案,并改进了译码算法,提高了译码正确率。在合理的参数选择下,该方案私钥尺寸和整体的密钥尺寸相较于McEliece方案大大减小,整体的密钥尺寸减少了约70%,促进了密码方案的实用化。本方案没有改变Mostafa Esmaeili方案的结构,依然采用汉明重量大于编码最小距离的错误向量,可以抵抗目前存在的信息集译码等攻击,达到IND-CPA安全。选用的Polar码正是华为5G控制信道技术使用的编码,利用Polar码构造密码方案,将是未来5G时代研究的热点。1.3 SC(successive cancellation)译码算法
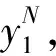
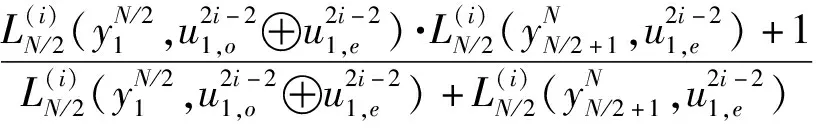
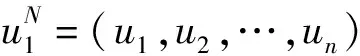

2 基于Polar码改进的抗量子密码方案
2.1 密钥生成
2.2 加密过程
2.3 解密过程


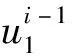

3 安全性分析
3.1 密钥恢复攻击
3.2 译码攻击
3.3 信息集译码攻击
4 性能分析
4.1 复杂度分析
4.2 密钥尺寸分析



5 结论

