基于时间序列分解与全连接神经网络的警情长周期时间序列预测

石少冲, 陈 鹏,2*, 曾昭龙, 胡校成

(1.中国人民公安大学信息技术与网络安全学院，北京 102600；2.安全防范技术与风险评估公安部重点实验室，北京 102600；3.社会安全风险感知与防控大数据应用国家工程实验室，北京 100043)

对犯罪活动进行态势感知、情报挖掘、分析研判和预测是公安机关进行犯罪打击和预防的重要工作。其中，犯罪预测由于对勤务资源的调度和指挥具有重要的参考价值，受到了各级公安部门的高度关注。目前，在犯罪预测的研究领域，研究人员主要采用各类时间序列预测方法对犯罪活动的时间趋势进行预测分析。从总体来看，现有的犯罪时间序列预测工作大体可以分为两个方面，一是使用单一模型进行犯罪时间序列的预测，比如Yadav等利用ARMA模型预测了犯罪距离[1]，Rodriguez等利用时间序列方法对旧金山犯罪数量进行了预测[2]，申贵成等[3]利用时间序列预测了短期交通流量，陈鹏等[4]则利用孤立点挖掘发现了警情时间序列的异常点，单勇等[5]采用X-11方法对温州市龙湾区的盗窃犯罪数量进行了预测，陈鹏等[6]使用ARIMA模型对廊坊市的110警情数据进行了短期预测，张立强等[7]利用一阶整值对盗窃犯罪时间序列进行了预测，陈鹏等[8]使用模糊粒化支持向量机对警情时间序列进行了预测，等等；二是使用复合模型进行犯罪时间序列的预测分析，比如陈鹏等[9]构建了灰色-马尔可夫模型对廊坊侵财类警情数量进行了预测；涂小萌等[10]提出了ARIMA-LSSVM模型对犯罪时间序列进行了预测；刘美霖等[11]构建了ANN-STARM模型预测了警情的数量，等等，从实际应用来看，其效果要好于采用单一模型的预测精度。然而，这些研究大都以预测短期内单位时间的案发数量为目标，同时由于犯罪事件本身随机性强，且容易受到人为因素和突发因素等多重噪声因素的影响，因此实现犯罪或警情时间序列的精准预测往往十分困难，即便能够达到较好的预测精度，也只能实现短期内预测，无法实现长周期的预测。实际上，从当前公安工作的需求来看，其对犯罪或警情的时序预测不再以精准的数量预测为主，而是希望获得未来一段时期内警情的分布或风险级别以便于提前进行勤务资源的机动调度和部署。为此，针对警情时间序列的特点，以时间序列和神经网络模型为基础，提出了一种适合警情时间序列长周期预测的STL-FNN模型，并以实际数据进行分析，通过与传统的预测方法相比较证明其在犯罪预测领域的有效性。

1 时间序列分解原理

对时间序列Yt，其可以分解成趋势项分量Tt、周期项分量St和残差项Rt，其表达式如式(1)所示：

Yt=Tt+St+Rt，t=1,2,…，N

(1)

解趋势项分量Tt、周期项分量St和残差项Rt可以通过以鲁棒局部加权回归作为平滑方法的时间序列分解方法(seasonal decomposition of time series by loess，STL)得到[12-13]，其分为内循环与外循环两个过程，其中内循环主要实现时间序列趋势分量的拟合与周期分量的计算，STL的外循环主要为调节鲁棒性权重，以减少残差项Rt的异常值对时间序列分解产生影响。

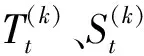
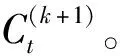
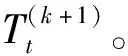
在内循环每次迭代过程中，在(2)与(6)做LOESS回归时，邻域权重需要乘以鲁棒性权重ρt，以减少异常值对内循环的影响，鲁棒性权重ρt计算为：对任一时刻t，时间序列Yt的鲁棒性权重ρt的计算如式(2)～式(4)所示:

(2)

(3)

h=6median(|Rt|)

(4)

式中:B为双平方函数；h为中间变量。

2 全连接神经网络

全连接神经网络(fully connected neural network，FNN)是一种非线性模型，是基于仿生人脑神经系统工作原理而演化而来，具备强大的非线性函数逼近能力[13]，其相应的演化模型应用十分广泛[14-16]。全连接神经网络是指任意相邻两层即n-1层任一神经元节点都与n层的所有神经元节点相连，第n层每个神经元节点在进行计算时，其激活函数的输入值是n-1层所有神经节点的加权。其中yi为第n层第i个神经元节点的输出值，f为第n层第i个神经元节点的激活函数，xj为n-1层第j个神经元节点的输出值，wj为对应的权重值。其公式如式(5)：

(5)

激活函数采用广泛应用的线性整流函数(rectified linear unit，ReLU)，公式如式(6)：

(6)

损失函数采用均方差(mean squared error，MSE)，公式如式(7)：

(7)

式(7)中：observed指真实值;predicted指预测值;N为预测值个数。

3 STL-FNN预测模型

从STL和FNN模型的算法原理可以看出，STL模型主要通过提取时间序列Yt中的趋势项分量Tt和周期项St，并以Tt为基础来进行短期趋势预测。而相比之下，FNN模型由于其强大的非线性拟合能力能够对时间序列Yt中的非线性分量，如周期项St和残差项Rt进行较为精准的预测。因此，根据警情时间序列预测的现实需求，提出一种基于STL和FNN模型的警情时间序列长周期预测模型。将警情时间序列的周期项分量St和残差项Rt记为组合项Mt，则警情时间序列可以表示为

Yt=Tt+Mt

(8)

基于STL-FNN警情时间序列长周期预测模型结构如图1所示，其实现步骤如下。

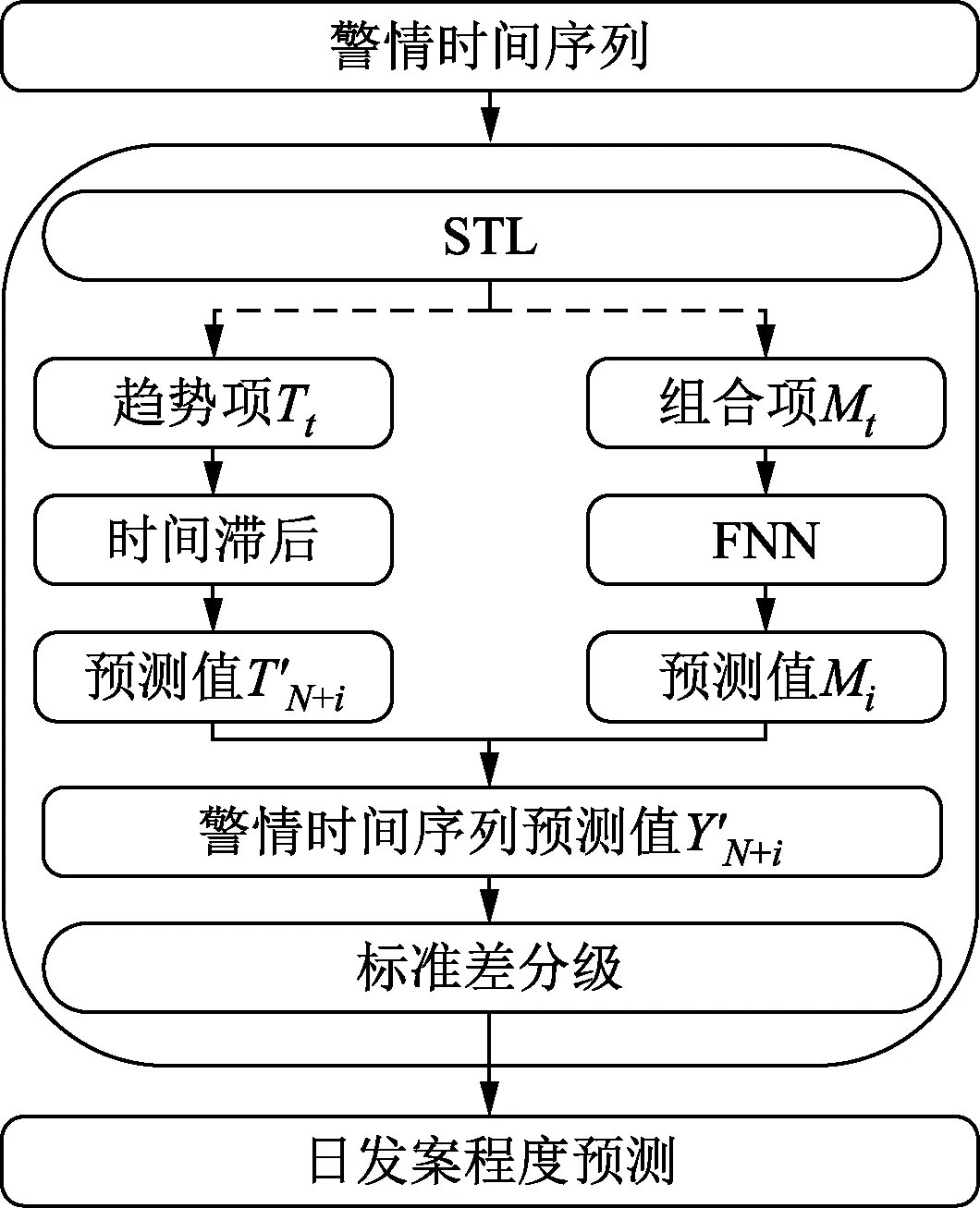
图1 STL-FNN预测模型组成

(1)将周期长度为k的警情时间序列训练数据Yt(t=1,2,…,N)导入模型，利用STL提取时间序列的趋势项Tt和组合项Mt，设提取到的时间序列趋势项序列为

Tt={T1,T2,…,TN}

(9)

设提取到的时间序列组合项为

Mt={M1,M2,…,MN}

(10)

(11)

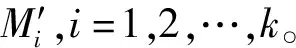
(12)

(4)对得到的预测结果进行相应的标准差分级，最终得到一个周期内的单日警情风险等级。

4 案例分析

4.1 数据来源

为验证STL-FNN预测模型的有效性，以B市的盗窃类犯罪时间序列数据为例进行一年周期的预测。数据的时间区间为2004—2014年，期间共发生盗窃类警情478 328起。以2004—2013年的数据作为训练数据，2014年的数据为验证数据。首先，对B市的盗窃类警情记录进行数据转化，生成时间序列，时间单位为1 d。在特殊年份的处理方面，2004年、2008年、2012年均为闰年，除二月以外，闰年的时间长度与平年相同，而闰年的二月份比平年的二月份仅多出2月29日1 d，其观测值样本较少，为减少平年、闰年的划分对研究工作的影响，更好地研究说明盗窃类案件的全年规律，需要将闰年特殊处理成平年，即删除2月29日的数据。其次，在处理缺失值方面，采用相同日期历史案发量的均值代替失时期的缺失值。

4.2 发案风险等级划分

在单日警情风险等级的划分上，采用标准差分级的方法[17-19]。根据公安部门的预测预警标准，采用四色分级方法，将警情数量转化为四类等级，分别标示为“轻度”“中度”“重度”和“严重”。具体划分方法如表1所示。

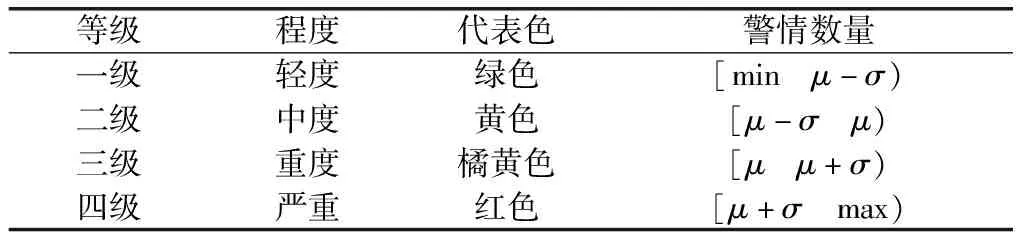
表1 警情日风险等级划分

注：min为实际警情最小值；μ为实际警情数量的均值；σ为实际案发数量的标准差；max为实际案发数量的最大值。如果预测的警情低于min，则将其划分为一级，若预测的警情高于max，则将其划分为四级。

4.3 性能评价

机器学习领域有一系列测试性度量方法来反映所训练模型的性能[20]，这些测试性度量方法主要通过混淆矩阵实现。对此，STL-FNN模型的测试指标借鉴了机器学习领域的混淆矩阵来衡量模型分级能力，混淆矩阵是一种观察统计真实类别和预测类别的交叉列表，如表2所示。

表2 混淆矩阵

在机器学习领域，类别i被称为兴趣类别，非类别i被称为非兴趣类别，i∈(轻度，中度，重度，严重)。其中，P(a)是指模型真实值一致性比例，Pr(e)表示期望一致性的比例，TP为真阳性(true positive),代表正确分类为感兴趣类别样本的数量；TN为真阴性(true negative),代表正确分类为非感兴趣类别样本的数量；FP为假阳性(false positive),代表错误分类为感兴趣类别样本的数量；FN为假阴性(false negative)代表错误分类为非感兴趣类样本的数量。评价指标主要采用Kappa值、预测精确度(Precision)、回溯精确度(Recall)和正确率(Accuracy)，公式如下：

(13)

(14)

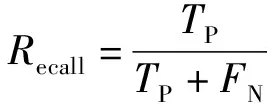
(15)

(16)

4.4 预测结果

以2004—2013年间B市实际盗窃警情时间序列数据为训练集，以2014年B市实际盗窃警情时间序列为测试集，利用STL-FNN模型进行预测分析。同时，为便于对比，同样采用Holt-Winters模型、LSTM模型、Prophet模型和ARIMA模型进行数据训练和预测。图2、图3分别为STL-FNN模型、Holt-Winters模型、LSTM模型、Prophet模型和ARIMA模型的预测结果及2014年B市盗窃类警情时间序列实际发案风险等级，其中构建的ARIMA模型为ARIMA(5,1,1)。

图2 各模型分级预测结果

从图2可得，STL-FNN模型对2014年B市盗窃类警情时间序列风险等级的预测效果与实际结果最为接近，其中模型对“轻度”“中度”“重度”和“严重”四种单日警情的风险分级预测较为准确，模型的延展性及可信度较高。而Holt-Winters模型则存在对“轻度”“中度”和“严重”风险等级预测不充分，对“重度”预测过度的问题。LSTM模型和Prophet模型仅能对“中度”“重度”风险等级进行有效预测，但两者的预测精确程度不高。ARIMA模型则失去了分级预测能力且对“中度”风险等级产生了学习过度现象。

4.5 预测结果评价

利用Kappa值、预测精确度、回溯精确度和正确率四个指标分别对不同的模型预测结果进行评价，评价结果如表3所示，其中Precision1、Precision2、Precision3、Precision4分别为对“轻度”、“中度”、“重度”和“严重”警情风险等级的预测精确度；Recall1、Recall2、Recall3、Recall4分别为对“轻度”、“中度”、“重度”和“严重”警情风险等级的回溯精确度。从表2中可见，STL-FNN模型的整体预测性能要好于其他四种模型。其中，STL-FNN模型对“轻度”“中度”“重度”和“严重”的警情风险分级预测能力较好，各项性能得分较为均衡，具有很好的稳健性；Holt-Winter模型对“重度”识别的可信度是各个模型中最好的。LSTM模型、Prophet模型和ARIMA模型则不具备预测“轻度”“中度”“重度”“严重”四级的能力。STL-FNN模型整体对四类警情日风险等级预测的准确率为62.47%，相对于其他四种传统模型有着更好的预测效果，并可正确预测一年内228 d的实际警情风险等级。

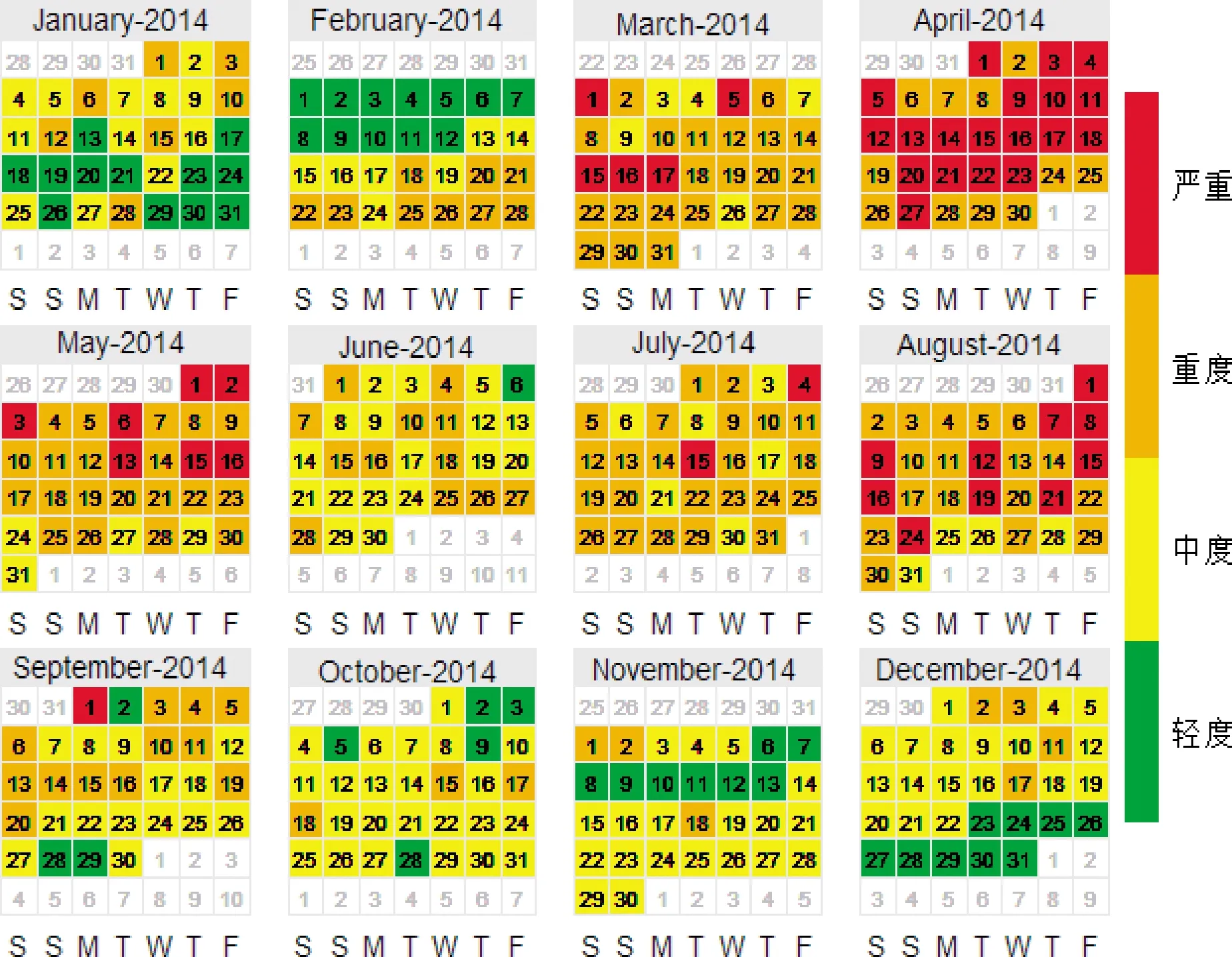
图3 实际警情的分级结果

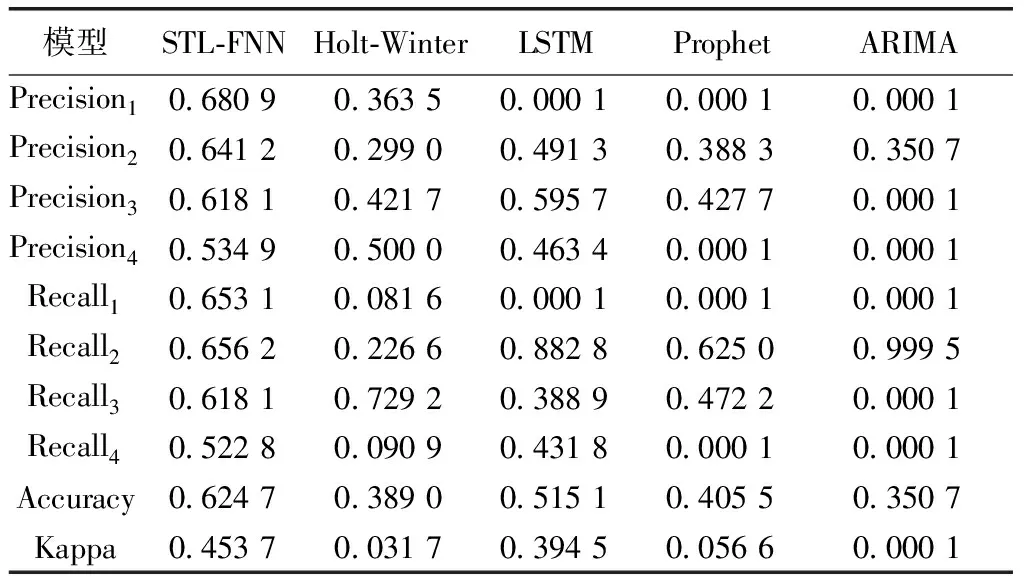
表3 各个模型分级预测的评价指标

5 结论

针对警情时间序列预测存在的不足，基于警情时间序列预测的实际需求，设计并提出了一种基于STL-FNN警情时间序列长周期预测模型。该模型能够综合STL和FNN算法的特点，实现对警情时间序列的长周期风险等级预测。通过实证分析表明，STL-FNN模型能够实现周期为一年的警情时序预测，并且预测效果要优于传统的预测模型。在实际应用上，STL-FNN模型可以帮助公安机关预测未来警情的长周期时间趋势，有助于预先发现警情异常的日期，辅助公安机关对犯罪活动的作案时间规律进行研判，从而制定有针对性地制定警务巡逻计划和打击犯罪计划。