基于改进的粒子群优化BP神经网络浙江电能替代潜力预测模型
李昌祖,牛东晓*,张欣岩,苗 博
(1.华北电力大学经济与管理学院,北京 102206;2.中国电力科学研究院,北京 100192)
环境污染、气候变化是人类共同面对的话题,而中国化石能源占终端能源消费的比例偏高,会造成严重污染和资源的浪费,电能相对其他能源具有明显的优势,为了实现经济社会的绿色、可持续发展,中国提出要大力推进电能替代发展战略,积极引导企业用清洁能源替代一次能源,提高电能在能源结构中的消费占比。
通过对未来区域电能替代电量预测,可以分析区域的电能替代潜力,可以对电能替代项目的替代电量工作认定进行规范化,有利于加快发展电能替代战略,实现能源发展方式转变,保证电能替代工作的科学性和规范性。因此,研究区域电能替代潜力的预测方法具有重要的现实意义。
目前,电力预测方法有很多,随着经济的发展和电力体制改革,电力需求的影响因素越来越复杂,对电力预测模型的精度要求的也越来越高,经典预测算法和传统预测方法已经无法满足当前的电力需求形势,正逐步被现代人工智能预测技术所替代。文献[1]基于电能替代环境负荷模型和脱钩理论,设定了多个电能替代发展情景,通过智能算法修正预测模型,实现了2020—2050 年不同情景下的电能替代潜力有效预测;文献[2]以地区GDP、人口数量和终端能源消费量为评价指标,对河北省各个地区的电能替代潜力进行了排名分析,然后基于灰色(GM)预测与神经网络组合预测模型实现了河北省电能替代潜力多情景预测;文献[3]基于山东四大能源终端消费结构和特点,构建了热当量求解模型预测电能替代潜力。文献[4]构建了数据包络分析(DEA)模型和灰色预测模型对中国农村电能替代潜力进行了短期和长期的分析,结果表明,中国农村电能替代潜力较大,电能使用比例在近期电能替代技术水平和用电规模条件下,能得到大幅度提高,从而减少碳排放,有效缓解能源紧缺的现状。文献[5]基于新疆地区历史全社会用电量数据,构建了多元线性回归和神经网络组合预测模型,预测了新疆地区未来5 a的全社会用电量;文献[6]利用岭回归方法分析了北京市终端电能替代量与人口、能源价格等因素的关系,并构建了可拓展的随机性的环境影响评估(STIRPAT)模型将各个因素进行了分解和量化,从而研究未来北京电能替代潜力。但是,在电能替代潜力预测研究中,研究者们主要关注的是经济因素、人口因素与电能替代电量之间的规律,并且预测精度并不能完全满足需求。而本文将考虑政策因素、环保因素和电能替代技术因素等对电能替代电量的影响,并用改进的灰色关联分析算法进行影响电能替代电量的关键指标筛选,将归一化后的数据代入到改进的粒子群优化神经网络(IPSO-BP)模型中,对浙江地区未来电能替代电量进行预测。
1 改进的GRA-IPSO-BP算法
1.1 灰色关联分析算法及改进
在传统灰色关联分析方法(GRA)中,灰色关联度是通过求解每个输入变量与输出变量之间的关联系数得到的。然而,在有些情况下,历史数据对现有情况的影响程度是参差不齐的[7]。
另外,传统灰色关联度算法采用平权处理也存在以下问题:一方面,平均值忽略了各个影响因素的独特性,对于未来复杂变化情况的适应性较差;另一方面,当灰色关联系数较为离散时,总体关联度主要受关联系数大的数据的影响,从而导致分析结果出现偏差[8]。
利用纵向模糊加权和横向层次分析法(AHP)加权法对灰色关联度进行双向加权处理,从而减小误差。
1.1.1 纵向模糊加权法

(1)
式(1)中:i=1,2,…,m;t=1,2,…,T;w(t)表示纵向权值,反映了第t时间的影响因素指标i与j第个指标的关联系数λji(t)的权重。
纵向权值w(t)的计算方法如下。
(1)由于距离目前时间越近的数据,该数据对现有情况的影响程度就越大,即t1与t2的模糊互补优先关系矩阵F可以表示为
F=[ft1t2]T×T
(2)
式(2)中:ft1t2表示时间t1与t2的数据重要程度对比关系,且满足ft1t2+ft2t1=1。
当t1>t2时,表示历史时间的重要性大于t2的数据,令ft1t2=1;反之则ft1t2=0;当t1=t2时,表示历史时间t1数据的重要性和t2相同,令ft1t2=0.5。
(2)将模糊互补优先关系矩阵F=[ft1t2]T×T,改造成模糊一致矩阵S。
S=[st1t2]T×T
(3)
(4)
式中:t=1,2,…,T;k=1,2,…,T。
(5)
式(5)中:t1,t2=1,2,…,T。
(3)求纵向权值w(t)
(6)

1.1.2 横向AHP加权法
影响因素指标i与第j个指标之间的双向加权关联度Rij的计算公式为
(7)
式(7)中:i=1,2,…,m;j=1,2,…,T;σij表示横向权值,即影响因素指标i相对于第j个指标的重要程度。横向权值σij的计算步骤如下。
(1)梳理方案的方向目标,分析目标层、准则层、方案层的各层以及其内部因素关系,最终建立一种适应各种关系的评价模型。
(2)构造判断矩阵A=[aij]n×n,式中的aij表示第i个因素与第j个因素的重要程度对比。
(3)根据上述A的最大特征值λmax及其对应的特征向量w,将w进行归一化处理得到了w′,w′就表示该层次因素的权重。
(4)一致性检验。
计算一致性指标MCI:
MCI=(λmax-n)/(n-1)
(8)
根据阶数n查平均随机一致性指标MRI。
计算一致性比例NCR:
NCR=MCI/MRI
(9)
若NCR<0.1,认为判断矩阵的一致性可以接受,否则将进行修改[10-11]。
(5)综合各层次的权重,最后,以双向加权灰色关联度作为各因素对负荷影响程度的判定依据。
1.2 IPSO-BP算法
1.2.1 BP算法
BP神经网络[12-13](BPNN)是一种多层前馈网络的误差反向传播算法,由输入层、隐含层和输出层组成,如图1所示。

图1 神经网络结构示意图
BP神经网络算法的原理是根据基于最小误差原则,将网络的输出与期望输出间的误差作为一种不断更新权值和阈值的标准,当误差满足网络训练的误差目标设定值的上限,最终可以得到最优解,具体优化流程如图2所示。

图2 BP学习收敛过程
根据历史经验,可以根据式(10)确定隐含层神经元的个数:
(10)
式(10)中:NI表示BP的输入节点个数;NO表示输出节点个数。
BP神经网络具体的算法流程如图3所示。

图3 BP算法流程图
BP神经网络计算能力很强,可以模仿人脑的智能化处理方式,从复杂的非线性输入和输出信号中寻找规律。但在实际应用中,BP算法也存在以下缺陷:依靠经验去选择初始网络参数,缺乏统一的标准;当历史数据很多,就需要花费很长的学习时间,易导致误差收敛速度过慢;在训练和学习的过程中,易陷入局部极小值的问题等。因此利用改进的粒子群算法对BP神经网络进行优化,从而降低BP神经网络预测误差,使得预测结果更具有实际意义。
1.2.2 PSO算法
粒子群算法(PSO)作为一种全局随机搜索算法,适用于求解优化问题[14]。假设在D维搜索空间中,n个粒子组成了一个种群,Zi=(zi1,zi2,…zid)T表示第i个粒子在空间中的位置,Vi=(vi1,vi2,…vid)T表示第i个粒子的速度;Pibthest=(pi1,pi2,…,pid)T表示第i个粒子的最优的位置,即个体极值;Pgbest=(pg1,pg2,…,pgd)T表示该种群中所有个体经历过的最优位置,即全局极值。粒子群算法的本质就是通过这两个位置间的关系不断调整每个粒子的速度和位置:
vid=wvid+c1rand1()(pid-zid)+
c2rand2()(pgd-zid)
(11)
(12)
式中:w表示惯性权重;t表示当前迭代次数;c1、c2分别表示学习因子,取值范围(0,2];rand1、rand2表示(0,1]之间的随机数。
粒子在调整自己位置的过程中,通常还会受到最大速度vmax的限制,通常设定:
vdmax=mzdmax, 0.1≤m≤1
(13)
在每一次迭代过程中,粒子不断更新自己的速度和位置,个体极值和全局极值可以表示为
Pibest(t+1)=
(14)
f[Pgbest(t)]=min{f[pibest(t)]},i=1,2,…N
(15)
式中:f[Xi(t)]表示第t次迭代时,粒子Xi对应的适应度函数值。
1.2.3 IPSO-BP算法
在实际应用中,标准的PSO算法对BP算法进行优化存在一定的缺陷,粒子群通过速度变量改变当时的位移,而惯性权重的大小影响速度的快慢。惯性权重越大,在时间T内,粒子的运动位移就会越大。将粒子运动前和运动后的距离称为步长,因此粒子运动步长越大,更有利于进行全局搜索。惯性权重w对收敛速度有直接的影响,结合其运动原理,为使搜索按照先局部后全局再局部的方式进行,引入正弦函数([0,π]区间,先升后降),使粒子在刚开始时以一种较小的步长运动,并记录当前认为的最优值;之后逐步扩大步长,增强全局搜索能力,不断更新最优值记录;最后以一种较小的搜索能力精细查找,最终完成收敛。改进的权重公式为
w=wmin+(wmax-wmin)sin[(πt)/M]
(16)
式(16)中:wmax表示为权重的最大值;wmin表示为权重的最小值;t表示为迭代次数;M表示为迭代的最大次数。当t=2/M时,w=wmax;当t=M时,w=wmin。
针对物理学中位移和速度量纲不同的问题,引入时间因子。传统粒子群算法中的时间因子默认为1,导致粒子易在最佳位置附近振荡,无法及时寻找到最优解。因此可以引入与惯性权重和迭代次数相关的时间因子T,其表达式为
T=0.1+w
(17)
时间因子随着惯性权重大小的改变而改变,而惯性权重的大小和迭代次数有关,结合式(16)和式(17)可知,T从较小值开始逐渐增大,在迭代搜索中后期逐渐变小,当w最大值为0.9时,T变为最大值1。因此,随着迭代搜索时间因子的增大,有利于全局搜索最优解[15-16]。
IPSO优化BP神经网络:基于标准粒子群引入改进的时间因子和惯性权重w,并引入遗传算子以及马国庆等提出的速度边界限制和反弹策略,改进的粒子群优化3层BP神经网络算法步骤如下所示。
步骤1初始化BP网络,确定BP神经网络的层数以及各层的神经元个数。
步骤2粒子群的空间维度、粒子群的速度等参数进行初始化。
步骤3确定离子群的适应度函数,计算粒子的适应度。
步骤4对比个体粒子与种群的最优适应度的大小,筛选出最优适应度。
步骤5根据步骤1和步骤2更新粒子的速度Vi和位置Zi。
步骤6判断搜索次数是否达到了临界值或者目标函数是否最优,否则继续迭代。
步骤7将上述最优输出值作为BP神经网络初始权值和阈值,代入到BP神经网络中进行学习训练。
1.3 改进的GRA-IPSO-BP算法
用改进的GRA-IPSO-BP算法对电能替代潜力进行预测时,首先需要将电能替代潜力进行量化处理,则第t年的电能替代量可以表示为
(18)
式(18)中:α为电能替代量修正因子,根据浙江省能源消费情况,这里取0.03;De,t为电能替代量;Ye,t为第t年的实际电能消耗量;Ye,TB为基准年的实际电能消耗量;YTB为基准年终端能源消耗总量;Yt为第t年终端能源消耗总量。
然后,用改进的GRA算法从输入的影响电能替代潜力的指标中筛选出影响电能替代潜力的关键指标;将历史影响电能替代潜力的关键指标作为自变量,历史电能替代量作为因变量进行样本训练,使用IPSO算法对BP算法进行优化;最后进行IPSO-BP算法预测,将预测样本即影响电能替代潜力的关键指标输入预测模型,得到预测值,并进行误差计算。预测流程如图4所示。

图4 预测流程图
2 改进的GRA-IPSO-BP浙江电能替代潜力预测模型实证研究
2.1 数据输入
从经济因素、人口因素、政策因素、环保因素和电能替代技术因素等方面考虑,选取浙江地区2001—2017年的影响电能替代潜力指标数据:用电量、能源消费量、GDP、人口、CO2排放量、燃料、动力购进价格指数、电力固定资产投资、能源固定资产投资这9个因素作为输入变量,浙江地区的电能替代电量作为输出变量。首先用改进的GRA算法对影响浙江地区的电能替代潜力指标进行关键指标筛选,根据式(1)、式(7),计算出各影响因素对浙江地区的电能替代潜力的灰色关联度,如表1所示,从而筛选出影响浙江地区电能替代潜力的关键指标。
由表1可知,选择GDP、用电量、能源固定资产投资、电力固定资产投资作为影响浙江地区电能替代潜力的关键指标,并对数据进行归一化处理。
2.2 模型训练
上述归一化的数据中,将浙江地区2001—2017年电能替代电量和关键影响因素的历史数据代入IPSO-BP模型当中,调用训练函数对归一化后的历史数据进行训练,并得出电能替代电量预测结果。为了更直观地显示浙江地区电能替代电量预测拟合效果,将浙江地区2001—2017年电能替代电量拟合值与实际值绘制于图5中。
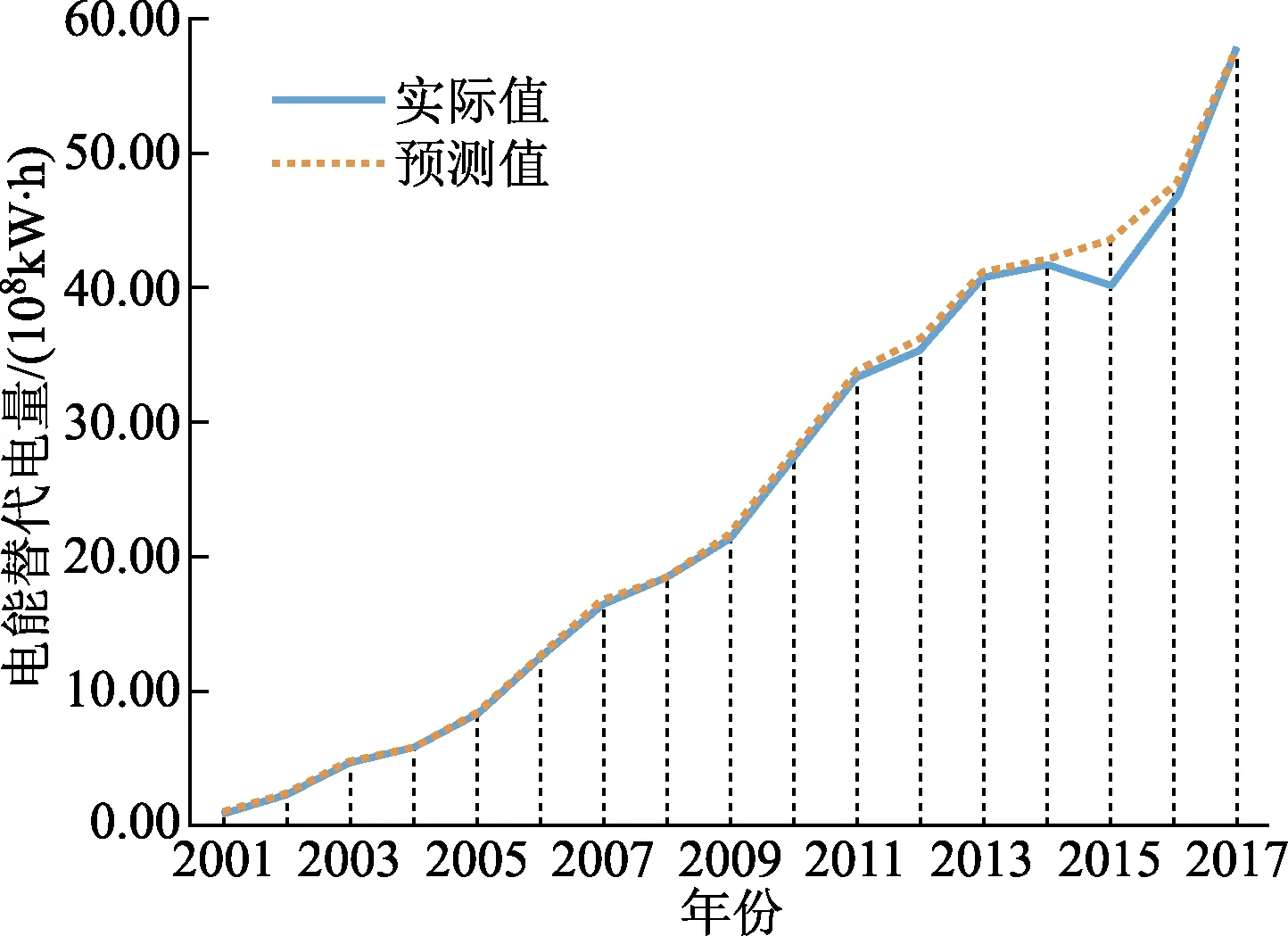
图5 预测拟合效果
根据式(19),求IPSO-BP预测模型的输出拟合值与电能替代电量实际值之间的相对误差e。
(19)
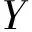
经计算得出,浙江地区电能替代电量模型输出拟合值与电能替代电量实际值之间的平均相对误差为2.80%。
将训练样本分别代入到BP模型、PSO-BP模型中进行测试,测试结果如图6所示。
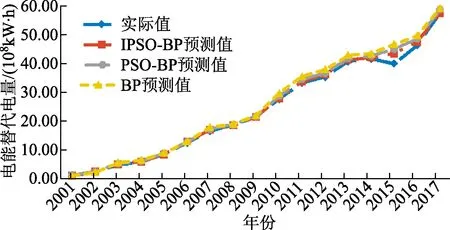
图6 模型预测拟合效果对比
观察图6可知,BP的平均相对误差最大,计算结果为7.40%,IPSO-BP的平均相对误差最小,计算结果为2.80%,说明IPSO-BP拟合程度优于PSO-BP和BP,且具有更小的相对预测误差,说明IPSO算法可以在很大程度上提高BP算法预测精度,IPSO-BP预测模型能够较好地实现浙江地区电能替代电量预测。

表1 各影响因素电能替代潜力的灰色关联度
2.3 预测结果分析
由改进的GRA-IPSO-BP模型得出浙江地区2018—2022 年电能替代电量预测结果,如表2、图7所示。

表2 2018—2022年电能替代电量预测结果
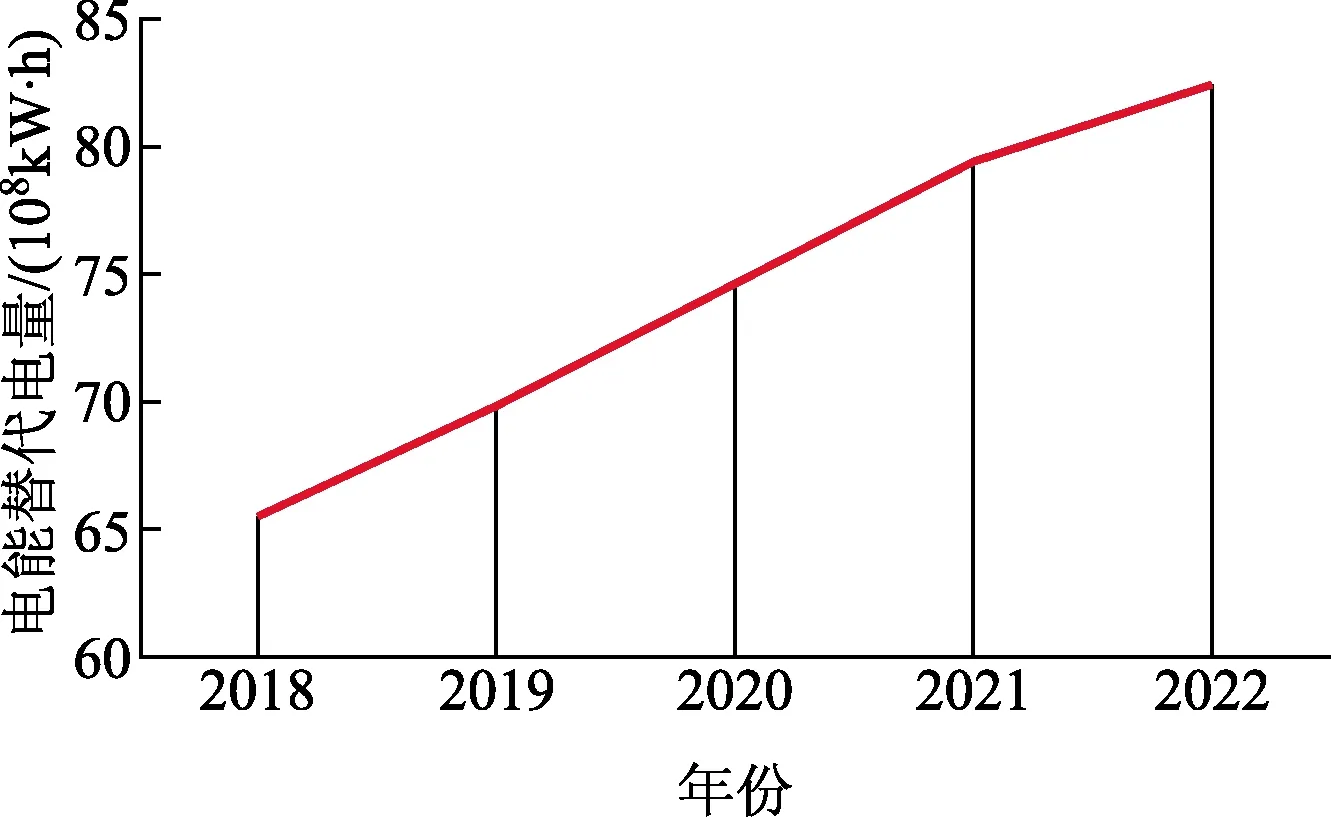
图7 2018—2022 年电能替代电量预测结果
由表2、图7可以看出2018—2022年,浙江地区的电能替代电量总体呈上升趋势,随着电能替代战略的深入推进,浙江省电能替代潜力不断增强,未来的电能替代电量发展保持着较快的速度增长。
3 结论
将改进的GRA-IPSO-BP模型应用于浙江电能替代潜力的预测工作中,提出了一种基于改进的GRA-IPSO-BP浙江电能替代潜力预测方法。得到了以下结论。
(1)首先将电能替代潜力进行了量化处理,从经济、政策、环保、电能替代技术等因素考虑选取了影响电能替代潜力的指标。
(2)然后用改进的GRA算法筛选出影响电能替代潜力的关键指标,最后用IPSO-BP算法进行了浙江地区的电能替代潜力预测,将预测结果进行了对比分析。
(3)实例结果表明,在预测电能替代潜力时,GRA-IPSO-BP预测模型明显优于PSO-BP和BP预测模型,在实际应用中具备可行性。

