隧道塌方应急救援多车型调度模型

崔洪军，杨 颖，朱敏清，李 霞

(河北工业大学土木与交通学院，天津 300401)

隧道塌方事故以其高发性、高危性，严重威胁着隧道施工安全。数据表明，2006—2016年间，在中国发生的施工期间隧道塌方事故49起，死伤人数高达255人[1]。事故发生后的应急救援车辆调度问题是救援工作的核心。

应急车辆调度问题是传统车辆路径问题在应急情境下的一种演化。对于不同的应急情境，路径规划时交通阻抗的计算方法不尽相同。学者大多以历史拥挤度或实时路况为依据，结合车流波动理论、路阻函数理论，分析道路现有车辆对应急救援车辆行驶时间的影响。如：Zhao等[2]以最短的行车时间为目标，建立应急车辆的动态路径优化模型；Panahi等[3]基于GIS利用Dijkstra算法获取应急车辆的最短路径；刘春年等[4]提出了基于路阻函数理论与Dijkstra算法相结合的最优路径数学模型。Vlad等[5]利用应急车辆和道路十字路口的GPS工具获取实时交通状况，使用人工神经网络方法获得应急车辆的最短路径；阎俊爱等[6]基于实时的复杂道路状况，改进了遗传算法，求解动态条件下的最短路。也有学者考虑到山区路网道路条件的复杂性，将车道数、时间段、路面状况等条件考虑到交通阻抗中，通过引入权值k对交通阻抗进行修正，得到道路的综合权值[7-8]，再进行路径规划。

综上，目前针对救援车辆调度问题的研究大多直接等同于最短路算法，并且没有考虑到救援车辆类型不同的问题。应急救援车辆主要包括救护车、工程救险车、吊车等特种车辆，它们本身存在车体超高超宽、载重较大的特点，对道路条件有特殊要求。同时，由于在建隧道多设于地形偏袒的路段，周边道路条件复杂，甚至存在不能通行的路段，复杂的道路环境对应急救援车辆的行驶造成较大影响。针对塌方事故应急救援车辆调度的这些特点，分车型地进行救援车辆调度研究，为塌方事故救援方案的制定提供一定支持。

1 应急车辆路径选择

1.1 符号说明

设I为车辆供应点集合，EVK为应急救援车辆集合，EVi,EVj∈EVK，i,j∈I; 设路网G=(V,E),E为道路网络中节点之间边的集合，a为路网中的路段，a∈E；V为路网中节点的集合，假设车辆供应点为路网中的部分节点，即I⊆V。

1.2 应急车辆分类

根据应急车辆的组成，将车辆分为普通车辆、超限车辆和重载车辆三类，具体车型特征如表1所示。

表1 应急救援车辆分类

注：限高H、限重F的大小取决于实际救援车辆的属性。例如：若车辆高3 m，则路径中不应包含限高小于3 m的路段；若车辆载重35 t，则路径中不应包含限重小于35 t的路段。

1.3 应急车辆路径规划模型

选取道路限高、限重情况和路段是否可通行3个因子作为应急车辆对道路的限制因素；选取路段长度、道路等级、拥堵情况、路面状况和路段坡度5个因子作为影响道路综合权值的考虑因素。以此为基础建立应急救援车辆路径规划模型。

路段a是否通行的限制条件可表示为

Ma={hl，wl，rl}

(1)

式(1)中：Ma表示路段上的限制因素；hl表示路段的高度限制(H)；wl表示路段的载重限制(T)；rl表示路段是否可以通行。具体描述如式(2)～式(4)所示。

(2)

(3)

(4)

救援车辆EVi对道路的限制因素表示为M，对M≤Ma，定义如下：

(5)

WEVi=f(l,g,b,s,p)

(6)

式(6)中：WEVi为车辆EVi路径的综合权值；l为路段长度；g为道路等级；b为拥堵情况；s为路面状况；p为路段坡度。则考虑综合权值的应急救援车辆路径规划模型为

(7)

s.t.∀a∈E,M≤Ma

(8)

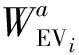
1.4 模型求解

1.4.1 道路因素权重分配

不同道路因素对不同车型产生的影响程度不同。利用层次分析法确定各指标权重。对20位专家的判断矩阵进行计算处理，并进行一致性检验，得到不同车型的道路因素权重系数如表2所示。

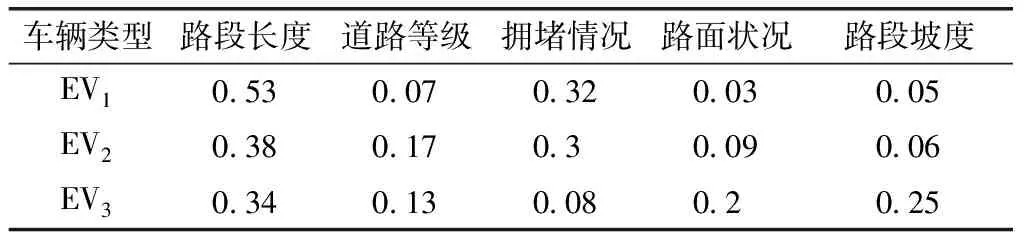
表2 道路因素权重系数

1.4.2 道路因素无量纲处理

(1)路段长度

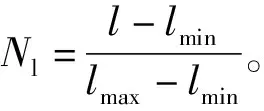
(2)道路等级g、拥堵情况b、路面状况s

依据等级越高，权值越小的原则对不同道路因素进行赋权[9-10]，如表3所示。

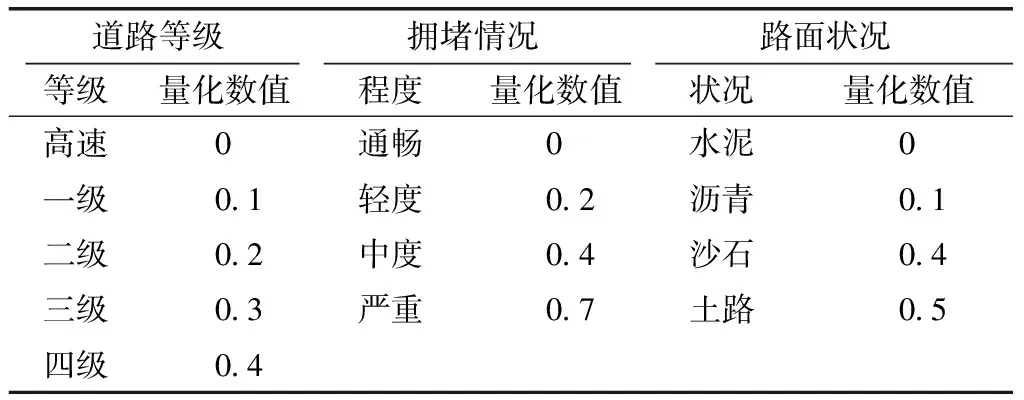
表3 道路因素赋权

(3)路段坡度

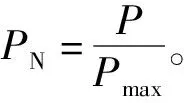
2 车辆供应点评价

假定不同类型救援车辆从同一车辆供应点同时出发，超限或重型车辆由于车体大，在道路上行驶所占空间大，其变道、加速减速等行为会影响其他车辆行驶。研究认为从路径重合度越低的车辆供应点调度，车辆之间的干扰小，该供应点越优。

分别计算每个车辆供应点三种车辆之间的路径重合率，并计算平均值，如式(8)、式(9)所示：

(9)

(10)

式中：REVi-EVj表示车辆供应点中每两种车型之间的路径重合率；NEVi、NEVj表示车辆EVi、EVj分别所经过的路段数；Ri表示车辆供应点i的平均路径重合率。

3 应急救援车辆调度模型

3.1 模型建立

在求得应急救援车辆路径的基础上，需要对车辆进行合理的配置。车辆调度时间是指从第一辆车辆派出开始，到所有应急车辆到达事故现场所经历的时间[11]，因此整个应急车辆调度时间为最后一辆到达塌方地点的车辆所需时间。应优先考虑从到达事故点最快的地点调车，在到达时间相同或者相差不大时，优先选择路径重合率低的车辆供应点。

假设在最优路径上行驶时，不同类型车辆的平均速度相同。根据第1节求得的路径，可计算从车辆供应点i出发的k型车辆到达事故点的时间tik：

tik=Lik/v

(11)

式(11)中：Lik表示从车辆供应点i出发的k型车辆的路径长度；v表示车辆平均行驶速度。

以最后一辆车辆到达时间最小为目标，满足时间、车辆数量等约束，结合车辆供应点评价结果，构建应急救援车辆调度模型，如式(12)所示：

(12)

此模型表示在满足应急限制期的条件下，优先选择从车辆到达时间短的供应点调度车辆，到达时间相同或相差在θ以内时，比较相应车辆供应点的路径重合率，选择较小者。最终得到的多车型调度方案的完成时间为各单一应急车辆调度方案中车辆到达时间的最大值。

3.2 模型求解

采用文献[12]的思想求解该模型，具体步骤如下。

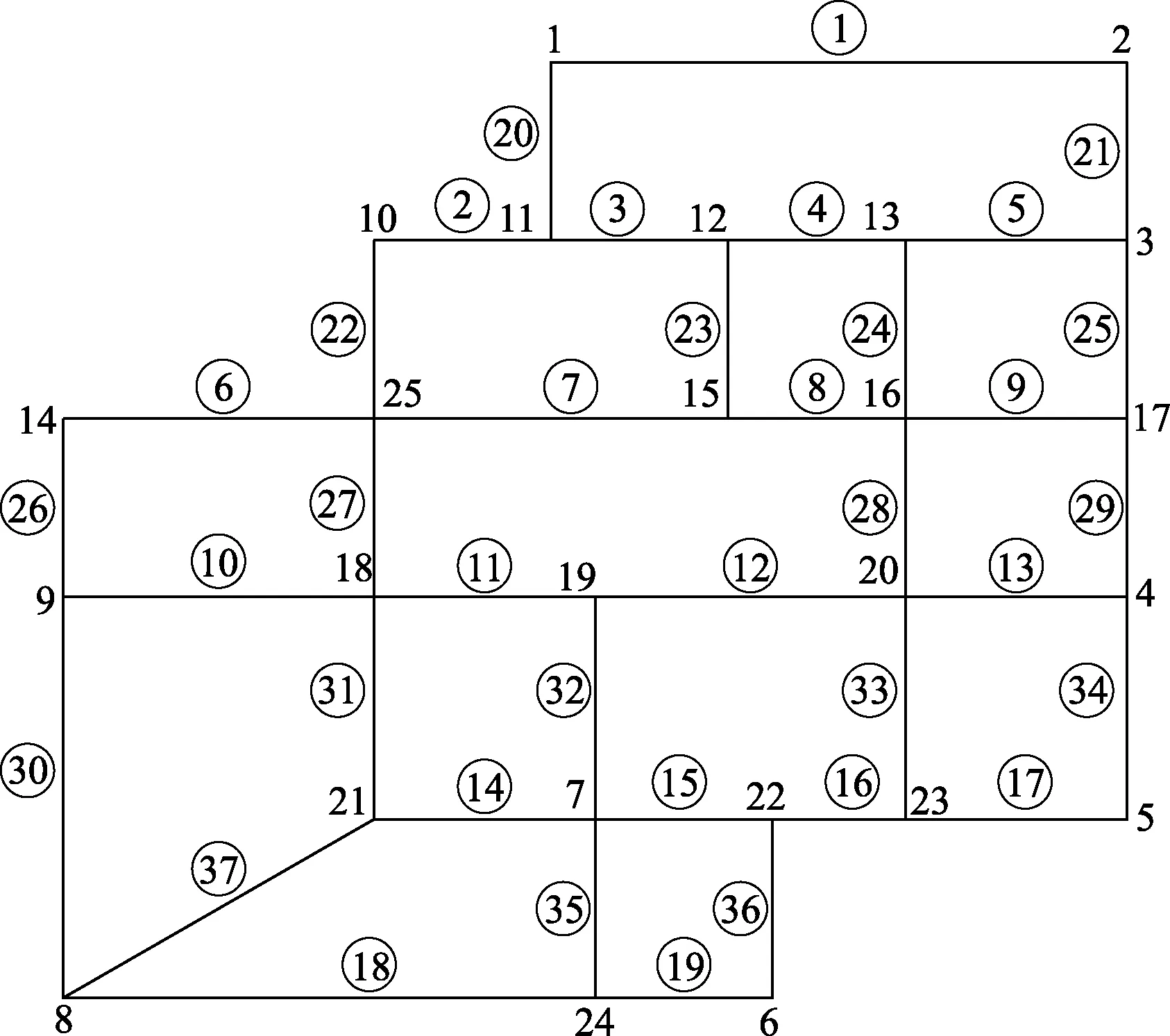
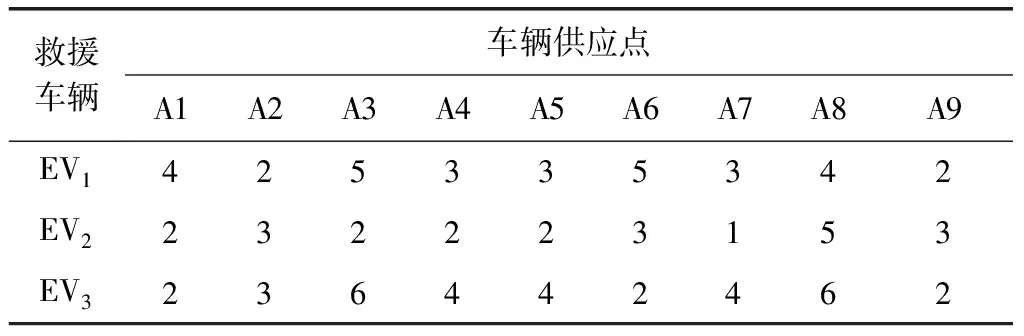
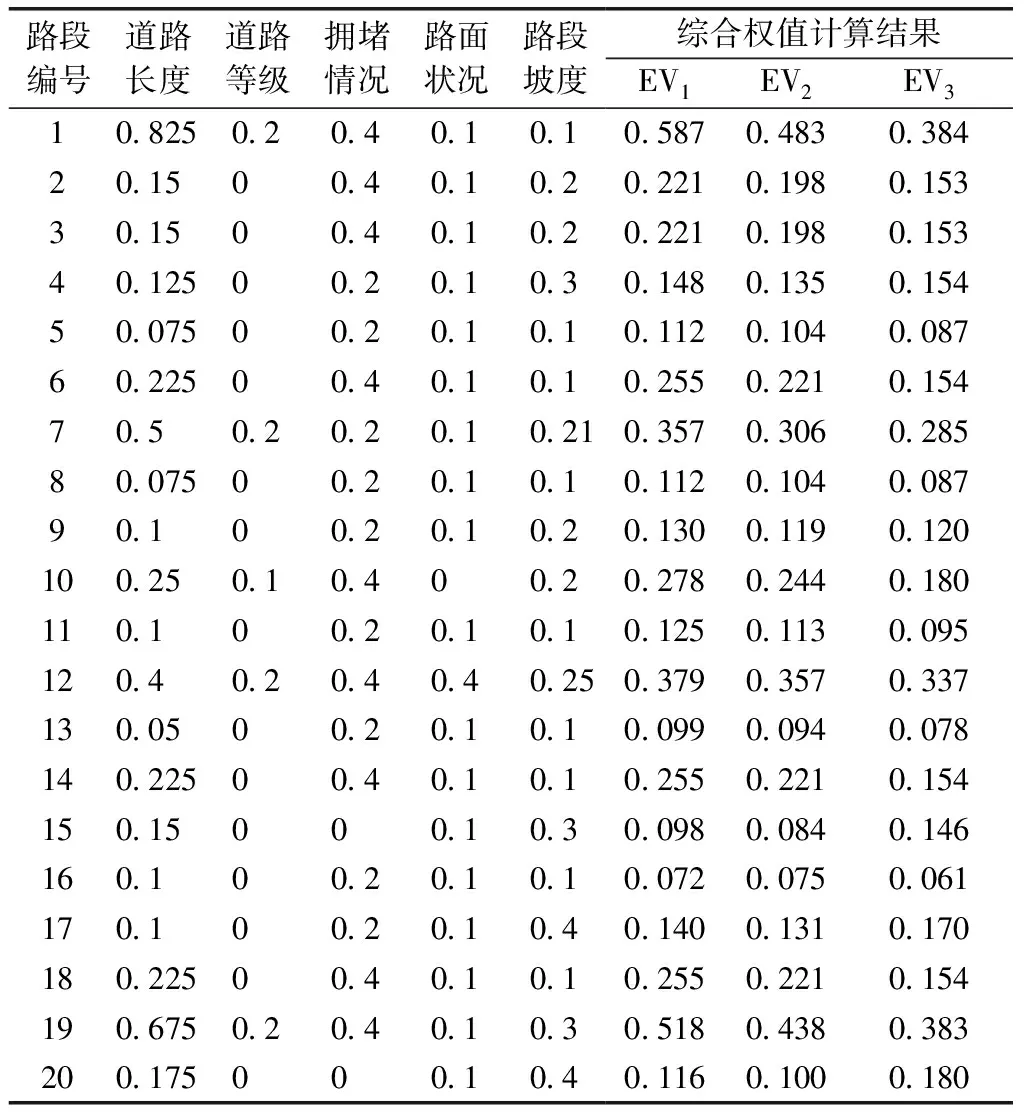
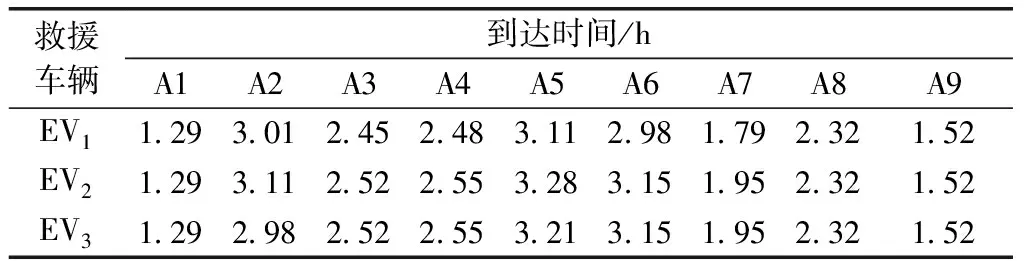
(1)对于k型应急救援车辆，把tik按从小到大排序，若tik相等或相差小于或等于θ，则按Ri从小到大排序，得到：te1k≤te2k≤…≤tepk≤T

(3)分别对于所有车型重复(1)、(2)，可求得各单一车辆调度方案φ1,φ2, …,φk, 从而得到多种车型调度方案φ=[φ1,φ2, …,φk]，且T(φ)=tm=maxT(φk)。

4 模型解析

以某在建隧道周围路网为例，分别对路网的节点和路段单元进行编号，如图2所示。该路网中包含25个节点，37个道路单元，事故隧道位于节点25附近，其中路段4、11、12、35设有限高标志，超限车辆无法通过；路段5、17、28、30设有限重标志，重载车辆无法通过。节点1～节点9为应急车辆供应点，记为A1～A9。假设塌方事故现场需要13辆救护车等普通车辆，10辆吊车等超限车辆，25辆运输物资的重型车辆。各车辆供应点拥有的三种类型车辆数如表4所示。

图2 路网拓扑图

表4 应急车辆供应点信息

4.1 车辆路径选择

依据1.4.2节，对道路各因素进行处理和赋权，计算得到三种车型在每条路段上的综合权值。由于篇幅有限，列出路段1～20的计算结果，如表5所示。

设定救援车辆平均行驶速度为45 km/h。根据第1节求得的路径及式(11)，可计算得到从车辆供应点车发的不同类型车辆到达事故点的时间以及各车辆供应点的路径重合率，结果如表6、表7所示。

表5 三种车型道路综合权值计算结果

表6 车辆到达时间

表7 路径重合率平均值

4.2 车辆调度方案

取θ=5，即到达时间相差5 min以内的两个车辆供应点视为到达时间相同。对于应急限制期，中国并没有明确地规定，考虑到隧道所处位置一般距市区较远，结合以往隧道塌方事故救援案例，设定应急限制期T=3.5 h。根据第3节车辆调度模型，可得调度方案如表8所示。

以救援车辆EV1为例，从调度方案可以看出，对于救援点A1，车辆到达时间最短，故优先调配A1的所有车辆；救援点A7、A9的车辆到达时间相差较小，由于A7的路径重合率明显低于A9，故优先选择从A7调度车辆。另外两种类型车辆的调度方案也符合这一规律。可得多车型调度的总时间为3.11 h。

表8 调度方案

5 结论

针对施工中的隧道塌方事故救援车辆调度问题中面临的周边道路条件复杂和救援车辆种类特殊的问题，主要得到如下结论。

(1)针对三种类型救援车辆，综合考虑路段长度、道路等级、拥堵情况、路面状况和路段坡度五个因素对路段综合权值的影响，并基于车辆自身对道路的限制因素进行路径规划。

(2)建立了应急车辆调度模型，以车辆到达时间最短为前提，计算了不同车辆供应点出发的车辆之间的路径重合率，能进一步地避免车辆路径之间的相互干扰，提高救援效率。在最短时间内保证救援车辆的到达。