“设问诱导+自主学习”教学实例探究*

江西省萍乡市萍乡中学(337000) 许雪荣

1激发兴趣,课前设问诱导学生自主学习

问题(1): 你见过心脏线、玫瑰线、阿基米德线、笛卡尔线、雅各布线等优美的曲线吗?请在网上自我搜索并了解相关知识.

问题(2):“绿水青山就是金山银山”的理念已融入我们的日常生活中,我们班有的同学们喜欢骑自行车来上学,值得提倡.请思考以下这个问题: 自行车店在销售时,以高出进价的50%标价,若按标价八折销售与直接降价300 元销售,获利相同,请问自行车进价是多少?

问题(3): 学校高一每年要举行羽毛球比赛.为迎接比赛同学们要加强训练,现班上要采购一批羽毛球,班长决定在网店上采购,若花255 元可采购2 筒甲种羽毛球和3 筒乙种羽毛球(甲种羽毛球每筒的售价比乙种羽毛球多15 元).你知道网店上甲、乙两种羽毛球每筒的售价吗?若采购总数满10 筒则网店可优惠促销(甲种羽毛球降价10%,乙种羽毛球降价5 元),你手中有430 元班费,你如何采购这批羽毛球?

我一般采用“课前三问”进行设问诱导学生自主学习,课前设问不宜太多,也不宜太难,问题的设计一定要考虑是否有“兴趣点”、“吸引力”、“实例值”.问题(1) 主要是吊学生的胃口,当他们听到这些好听好浪漫的名词时,难免不产生好奇心,促使他们主动上网去查询并了解到各种各样的函数及其图像,自然而然地就会有学好函数知识的冲动,做好了严阵以待的准备,起航吧.问题(2) 与问题(3) 主要从学生身边的活生生的事例出发,同时又考虑到初中知识的过渡,承上启下,让学生敢于提出变量x或y去解决实际问题,初步奠定函数变量概念,这样就有利于课堂导学.

2积极诱导,课中发挥学生的主观能动性

我们教学要真正做到“问题导向”模式,一定加强对学生的“会学”指导,“授之以鱼, 不如授之以渔”,“会学”比“学会”更重要.“会学数学”应包括: 阅读理解、质疑提问、梳理总结、表达交流等环节,我们要坚持“先学后教”,放手让学生先自己去学,去发现问题,提出问题,然后在课堂上与学生一起探讨并解决学生发现或存在的问题.我推荐高中数学大单元(章、单元、节、时)问题导向设计的教学序列化、整体化,指导教师科学地制定设问导学案.而设问导学案也作为翻转课堂的重要工具,将知识问题化,以问题为主线,帮助学生自主学习,发挥他们的主观能动性.那么如何进行设问诱导呢?下面本人以一份设问诱导的导学案进行解读:

§1.2.1 函数的概念(第一课时,自主探究学案一)

一、温顾而知新篇

问题1: 是否记得初中的函数概念呢?那个叫自变量,那个叫因变量?

问题2: 我们初中学过几个函数?能写出他们的关系式以及画出他们的简单图像吗?

问题3: 初中学过的分式,平方根式有什么要注意的吗?

二、新知探究篇

问题1: 请观察下面几个图表,看能否得出它们的共同特点是什么?

请填空并思考问题: 共同特点: 对于集合A中的任何一个数,集合B中都有____和它对应.这种特点是不是与我们初中所学函数概念一致呢?如果一致的话,能否用刚学过集合概念加以重新定义函数概念呢?

请大家带着以下问题去阅读教材填写以下空格并思考问题:

1 函数的概念

一般地,设A,B是两个____,如果按某种____的对应关系f,对于集合A中的____元素x,在集合B中都有____的元素y和它对应,那么这样的对应f:A →B叫做从____到____的一个函数,记作:____,____. 其中,所有自变量x组成的集合A叫做函数f(x)的____,与之相对应的函数值y组成的集合叫做函数f(x)的____.

思考问题(1): 定义域和值域可以为空集吗?

(2): 值域C={f(x)|x ∈A}与集合B的关系是____;

(3): 函数三要素是指函数的____、___和____.

(4): 试问下面两关系式x= 1,y= 1 是否为函数关系式?

(5): 请用集合的形式分别写出初中学过的几个函数的定义域和值域

函数名称?关系式定义域值域

2 区间的概念与表示

(1) 一般区间表示: 设a,b ∈R,a ＜b,规定如下:

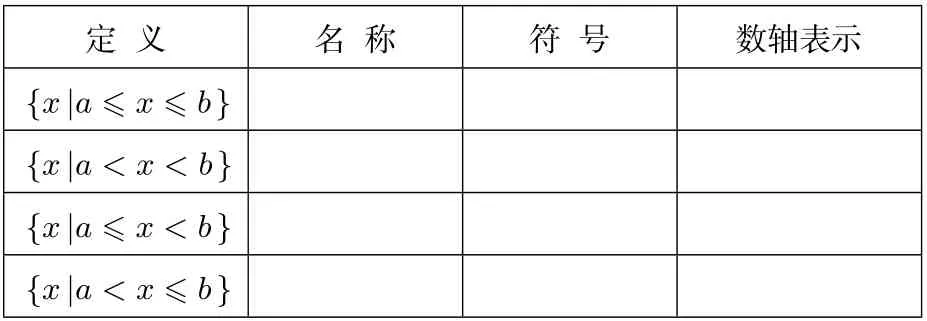
定义名称符号数轴表示{x|a ≤x ≤b}{x|a ＜x ＜b}{x|a ≤x ＜b}{x|a ＜x ≤b}

(2) 特殊区间表示

定义{x|x ≥a}{x|x ＞a}{x|x ≤a}{x|x ＜a}_符号

思考问题(1): 区间(a,2-a)中的实数a有什么要求吗?

(2): 区间是集合吗?请说出它们之间的关系并用数学符号填空:

(a,b)____(a,b]____[a,b];

(a,+∞)____[a,+∞);

(-∞,b)____(-∞,b]____(-∞,+∞).

三、学以致用篇

问题一: 请判断下列对应关系f是否为从集合A到集合B的函数.

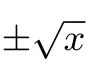
(2)A=N,B=R,x ∈A,f:x →|x-2|;

(4)A=[-1,1],B={0},x ∈A,f:x →0.

请问不是函数关系式的,理由是什么?

问题二. 设集合M={x|0 ≤x≤2},N={y|0 ≤y≤2}, 给出下列4 个图形, 其中能表示集合M到N的函数关系的有____.

请问未选项违背了什么规则?

问题三: 求下列函数定义域,并用区间表示:

请思考还有什么会对自变量有限定的要求?可展开讨论.

请问赋值法计算能否求出f(f(x))的关系式?

问题五: 下列哪一个函数与函数y=x是同一个函数?

请总结函数关系式是同一个函数必须满足几个条件?

四、自我提高篇

问题一: 下列对应或关系式中是A到B的函数的有____.

(1)A=B={x|-1 ≤x≤1},x ∈A,y ∈B,f:x2+y2=1;

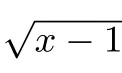
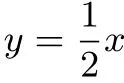
(4)A={1,2,3,4},B={0,1,2},对应关系如图1 所示;

图1

问题二: 分别用集合、区间两种方式表示下列函数定义域:

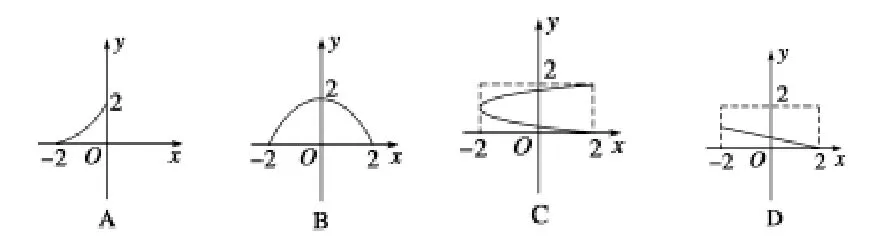
问题三: 若函数y=f(x) 的定义域为M={x|-2 ≤x≤2}, 值域为N={y|0 ≤y≤2}, 则函数y=f(x)的图象可能是()

问题四: 已知f(x)=3x2-5x+1.

(1) 若f(a)=2,求a的值;

(2) 若g(x)=x+1,求f(g(2))的值.

五、团结协作篇

请各学习小组展开讨论并探求该函数的某一性质?然后总结出小组成果予以展示.

六、自我总结篇

通过你的自主学习与今天的讨论,你有何收获,试写出你的几点感受与同学们一起分享: (大家可以各抒己见)

3 团结协作,让学生享受成功的体验

数学教学需要教师为学生创自主、合作的学习环境,关注学生的自主探索与合作交流,让他们真正成为学习的主人.在实际教学中,小组合作学习是否有效,很大程度上取决于自主学习是否有效.培养学生“学会学习、学会交流、学会合作”也是当今教学改革最核心的目标.因此,能够激发学生的兴趣和热情,也有利于提高学生应用数学的能力.正如经济合作与发展组织在其开展的国际学生评估项目(PⅠSA 项目)中认为: 面向未来而化解问题的创新能力远比复制既往的知识更具建设性价值,强调个人在面对不可预测的复杂情境时,灵活“分析、推断和沟通”的创意能力,特别是基于独立人格、自由思考而做出自主判断、自主选择的发展性探究能力.我们新时代教育工作者应该深知学生的创新发展能力的培养要在我们平常的日常教学中经常去设计学生探究、合作、交流的平台,基于数学核心素养的教学要求教师提供时间和空间给学生自主或团体探究感兴趣的现实问题,学生在这个探究的过程中经过自主探索和合作交流,有助于他们在数学知识与其应用之间建立即时联系.

再如: 有一次我和学生一起在学校运动场踢足球时,出现了一个令人赞叹的一幕,我班的“足球先生”从边线带球往前冲,突然急停,一个大脚长距离吊入球门,一道弧线划过直入球门里,同学们高兴大叫: 足球先生!金球!金球!第二天一上数学课时我即时抛出下面这样一个问题: 同学们,请大家分组讨论我们踢足球时,在边线运球射门,什么位置射门命中率最高(假设球直线飞行,不含香蕉球)?这一下课堂上气氛高涨,讨论热烈,好多学生竟然不知道标准足球场的尺寸以及球门的尺寸等等知识, 小组成员分分上网查询和设计,最后形成团队合作成果:

知识材料正规足球场大小: 长105 米、宽68 米;球门:长7.32 米、高2.44 米;大禁区(罚球区): 长40.32 米、宽16.5米, 在底线距离球门柱16.5 米; 小禁区(球门区) : 长18.32米、宽5.5 米, 在底线距离球门柱5.5 米; 中圈区: 半径9.15米;角球区: 半径1 米,距离大禁区13.84 米;罚球弧: 以点球点为中心,半径9.15 米的半圆;点球点: 距离球门线11 米.

设计如图2: 我校足球场长105米, 宽68 米, 球门宽7.32 米. 某足球先生从中场开始沿边线直线奔跑运球,问: 在何处急停远射,球入空门的命中率最高?(球门高、射门力度等因素不计,球直线飞行)

图2

解析据实践经验及理想化的设计可知,该入射点对球门两端所张的角度越大则命中率越高.

创造来源于实践.我们老师要在日常生活实践中善于发现并捕捉这些数学模型材料,并引导学生展开团队合作去探究其中奥秘.这样学生的积极性就更高,在不知不觉中我们就培养了学生的创造性思维与探究科学真理的勇气等等.这就是我们现在教育所追求的目标之一.