充分预留思考切口,真实测评数学素养

广东省中山市坦洲实验中学(528467) 邓凯

2019 年广东省初中学业水平考试数学卷第23 题的第(3)小题是一道看似平常的题,但笔者抽查考生该题的答题情况后回头琢磨该题的图形结构及已知数据,才体会到命题者编制这道题时下足了功夫,这道题不失为一道好题.该题考查考生根据已知面积关系建立数学模型的能力,进而测评考生的数学建模、直观想象、数学推理以及数学计算等数学核心素养.考生解答时能否找到思考的切入口?能否根据试题搭建的模板建立模型?能否在推理比较中优化思维进而寻求最优解?这些都能体现考生之间数学素养的差异.就本题而言,命题者为考生预留了多个思考的切入口,搭建了多个数学模型的模板,提供了充足的思考空间,为学生展示其数学素养提供了充足的条件,因此能保证测评考生数学素养的信度和效度,从而更真实地测评出学生数学素养的发展情况.

1 试题呈现

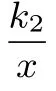
(2) 求这两个函数的表达式;

(3) 点P在线段AB上,且SΔAOP:SΔBOP=1:2,求点P的坐标.

图1

图2

参考答案: (1) 略;(2) 略;

(3) 如图2,连接OP、OA、OB,设直线y=-x+3 与x轴交于点C.

当y=0 时,x=3,

∴点C的坐标为(3,0).

∵点P在线段AB上,设P的坐标为(m,-m+3),

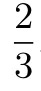
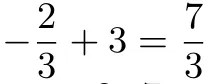
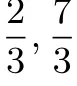
2 试题评价

这道试题比较常规,考查的知识点都是初中数学中的基础知识与核心思想方法,包括一次函数、反比例函数、函数与不等式之间的关系、三角形的面积等知识,以及数学建模、待定系数法、转化与化归等数学思想方法.从考生答题情况来看,大多数考生都能解答第(1)小题和第(2)小题,能顺利解答第(3)小题考生不超过半数.本题对学生数学核心素养的考查具有合理的区分度.

从考查学生数学核心素养的角度看这道题,第(1)小题主要考查学生直观想象素养,当学生理解了根据图象理解函数与不等式之间的关系之后,直观函数图象即可得到答案;第(2)小题主要考查学生的数学运算素养,当学生理解待定系数法求函数解析式之后,通过简单的解方程和解方程组即可得到答案;第(3)小题能够综合考查学生数学建模、直观想象、数学推理和数学运算等数学核心素养,已知条件中给出两个三角形的面积的比,可利用转化与化归思想将三角形的面积之比变为两条线段的长度之比,还可以转化为求两条线段的长度,部分数学素养突出的考生还可以直接通过“分点”的性质建立模型.事实上,该题为考生预留了多个思考切入口,考生任意选择其中一个切入口,只要具备相应的直观想象素养皆可建立数学模型,只要具备数学推理和数学计算素养就能顺利解答本题.

另外,本题图形简洁,计算量很小,为数学核心素养的测评减少了干扰因素.

3 试题多解

整理抽查的1000 份考生答卷情况,不同于标准答案且符合学生学段认知的自然解法主要有以下四类六种.

第一类(选择“面积关系”列式): 思路类似参考答案,设点P的坐标之后由面积之比列式计算.

解法一(直接求线段AP和PB的长): 如图3, 连接OP、OA、OB,

设直线y=-x+3 与x轴交于点C,与y轴交于点D,设P的坐标为(m,-m+3).

当y=0 时,x=3,当x=0 时,y=3,

∴点C的坐标为(3,0),点D的坐标为(0,3).

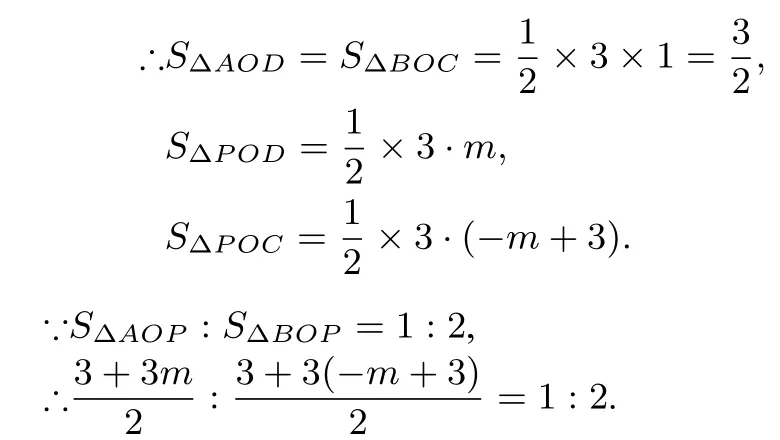
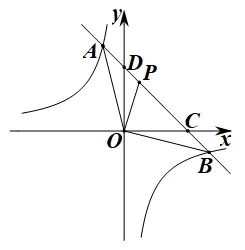
图3

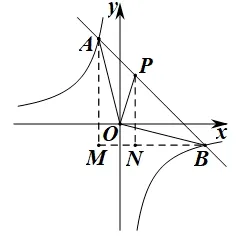
图4

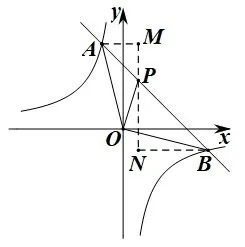
图5

第二类(根据“线段长度”列式): 思路是由面积之比转化得到线段之比,设点P的坐标之后由线段之比列式计算.

解法二(直接求线段AP和PB的长): 如图2, 连接OP,OA,OB,

∵SΔAOP:SΔBOP=1:2,

∴AP:PB=1:2.

∵点P在线段AB上,设P的坐标为(m,-m+3),

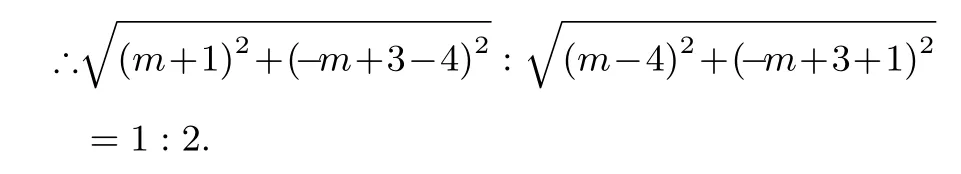
整理,得(m-4)2=4(m+1)2,

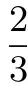
有考生用同样的方法根据AB和PB(或AB与AP)的长度之比列等式求解,但过程比解法二稍微复杂一些.

解法三(构造直角三角形求线段AP和PB的长) :如图4, 连接OP,OA,OB, 过点A,P分别作x轴的垂线,与过点B作x轴的平行线交于点M,N. 设P的坐标为(m,-m+3),

∵AM=BM=5,

∴ΔABM和ΔPBN都是等腰直角三角形.

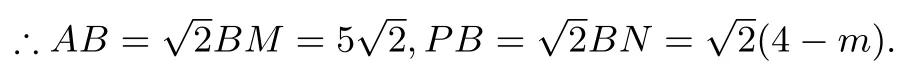
∵SΔAOP:SΔBOP=1:2,

∴PB:AB=2:3.

第三类(根据“线段之比”构建相似三角形): 思路是由面积之比得到线段之比, 再根据线段之比构建相似三角形,设点P的坐标之后由线段之比列式计算.

解法四如图4,连接OP,OA,OB,过点A,P分别作x轴的垂线,与过点B作x轴的平行线交于点M,N.设P的坐标为(m,-m+3),

由辅助线的作法可得ΔBAM∽ΔBPN.

∴BN:BM=BP:BA.

∵SΔAOP:SΔBOP=1:2.

∴BN:BM=BP:BA=2:3.

∴(4-m):5=2:3.

有考生过点P作x轴的平行线, 类似地根据AP和PB(或AB与AP)的长度之比列等式求解,但过程比这种解法四稍微复杂一些.

解法五如图5,连接OP,OA,OB,过点A,B分别作x轴的平行线,与过点P作x轴的垂线交于点M,N.设P的坐标为(m,-m+3),

由辅助线的作法可得ΔAPM∽ΔBPN.

∴AM:BN=AP:BP.

∵SΔAOP:SΔBOP=1:2,

∴AM:BN=AP:BP=1:2.

∴(m+1):(4-m)=1:2.

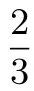
有考生由ΔAPM∽ΔBPN得PM:PN=AP:BP,然后列式求解的,与解法五基本上是一样的.

第四类(根据等分点性质计算): 思路是由面积之比得到点P为线段AB的三等分点,再三等分点的性质计算出点P的坐标.

解法六如图4,连接OP,OA,OB,过点A,P分别作x轴的垂线,与过点B作x轴的平行线交于点M,N.

由辅助线的作法可得ΔBPN∽ΔBAM.

∴BN:BM=BP:BA.

∵SΔAOP:SΔBOP=1:2,

∴BN:BM=BP:BA=2:3.

即点N为线段BM的三等分点.

∵BM=5,

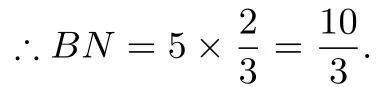
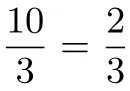
以上六种解法, 从不同角度展示了学生良好的数学建模、直观想象、数学推理以及数学计算等数学核心素养.一方面,说明这道题是一道好题,既能促成学生数学素养的展示,又能区分不同数学素养的差异,另一方面,我们在平时的教学中要善于运用类似的问题充分引导学生进行创新探索,充分发展他们的数学素养.

4 教学建议

本文所论述的这道题属于“数学建模型”类问题.基于本题及学生答题情况的抽样调查研究,笔者认为在数学建模类问题解决的课堂教学中至少应该做好三个方面的工作:

4.1 引导学生实现“思维突破”

笔者抽样的1000 名学生本题的得分情况如表1:

表1 2019 年广东省初中学业水平考试数学科第23 题得分抽样调查统计表

按照评分标准,考生做对第(1)小题得2 分,做对第(2)小题得4 分,做对第(3)小题得3 分.从上表可以看出,本题得满分的人数只占14%,也就是说就本题考查的数学素养而言,达到考查最高要求的人数并不多.再看得分为7-9 分的人数的百分比发现,能做第(3)小题并且能得分的考生约占或者略超27%,这就是说大多数学生的数学建模或者与本题模型相关的直观想象等素养是较弱的,他们存在的问题往往是解决问题时找不到思考的切入口,难以实现“思维突破”.因此,提升学生数学核心素养使其由弱到强,抓根务本的方法就是引导学生解决问题时能够找到问题的切入口并实现“思维突破”.以本题的教学为例,教师可能通过“独立解决”“小组合作”“成果展示”等活动引导学生分别将“面积之比”“线段之比”“线段长度”“三等分点”作为建立模型的模板作为切入口,之后不仅让学生从不同的切入口建立模型,还要理解各个切入口之间的转换关系,形成并积累寻找切入口的经验.引导学生“思维突破”时,可以引导学生根据各模板选择或者构造不同的几何基本图形建立数量关系.“思维突破”的过程有时是有规律可循的,有时是有灵感的,但都需要学生勇敢地、专注地、执着地甚至急切地寻求解决思路.

4.2 激发学生坚持“思维优化”

我们在平时的观课议课中发现,一些不注重提升学生数学素养的课堂,教师和学生都是习惯于解决多个问题,每个问题都以解决为终点.与此相反,一些注重提升学生数学素养的课堂,教师和学生并不以问题的解决为终点,而是对这个问题探索多种解法并在比较中对问题的解决方案进行优化.事实上,优化思维是提升学生数学核心素养的一种很好的方法.我们提出的理念是备课时要精选经典题,在课堂教学中要对经典题进行充分的发散研究,并且在发散研究的基础上比较研究,通过思维优化才能保质保量地提升学生的数学核心素养.以本题所述这道题的第(3)小题的教学为例,教学中要激发学生“一题多解”, 然后让学生在多个解答中对比,找到每种解法的优势与不足,找到自己思维的优势与不足,从而通过反思达到“思维优化”的目的.我们还主张对问题进行“变式”,然后引导学生对新的问题“一题多解”并重复上述过程.

4.3 鼓励学生追求“思维创新”

阅卷完返校之后,笔者访谈自己教过的学生对本题的答题情况,有一位学生根据等分点性质给出了一种创新解法.

解: 如图2,连接OP,OA,OB,

∵SΔAOP:SΔBOP=1:2,

∴AP:PB=1:2.

∵A(-1,4),B(4,-1),

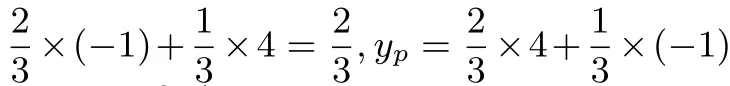
我对这位学生的这种解法很好奇,因为其思想很像“定比分点”公式,我问他是否自学了高中数学课程,他说没有.他告诉我, 他曾经研究过平面直角坐标系中线段的中点坐标公式的特点, 进而通过一些具体的坐标研究并得出了任意两点之间线段的n等分点坐标公式.他的研究结论是: 已知点A(a,b),B(c,d),若点C为线段AB的n等分点,且

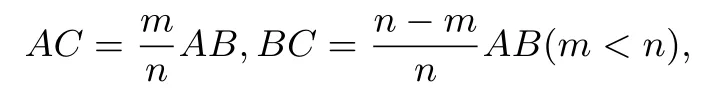
则

事实上,通过代入具体数据猜想并验证确实容易发现这个公式.据这位学生的学习经验,我们在教学中应该更多地为这类学生创造性学习提供资源和机会,鼓励他们追求思维创新.很明显,当学生能够习惯性地追求思维创新之后何愁其数学核心素养不强?

总之,我们在教学中要做的就是选出经典的问题,然后就是扎扎实实地引导学生实现“思维突破”, 激发学生坚持“思维优化”,鼓励学生追求“思维创新”.因为这些环节或方法才是提升学生数学核心素养的行之有效的好方法.