素养导向下高考导数解答题的备考之道—-2019 年高考全国Ⅰ卷第20 题的试题分析及备考启示

广东省佛山市南海区石门中学 刘伟

在2019 届高考备考中,笔者任教实验班,承担了学校尖子生培养的重任.高考备考中应如何突破导数解答题,一直是笔者教学及备考过程中不断思考的问题.本文中,笔者将结合对2019 年高考全国Ⅰ卷理科数学第20 题的研究,谈谈自己在导数题备考中的一些思考与体会.

1 试题呈现

已知函数f(x) = sinx-ln(1+x),f′(x)为f(x)的导数.证明：

(2)f(x)有且仅有2 个零点.

2 静观其“变”

该题的题干十分简洁,给出一个不带参数的函数解析式,题目设置两问,都是零点问题(第一问本质就是二阶导函数的f′′(x)变号零点问题).题干十分简洁,因为不带参数,给人的第一印象不会太难.但仔细一看,该题还是有很多“与众不同”的特点：

创新点1—-函数形式新：纵观近十年全国Ⅰ卷的导数题,基本都是由超越函数或与多项式函数的组合或复合而成的,几乎没有出现超越函数与正余弦函数组合而成的高考题,因此该题中出现的函数f(x)=sinx-ln(1+x)会让学生们感到十分陌生,不知如何下手.

创新点2—-考查方向新：2016 年起,广东省恢复使用全国1 卷的试题,2016 年及2018 年均考查了二元不等式,备考老师很容易形成一种备考的思维定势,过分关注二元不等式的相关问题,甚至把它放在导数备考中的首要地位,2019 年各地模拟题中层出不穷的二元(含x1,x2)不等式问题足以反映这种思维定势.此题考查的方向也与“预估”的不同,有较明显的反押题反刷题的味道,符合高考的公平性及选拔性要求.

创新点3—-设问形式新：本题两个小问均为证明题,这在近十年的全国卷中也是绝无仅有的.证明题是很多考生较薄弱的一种题型,该题设问形式的创新对考生来讲无疑是一种全新的挑战.

综上,这道题有诸多创新,必然成为学生通往高分路上的拦路虎!

3 素养导向

该题的命制符合高考评价体系中的“一核四层四翼”.从考查目的开看,该题能体现高考的选拔功能,也能很好地引导教学,引导中学数学教学回归到本质,即学科素养和关键能力的培养；从考查内容来看, 同时考查了四层即“必备知识、关键能力、学科素养、核心价值”；从考查要求来看,该题主要体现了高考的综合性和创新性.

证明定理是科研尤其是数学研究中最重要的工作之一,要求证明者具备较强的创新探索精神、分析推理能力及符号表达能力.本题设置两问,均为证明题,其用意是十分明显的——淡化对计算能力的考查,着重考查学生的分析能力和推理能力.因此,本题能力素养导向明显,考查学生分析问题、解决问题的能力,从数学学科核心素养来看,本题主要考查了逻辑推理、直观想象及数据分析三大核心素养.

4 试题分析

4.1 第一问

4.1.1审题分析

题干中出现了“极大值点”的关键词,不难想到该命题可化归为研究f′(x)的导数即f(x)的二阶导数f′′(x)的变号零点问题(由正到负),因此首先要正确求出f′′(x)；题干中的另一关键词“存在”,则意味着要从零点存在性定理入手,所以需要用到取点的技巧[1].“唯一”的证明则需要借助f′′(x)的单调性进行证明,所以在解决第一问的过程实际上需要求三阶导数f′′′(x).

4.1.2难点突破

(1)取点的“初体验”：在“唯一性”的证明中,涉及到取点分析的技巧,对于此类函数,应该取什么点?

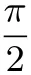
(2)借助高阶导函数解决问题时应注意什么?

笔者认为,函数题的作答用的是代数语言,但分析问题的过程中用得更多的却是“图像语言”.由于此题的证明过程中涉及到不同阶导数之间的联系,解题时需要借助各阶次导数的图象,画图分析的能力显得格外重要!一般的,解决函数问题的一个关键能力就是“画图”,借助函数图象可以打开解题思路,还能避免在抽象的代数分析中犯错.这是在平时教学中必须教会学生的一种关键能力,需要不断灌输,不断强化.以此题为例,借助几何画板可得f′(x)、f′′(x)、f′′′(x)的图象,可帮助直观理解问题：

图1 f′(x) = cos x-

图2 f′′(x) = -sin x+

图3 f′′′(x) = -cos x-

此外,从答题规范的角度来看,不建议考生在作答时使用高阶导数f′′(x)及f′′′(x)的符号,要求学生有清晰的思路和较强的符号表达能力.综上,第一问考查了求导运算,利用导数研究单调性,零点存在性定理等知识；考查了考生取点的技巧,本质是考查了数值分析的数学素养；考查了转化与化归及数形结合的数学思想.

4.2 第二问

4.2.1审题分析

第二问题干中的关键词是“有且仅有”,所以在证明的过程中就必须把2 个零点找到,而且还要证明不存在其他的零点.注意到第2 问与第1 问一个明显的差异是研究的范围变了,即在整个定义域而不是在一个有限的区间内研究零点的个数,而这是题目的困难之处!

4.2.2难点突破—-复杂问题的拆解

难点1：存在性—-“有2 个零点”如何证明?

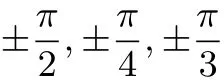
在存在性的证明过程中,我们可进一步体会到函数图象的重要性：任何函数难题的切入都应该把握函数的图象,应该借助函数的图象打开解题思路.函数f(x)在(0,π)的图象如下：

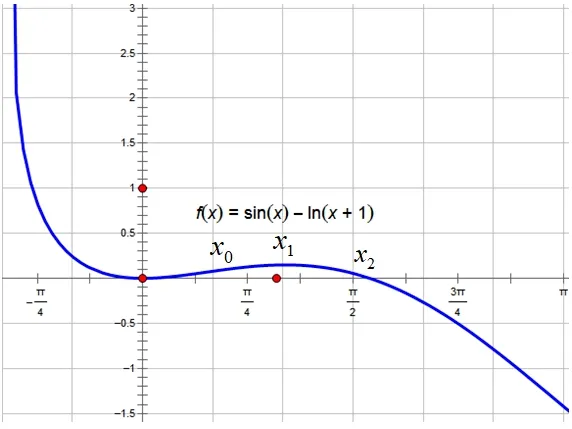
图4 f(x)在(0,π)的草图

思维误区分析很多考生会有这样的思维惯性,只要找到两个零点,再结合函数的单调性说明函数f(x)在零点x1,x2两侧是单调的就可以了,二次函数就是一个典型的例子.一旦进入这一思维误区,在第二问的证明中将会陷入一种困境：出现了单调性“解决不了”的问题!这是因为考生脑海中预期的理想模型图象如图5.

图5 思维误区中“理想模型”

事实上,单调性只是一个充分条件(条件太强),而不是充要条件,这就是该题的难点所在.

分析f(x)图象变化趋势的2 个角度：

(i)不难发现f(x)的零点即sinx= ln(1+x)图象交点的横坐标,结合这两个函数的图象,也不难发现第二个交点后f(x)的图象并非单调.

(ii) 事实上,f(x) 的图象在零点x2后有无限多个增减区间, 图象必然是“飘”的, 借助几何画板画出f(x) =sinx-ln(1+x)的图象,可验证我们的分析,但在考场上,学生要分析到这一点是非常不容易的.

图6 函数f(x)的图象

因此证明f(x)在(x2,+∞)内没有零点,利用单调性的思路是行不通的!这里需要另辟蹊径—-分段放缩法!

解题技巧2—-分段放缩法[1]由于正余弦函数是有界的,在含有sinx或cosx的超越函数的符号时,经常使用分段放缩法,这是处理这种形式的函数的一种通性通法.一方面,f(x)在(x2,π)上单调递减,从而f(x)＜0；另一方面,由sinx的有界性和-ln(1+x)的单调性得：

x ∈[π,+∞)时,

f(x)=sinx-ln(1+x)＜1-ln(1+π)＜1-ln 3＜0

注意到,这里依然需要使用到取点的技巧.至此,本题解题思路及方法分析到此结束.

4.3 详细解答

证明：(1)f(x)的定义域为(-1,+∞),

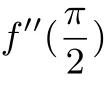
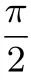
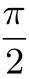
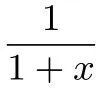
于是可得下表：

x (-1,0)0(0,x1)x1(x1, π π 2)(π π f′(x)-0+2 2,π)0----f(x)减函数0增函数大于0减函数大于0减函数小于0

综上,f(x)有且仅有2 个零点.

5 深度挖掘

5.1 命题者的意图

变式训练1：证明函数f(x) = sin-x2有且仅有2 个零点.

变式训练2：证明函数f(x) = sin-x3有且仅有3 个零点.

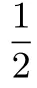
通过以上3 个变式练习的解决, 我们可以体会到变式1 与变式2 的解决方法与变式3 的差异：变式1 及变式2的证明方法是类似的,直接用单调性即可解决；变式3 则是f(x)=sinx-ln(1+x)的“降级处理”,证明方法相同,但难度略低.借助这3 个函数的图象,我们更能理解命题者的意图：为了使图象“飘起来”,需要恰当控制f(x)=sinx-g(x)中g(x)的增长速度!命题者选中增长较慢的ln(1+x)与具备无限多个增减区间的sinx组合,原因就在于此!

图7 变式1～3 的函数图象

5.2 寻根溯源

取点赋值技巧实际上是解决函数零点问题的一种常用技巧,在证明零点存在时最严谨的做法也是取点赋值(极限法并非最佳选择),在以往的高考题中不乏设计到取点技巧的题目.在此,仅列出两道高考题,作为横向比较：

题组1 涉及放缩及取点技巧的高考题

(1) (2015. 全国高考数学新课标卷(1) 文21) 设函数f(x)=e2x-alnx.

(i)讨论f′(x)零点的个数；

(2(2016. 全(1) 理21) 已知函数f(x) = (x -2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围；

再新的题目也有迹可循,今年全国一卷引入了含sinx的超越函数,是一种新的尝试.但此类函数题在其他省份的高考题也早已出现,解题时使用到的取点技巧和放缩技巧也早已出现在高考中,在此,列出几道旧题以备参考：

题组2 含sinx或cosx的超越函数的经典问题

(1)(2017 年北京理)已知函数f(x)=excosx-x.

(i)求曲线y=f(x)在点(0,f(0))处的切线方程；

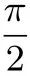
(2) (2017 年山东理) 已知函数f(x) =x2+2 cosx,g(x)=ex(cosx-sinx+2x-2),其中e ≈2.71828...是自然对数的底数.

(Ⅰ)求曲线y=f(x)在点(π,f(π))处的切线方程；

(Ⅱ)令h(x) =g(x)-af(x)(a ∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.

(3)(2014 年辽宁理)已知函数

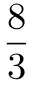
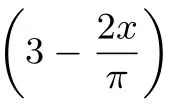
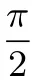
(3)(2013 年辽宁高考数学卷，理)已知函数

6 总结及反思

纵观整份2019 年高考数学试题(尤其是第4 题, 第21题,第22 题),有很浓的扭转应试教育的倾向,即反押题、反刷题,题目背景新颖,注重考查学生的核心素养和学科能力.试题充分体现了高考的公平性、选拔性,对中学的数学教学有很强的导向性—-素养培养比机械刷题更重要!笔者是十分欣赏今年的全国卷试题的, 也希望命题者能够扛住压力,继续命出如此高质量的好题!如此,才能更有利于高校选拔人才,更科学引导中学的课堂教学,回归到数学能力和素养的培养,而不是疯狂搞“题海战术”.如此,才是真正的利国利民,才能真正实现“减负”!

然而,导数题应如何备考?导数题的解题教学应该以什么为导向?教师应该注重教什么?成为我们必须要认真思考的一个问题!

笔者认为, 备考中让学生熟悉往年的高考题十分必要,但其目的不是押题.导数题备考的正确方向应该首先回归到关注学科研究的本质、关注考查的数学素养(如直观想象及数据分析的素养),关注考查的数学思想(如数形结合、转化与化归、分类讨论),其次才是处理问题的种种技巧.具体到函数与导数模块的备考,教学中应该教会学生：研究函数的问题要回归函数图象的变化,借助函数的图象打开解题思路,一切的解题技巧都只是由图象衍生出来的.而这才是真正的跳出题型看到问题的本质,这才是导数压轴题的备考之道!