例谈同源法构造函数在解题中的应用

安徽省芜湖市第一中学(241000) 刘海涛

在高中数学解题中,有些题中的等式(或不等式)经适当整理后,可以表示成两侧结构相同的形式,利用这个结构式构造对应函数,再用函数单调性解题的方法,我们通常叫做同源法构造函数.本文例谈同源法构造函数在高中数学解题中的应用,与读者分享.

1 同源法在解方程(或方程组)中的应用

例1解方程log13(5x+12x)=log5(13x−12x).

解析设log13(5x+12x)= log5(13x−12x)=t,则5x+12x= 13t,13x−12x= 5t,两式相加得5x+13x=5t+13t,构造函数f(x)= 5x+13x,有f(x)=f(t),易知f(x)为增函数,则x=t,于是5x+12x=13x,即易知函数为减函数,且g(2)=0,所以x=2.

点评本题设两个相等的对数值为t后,将对数式变形为两个指数和式,相加整理得5x+13x=5t+13t,等式两侧结构相同,于是应用同源法构造函数解题.

例2已知x,y ∈R,满足

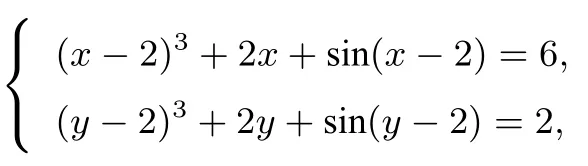
求x+y的值.

解析由题,方程组整理为

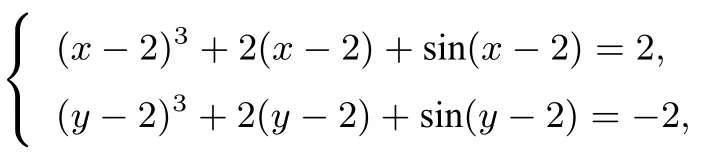
即

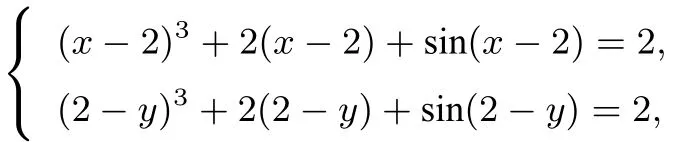
构造函数f(x)=x3+2x+sinx,有f(x −2)=f(2−y),由f′(x)= 3x2+2+cosx >0,得f(x)为增函数,所以x −2=2−y,即x+y=4.

点评解决本题的关键是弄清题目的研究对象是x −2和2−y,整理方程组出现(x −2)3+2(x −2)+sin(x −2)=(2−y)3+2(2−y)+sin(2−y),两侧结构相同,构造函数f(x)=x3+2x+sinx解题.

2 同源法在求解(或证明)不等式中的应用

例3若0

A.ex2−ex1>lnx2−lnx1B.ex2−ex1

C.x2ex1>x1ex2D.x2ex1

解析选项A、B 可分别变形为ex2−lnx2>ex1−lnx1、ex2−lnx2< ex1−lnx1,于是构造函数f(x)=ex−lnx(0g(x2),即故选C.

点评该题是典型的同源法构造函数解题,由选项A 和B 变形可构造函数f(x)=ex−lnx,由选项C 和D 变形可构造函数,接下来只需要判断构造函数在(0,1)上的单调性,再利用单调性判断不等关系即可.

例4若实数x,y满足3x+5y<3-y+5-x,则( ).

A.x+y >0 B.x+y <0 C.xy

解析由题,不等式整理得3x−5-x<3-y−5y,构造函数f(t)= 3t−5-t,有f(x)< f(−y),易知f(t)为增函数,则x<−y,即x+y <0,故选B.

点评解决本题的关键是将不等式中的变量x,y分离到不等号的两侧,出现3x−5-x<3-y−5y,两侧结构相同,于是构造函数f(t)=3t−5-t解题.

例5已知a > e,比较ea-1与ae-1的大小,并证明你的结论.

解析要比较ea-1与ae-1的大小,同取自然底数的对数,即比较(a −1)lne与(e −1)lna的大小,即比较与的大小,构造函数即比较f(e)与f(a)的大小,求导得设求导得当00,当x>1 时g′(x)<0,则函数g(x)在(0,1)上递增,(1,+∞)上递减,所以g(x)≤g(1)= 0,得f′(x)≤0,所以函数f(x)为减函数,故f(a)< f(e),即

点评解决该题的关键是用取自然对数的方法使得a与e两个量分开,得到与,自然考虑同源函数利用导数判断单调性后比较大小.

例6已知函数f(x)=aex−lnx −1.

(1)设x= 2 是f(x)的极值点,求a及f(x)的单调区间;

解析(1)在(0,2)单调递减,在(2,+∞)单调递增.(过程略)

点评首先将不等式f(x)≥0 放缩为ex-1−lnx−1 ≥0,接下来经过适当变形为xex≥ln(ex)·eln(ex),两边结构一样,构造函数g(x)=xex(x>0)解题.另外,此题也可将不等式变形为exlnex≥exln(ex),构造函数h(x)=xlnx来解题,或变形为lnx+x≥ln(ex)+ln(ln(ex)),构造函数ϕ(x)=x+lnx来解题.

3 同源法在求参数中的应用

例7已知函数且对于任意的若|f(x1)−f(x2)| <λ|x1−x2|恒成立,则λ的取值范围是____.

解析求导得f′(x)=cos 2x−cosx=2cos2x−cosx−1,当时易得f′(x)∈[0,2],则f′(x)≥0,所以函数f(x)在上递增,不妨设x1< x2,则f(x1)< f(x2),于是有f(x2)−f(x1)<λ(x2−x1),整理得f(x2)−λx2< f(x1)−λx1,构造函数g(x)=f(x)−λx,问题转化为函数g(x)在上递减,求导得g′(x)=f′(x)−λ,则g′(x)≤0 在上恒成立,即λ≥f′(x)在上恒成立,于是λ≥f′(x)max,故λ≥2.

点评利用函数f(x)的单调性将不等式|f(x1)−f(x2)| < λ|x1−x2|变 形 成f(x2)−λx2

例8设x>0,若aex−lnx+lna≥0 恒成立,则a的取值范围是____.

解析由aex−lnx+lna≥ 0 得则两边同取自然底数的对数,得,构造函数f(x)= lnx+x,即易知函数f(x)递增,则两边同取自然底数的指数,得即设函数求导得当0< x <1 时g′(x)>0,当x >1 时g′(x)<0,则函数g(x)在(0,1)上递增,(1,+∞)上递减,所以故

同源法构造函数是高中数学解题的一种常见方法,在解题中若能通过观察、分析、整理,使等式(或不等式)两侧同构,则可轻松构造函数,巧妙利用函数单调性解题.