多目标优化问题(C,ε)-近似解的一类组合标量化方法
刘佳星,张 琦
(重庆师范大学 数学科学学院,重庆 401331)
多目标优化理论与方法是数学规划中的重要分支,且在工程管理、航空航天、交通安全等诸多领域都具有十分广泛的应用.对于多目标优化问题的研究已有大量的研究成果[1-3],其中关于多目标优化问题解的定义是至关重要的.早期的研究主要集中于精确解的类型.而在实际的工作生产和生活实践中,多目标优化问题的(弱)有效解的集合可能是空集,但近似解在很弱的条件下都可能存在.因此,对于多目标优化问题近似解的研究是具有十分重要的理论价值和实际意义的.近年来,关于多目标优化问题近似解的相关研究已有大量的研究成果出现[4-6].特别地,Gutiérrez等[6]利用Co-radiant集定义了多目标优化问题的近似有效解和近似弱有效解,并说明了此(C,ε)-近似解包括了目前已知的许多ε-近似解的概念作为其特例.
对多目标优化问题进行标量化刻画是求解多目标优化问题时的一个重要途径.特别地,1983年Haimes[7-8]提出了著名的ε-约束法,并建立了多目标优化问题(弱)有效解的线性标量化结果.2008年Ehrgott和Ruzika[9]进一步对Haimes提出的标量化方法进行了改进,获得了有效解的线性标量化结果.
受文献[9-11]等研究工作的启发,本文利用改进的ε-约束法标量化模型进一步建立了多目标优化问题在Co-radiant集下的(C,ε)-有效解和(C,ε)-真有效解和E-近似解的一些标量化结果.
1 预备知识
假定R表示所有实数构成的集合,Rm表示m-维Euclid空间,0表示m-维零向量.本文考虑如下多目标优化问题:
(MOP) minf(x)=(f1(x),f2(x),…,fm(x)),
s.t.x∈X⊂Rn.
其中fi:X⊂Rn→R,X是(MOP)的非空可行集.对任意的1≤i≤m,fi(x)为有上界的函数,即存在Ui∈R使得fi(x)≤Ui.对于任意的y,z∈Rm,考虑如下的序关系:y 本文考虑如下的改进的ε-约束法标量化模型: s.t.fi(x)-si≤σi,i≠k, si≥0,i≠k, x∈X. 目标函数为第k个目标加上关于剩余变量si的权和,其中μi≥0,∀i≠k是剩余变量si的权重;当μi=0时,(SOP)退化为传统的ε-约束法. 利用改进的ε-约束法标量化模型(SOP)建立了(MOP)的(C,ε)-弱有效解、E-弱有效解、(C,ε)-有效解和E-有效解等系列近似解的标量化结果. 注在定理1中,Co-radiant集C的范围不能放松至C⊂Rp. 例1考虑如下的多目标优化问题:(MOP)f(x)=(f(x1),f(x2))=(x1,x2),s.t.x∈X={(x1,x2)∈R2|x1=0,-2≤x2≤0}.C={x∈R2|x1+x2≥1}.此时C为凸的Co-radiant集但C⊄RP+,取ε=1,μ=(0,1),s=(1,0),则有且所以是(SOP)的-最优解,但不是(MOP)关于C的ε-弱有效解. 例3考虑如下的多目标优化问题:(MOP)f(x)=(f(x1),f(x2))=(x1,x2),s.t.x∈X={(x1,x2)∈R2|x1+x2≥0,x1≤0,x2≤1}.C={x∈R2|x1+x2≥1;x1≥0;x2≥0}.令ε=1,μ=(1,1),s=(1,1),此时有且所以不仅是(SOP)的-最优解,还是(MOP)的(C,ε)-有效解. 注文献[9]在Euclid空间中对多目标优化问题的精确解(命题3.1-4.1、定理3.1-定理4.2)进行了标量化刻画,本文利用Co-radiant集和改进集中多目标优化问题近似解的定义,定理1-定理3对多目标优化问题(C,ε)-近似解进行了标量化刻画,推论1-推论2对多目标优化问题E-近似解进行了标量化刻画. 本文主要利用一类改进的ε-约束法标量化模型研究了多目标优化问题几类近似解的一些标量化性质,给出了近似解与标量化问题近似最优解之间的关系.关于多目标优化问题及其性质研究,特别是多目标优化问题的近似解及其线性与非线性标量化性质还有很多问题有待进一步深入研究.例如:目前已有的标量化模型与方法均含有大量的参数,这些参数如何进行有效确定是值得深入研究的问题;目前已有的各类标量化模型与方法中均含有大量的参数,如何提出新的标量化模型与方法、实现用较少的参数对多目标优化问题各类精确解或近似解进行等价刻画也是有待突破和解决的问题.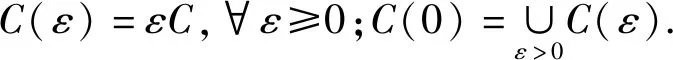
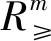

2 主要结果
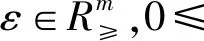
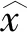
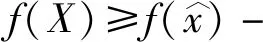

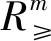
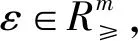
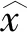

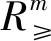

3 结语

