泰勒级数在高等数学中的应用研究

韩冰冰

（盘锦职业技术学院基础部，辽宁盘锦124000）

在高等数学中，泰勒级数属于函数项级数中幂级数的一种特例。泰勒级数作为一种数学工具，能够使数学问题变得简单，因此常应用在理论研究和数值计算中。由于泰勒级数的知识难度较大，为了让学生更好地掌握泰勒级数，有必要将泰勒级数知识进行详细论述，以提高学生的学习兴趣。本文将从泰勒级数的类型、展开条件、展开方法和应用出发，通过探讨合理地建立泰勒级数的教学体系，以提高学生学习效果。

1 泰勒级数的类型

1.1 一元函数y=f(x)的泰勒级数

如果函数f(x)在点x0处存在直至n阶的导数，那么x0的邻域内有n阶的泰勒级数[1]

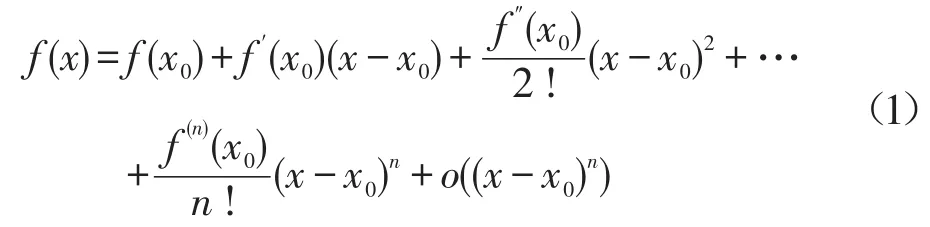
①f(x)在x0=0时，级数就是麦克劳林级数[2]，即

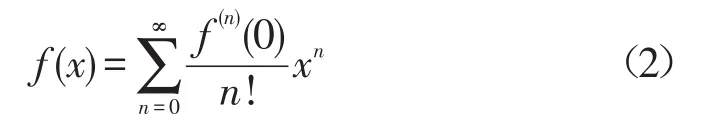
这种展开式是唯一的，而且函数f(x)的麦克劳林级数和x的幂级数是一致的。但是需要注意的是，如果f(x)在x0处有各阶导数，那么泰勒级数能否在某个区间内收敛，是否收敛于f(x)仍需验证[3]。

而泰勒级数收敛的充要条件是f(x)在x0处泰勒公式余项的极限为0，即如公式（3）[4]

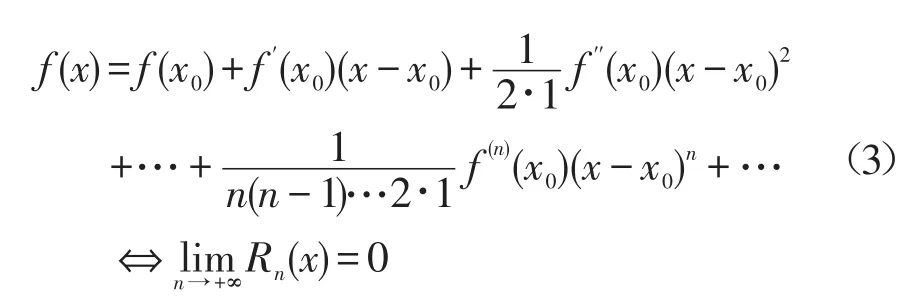
当f(x)的各阶导数都存在时，即泰勒级数在收敛情况下，与泰勒公式相同，都等于f(x)。

②f(x±a)在x处展开时的泰勒级数[2]为

1.2 多元函数y=f(x)的泰勒级数(以二元为例)

如果二元函数u=f(x,y)在点(x0,y0)对x及y具有直到n+1阶的连续偏导数[3]

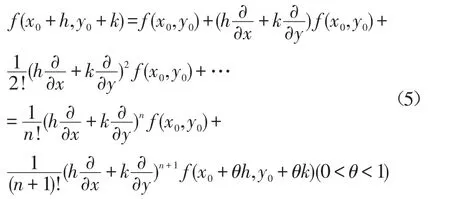
展开后就得到二元函数的泰勒级数。

下面以一元函数y=f(x)的泰勒级数为例进行说明。

2 泰勒级数的展开条件

不同函数在展开为泰勒级数时的条件是不同的。复函数f(z)展开条件比较简单的原因是有柯西积分公式及推广形式[5]

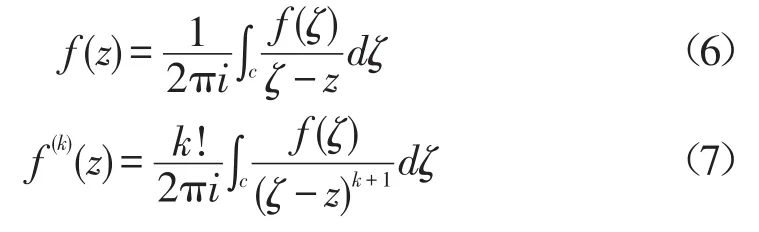
而实函数f(x)展开为泰勒级数条件很苛刻，必须具有如下条件[5]：

①f(x)在x0点存在各阶导数；

②存在δ＞0，使一切x，只要|x-x0|＜δ，便有

其中，rn为泰勒级数的余项。

所以，在解决实函数f(x)时，可以通过复函数f(z)进行求解。

3 泰勒级数的展开方法

把函数展开成泰勒级数，主要有直接展开法和间接展开法。

3.1 直接展开法[6]

直接展开法主要分为四个步骤进行：

①求出函数的各阶导数f(x),f'(x),…,f(n)(x),…;

②函数f(x)及各阶导数在x=x0处的值：f(x0),f'(x0),…,f(n)(x0),…;

③写出泰勒级数

④考察余项Rn(x)在x0的某一邻域U(x0)内的极限是否为零。

3.2 间接展开法

由于直接展开法的展开过程比较烦琐，实际应用较少。所以泰勒级数在展开时，常用间接展开法[7]。下面就利用间接展开法来简单介绍泰勒级数的应用。

3.2.1 函数的近似计算[8]

3.2.2 证明不等式

例2设n为自然数，试证：（当t≤n时）

证明：不等式两边同乘e-t，利用麦克劳林级数展开，则

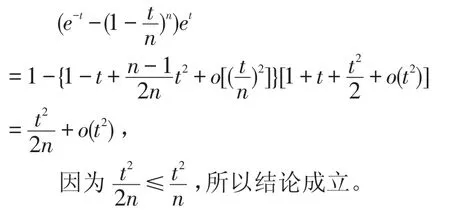
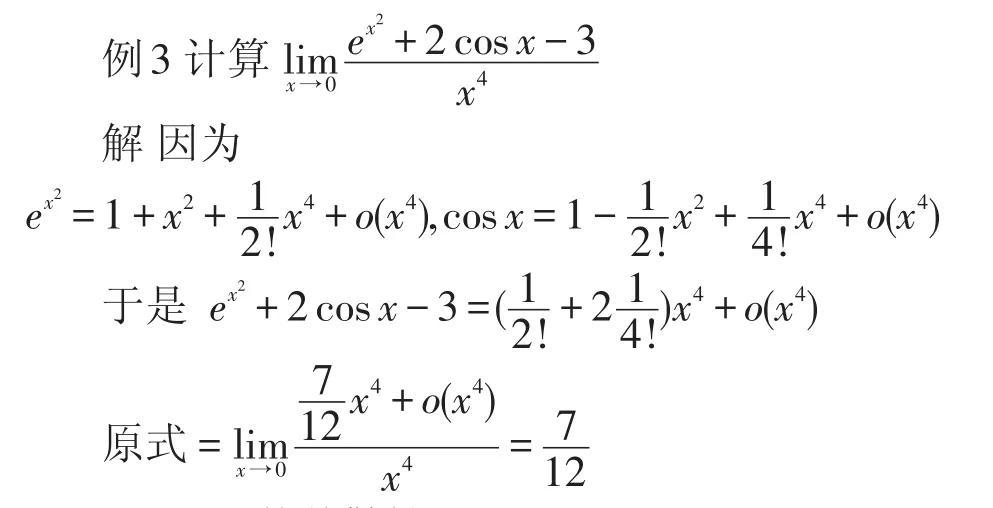
3.2.3 函数极限[4]3.2.4级数敛散性[9]