汽车总装线配置的优化模型研究

董 慧，唐云芳

（安徽工业经济职业技术学院，合肥230001；中国计量大学，杭州310018）

1 问题提出

汽车装配中，由于受生产工艺、质量控制及成本等因素影响，总装线的配置要求多且复杂，合理安排装配顺序对保证汽车装配效率及质量，提高竞争力有着重要的意义。结合这一实际，2018年全国大学生数学建模竞赛D题探讨了如何优化汽车总装线的配置以实现生产均衡化，即在各装配要求的约束下给出符合要求且具有较低生产成本的装配顺序[1]。具体要求可以参见全国大学生数学建模竞赛官网。

2 问题分析

汽车装配过程中既要保证生产质量，提高装配效率，又要尽量降低成本，实际上就是要实现生产的均衡化、平衡化，属于最优化问题，因而将配置要求量化构建优化模型即可实现。

汽车在装配时主要对确定汽车型号的五种属性做了详细的装配要求，这五种属性分别是品牌、配置、动力、驱动及颜色，其中前四种属性的要求较少且简单，颜色的要求较复杂，因而我们可以将品牌、配置、动力、驱动作为模块1，颜色作为模块2，通过量化装配要求构造出约束条件及目标函数，从而建立出各模块的优化模型。最后，将各模块的模型综合起来得出符合要求且具有较低生产成本的装配顺序[1]的优化模型，通过遗传算法求解出模型。

3 问题假设

①假设汽车装配过程中不会出现任何故障，装配计划不会临时调整。

②同一种油漆喷涂时间过长时，不考虑胶结凝聚现象。

③假设喷漆过程不会出现施工质量问题。

4 模型建立与求解

每天白班和晚班装配任务一样，在此我们只讨论白班的装配顺序。若汽车总数为偶数，晚班按同样的装配顺序，若为奇数，则白班多装配一辆，晚班少一辆，通过适当调整可得到。

4.1 按装配要求划分模块

经分析，我们将品牌、配置、动力及驱动作为模块1，颜色作为模块2，分别构建模型。模块1中，结合数据发现，品牌、动力、驱动、配置的要求复杂度依次增高，根据复杂度设置各因素讨论的优先级，具体划分如图1所示。

图1 模块划分图

4.2 模块1的数学模型

每班次都是按先A1后A2的品牌顺序进行装配，而每种品牌里其他因素的要求都一样，以下我们仅讨论白班中A1品牌汽车的装配顺序，其他情况讨论方法一样。

按动力划分时，柴油汽车相比汽油汽车，数量非常少，可先装配汽油汽车，再根据柴油的装配要求简单排序即可。假设A1品牌汽车有N辆，其中四驱汽车n辆，为方便讨论，我们将总装线按顺序标号，即标注1,2,...,N。下面我们根据驱动和配置的要求分别构建模型。

4.2.1 根据驱动构建模型

由于四驱汽车最多连续装配两辆，为降低成本，我们按最大连续装配允许量两辆讨论，所以四驱汽车应连续装配n/2批，夹在两批四驱汽车之间装配的两驱汽车为n/2-1组，令第i组两驱汽车的数量为wi，根据要求应满足下列条件：

③每组两驱汽车的数量应尽量均衡，在此，我们引入均衡度α的概念，记,α越小说明每组的数量越均衡。

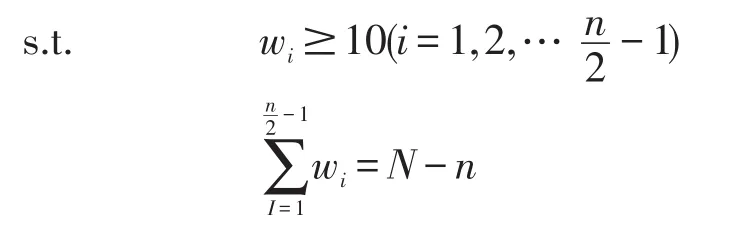
4.2.2 构建配置连续数量最大化模型

令白班中A1品牌中配置为Bm的车共有dm(m=1,2,… 6 辆，

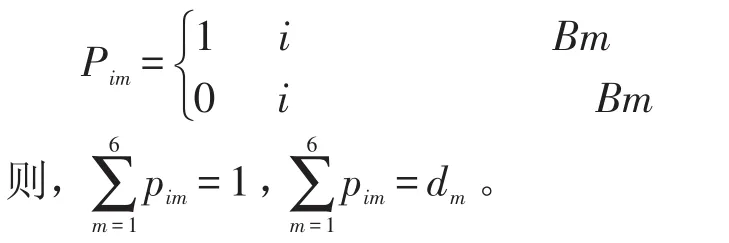
由于相同配置车辆应尽量连续装配，故以配置连续数量最大为目标函数构建模型如下：

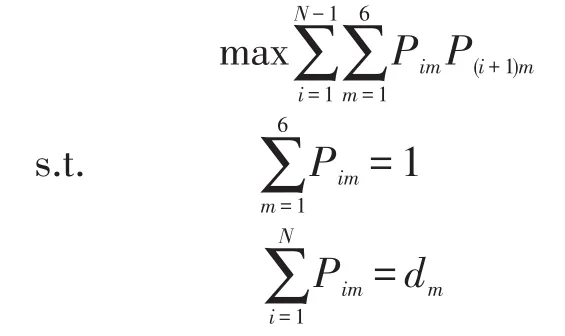
4.2.3 模块1的优化数学模型

根据构建的模型，我们得出优化模型Ⅰ

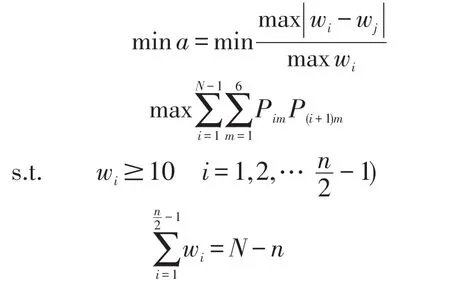
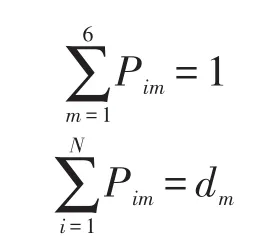
4.3 模块2的数学模型

汽车进行喷涂作业时需按序依次在C1,C2线上交替进行，即总装线上奇数位的汽车在C1线上喷涂，偶数位的汽车在C2线上喷涂。为构建模型，我们对颜色的要求进行量化处理。

1.3.1 颜色编号

我们将9种颜色依次编号，见表1。

4.3.2 符号假设

为构建模型，引入下列记号：

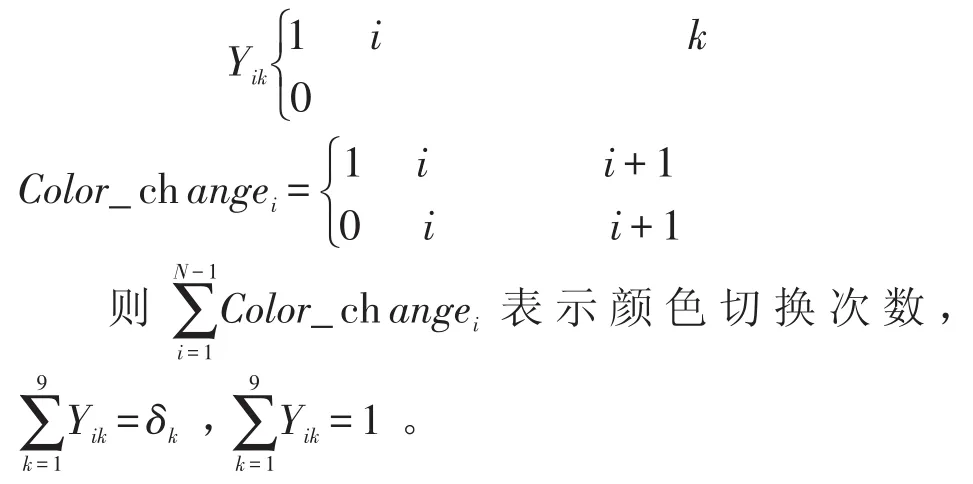
4.3.3 约束条件

①当汽车为蓝、黄、红三种颜色时只能在C1线上进行喷涂，即偶数位未被涂成蓝、黄、红，则需满足，当k=3、4、5 时，Y2m,k=0 。

②当汽车为金色时只能在C2线上进行喷涂，即奇数位未被涂成金色，故Y(2m+1)8=0。

③对于总装线上要求可连续排列的颜色，假设第k1、k2种颜色可连续排列，则这两种颜色所在位置的序号差应为1，

④对于总装线上要求必须间隔排列的颜色，假设第k1、k2种颜色必须间隔排列，则这两种颜色所在位置的序号差应为2，故应满足

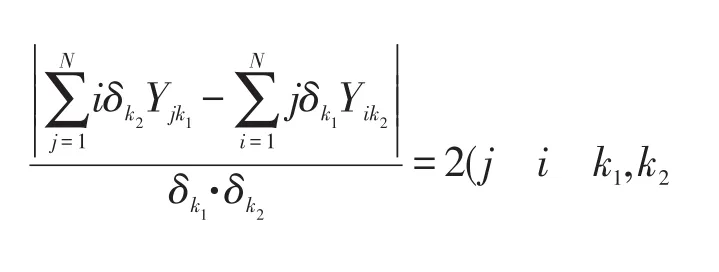
⑤颜色切换应满足

⑥同种颜色的汽车连续喷涂的最大量应不大于该种颜色汽车的数量，故要满足

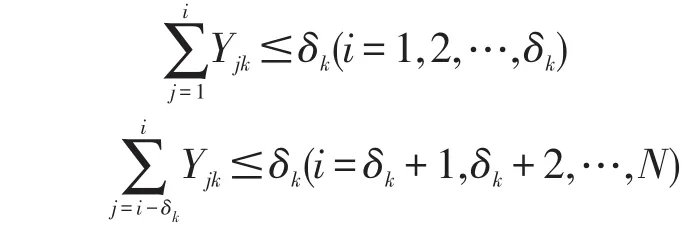
⑧当汽车为黑色时，它与其他颜色汽车在喷涂线上切换所造成的代价非常高，为降低生产成本，喷涂时黑色汽车应避免和其他颜色汽车切换，故应安排在装配线的最前方。

4.3.4 目标函数

5 模块2的数学优化模型

综上，我们得到优化模型Ⅱ

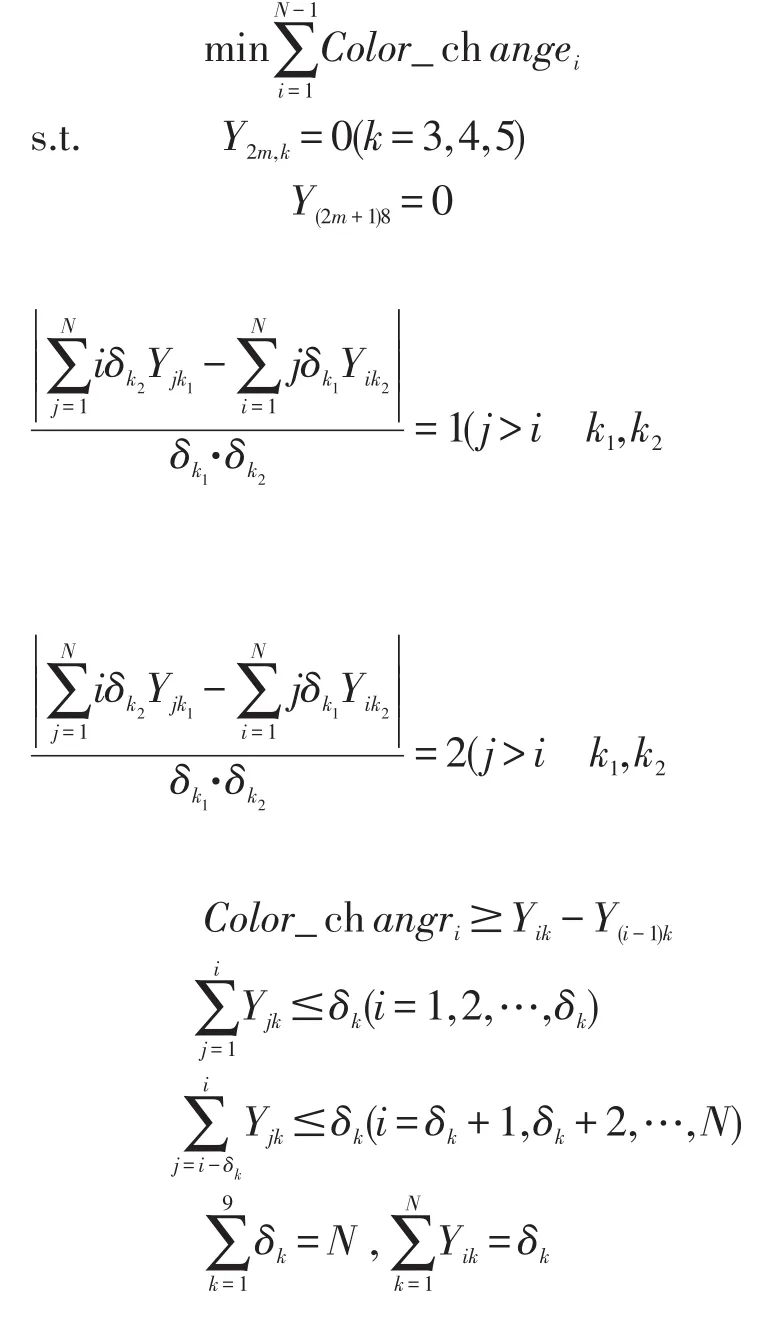
4.4 汽车总装线配置的优化模型

根据构建的Ⅰ、Ⅱ优化模型，我们得出问题的模型Ⅲ：

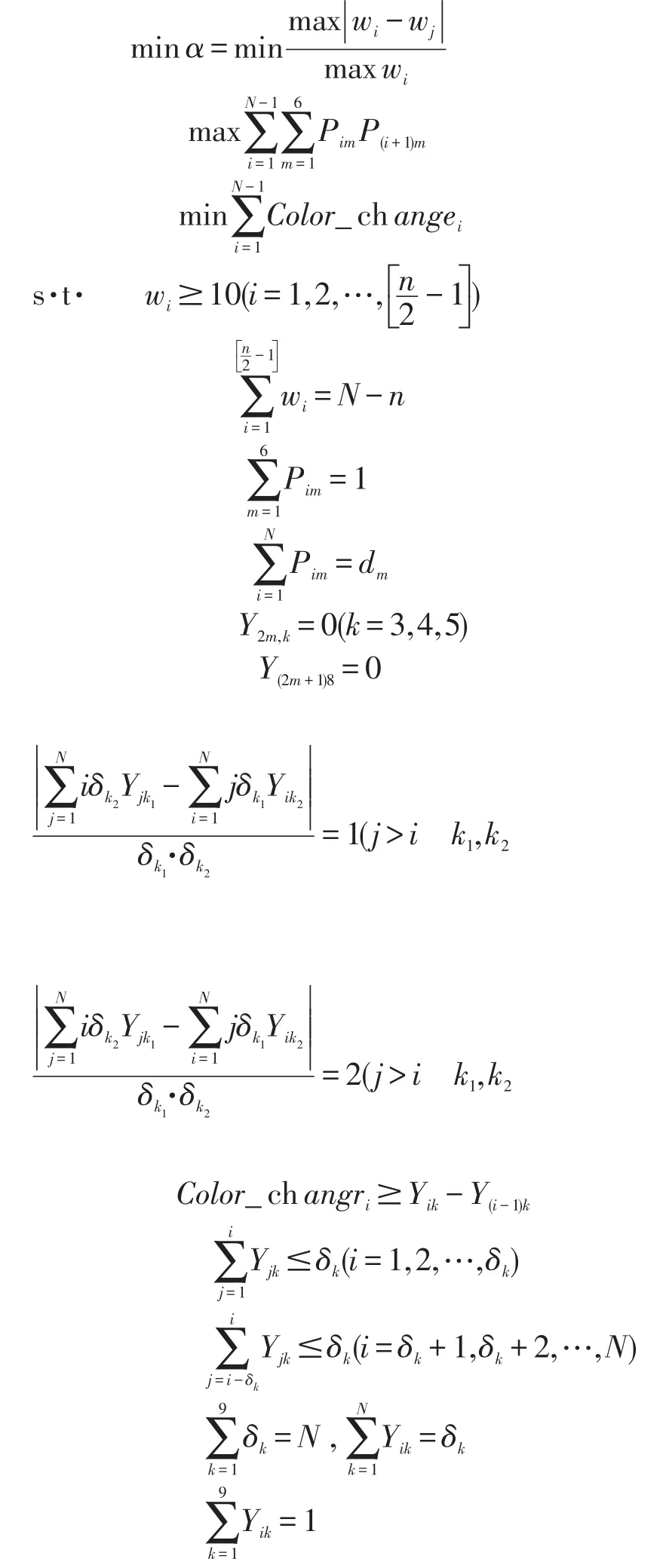
4.5 遗传算法求解模型

模型Ⅲ为优化模型，求解数据较大，可以用遗传算法来求解。遗传算法的基本操作流程简单明晰，具体操作如图2所示。

以9月20日为例，品牌A1里无柴油汽车，即柴油汽车的数量取值为0，代入数值利用遗传算法可求得。在此，列举前20位的装配顺序，见表2。

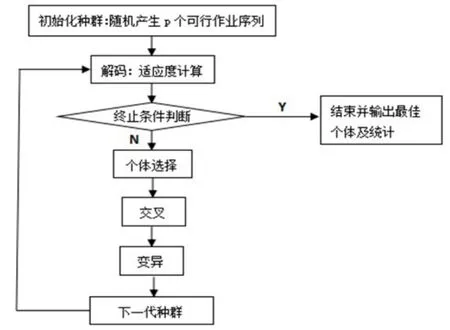
图2 遗传算法流程图

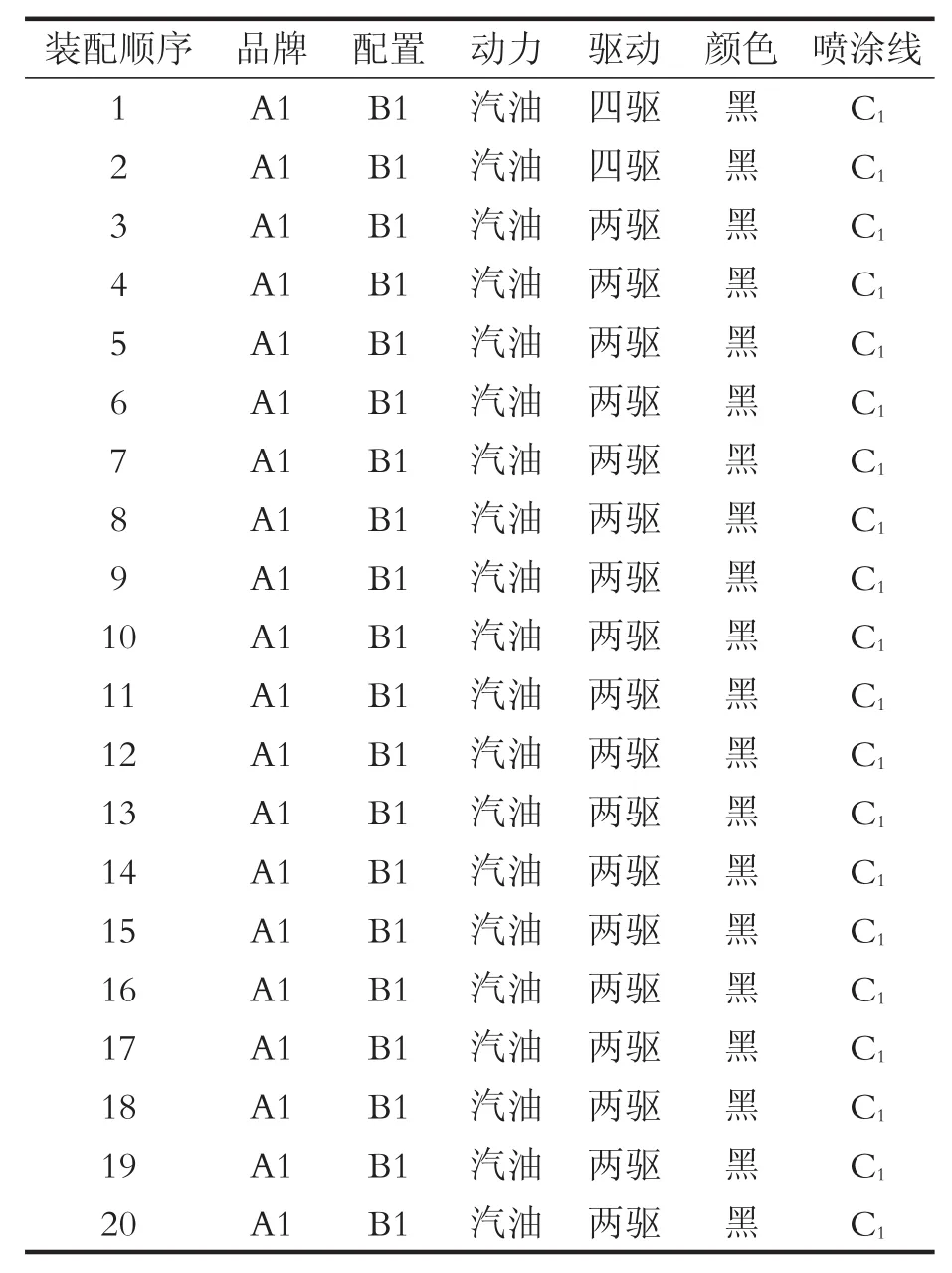
表2 9月20日装配顺序

5 模型评价

本文通过对各个约束条件的严谨分析，得出了较好的模型，思路清晰，结构严谨。但目标函数有三个且约束条件较多，求解较复杂，在一定程度上也影响到模型求解的精确度，后续仍要进一步优化。