融合白质功能信号的DWI纤维优化重建

肖 丹， 杨智鹏， 吴 锡， 周激流

(1.成都信息工程大学计算机学院， 成都 610225； 2.成都信息工程大学电子工程学院， 成都 610225；3.四川大学计算机学院， 成都 610065)

1 引 言

弥散加权成像(Diffusion Weighted MRI，DWI)是一种能够在大脑白质内检测出水分子弥散运动的无创方法.通过估计体素中水分子的弥散方向分布函数(diffusion Orientation Distribution Functions， dODFs)来间接计算白质纤维的分布方向[1].DWI纤维束追踪成像就是将dODFs转换成纤维方向分布函数(fiber Orientation Distribution Functions，fODFs)，并通过其在体素间的连通性来构建脑白质连接的解剖结构.研究脑白质神经纤维的组织特性,能够了解到大脑的发育、衰老和患病情况[2].

现有的DWI纤维重建算法可分为局部纤维重建方法和全局纤维重建方法.局部纤维重建方法是从初始点开始，沿着纤维走向逐步前进，最终获得整条纤维路径；全局纤维重建方法则是在互相连接的纤维路径上建立代价函数，利用优化技术寻找最佳纤维路径.全局纤维重建方法可以消除累积噪声及局部随机噪声，提高长距离成像的可靠性.

全局纤维重建方法中，目前常用的是在全局概率追踪的贝叶斯算法中加入先验信息，从而在两个区域之间找到最优纤维束的方法[3]，用类似大脑几何形状的模拟DWI作为可靠性估计进行定量评估[4].这种方法的缺陷在于可供使用的先验知识只包含了两区域间是否存在连接的信息，并不包括关于纤维束位置或功能的先验信息.此外，由于问题过于复杂，很难求出最优解，此方法只能通过从后验分布的启发式采样来估量纤维束.2012年，Wu提出了一种将全局纤维追踪与分层纤维聚类相结合的划分纤维路径的方法.这种方法采用了K均值聚类和改进的休伯特统计，在每个纤维束上进行迭代采样和聚类来逼近最优解，极大地促进了纤维束成像在人类复杂神经网络的临床研究[5].Eleftherios等人在进行白质纤维虚拟解剖研究时，采用了基于纤维流线的纤维束标记及聚类技术，将纤维束模型作为先验知识，检测出纤维束线图中更为精准的相似流线和束[6].由此可见，评价方程的计算作为全局优化类方法的核心，决定了优化后的结构连接是否符合真实生理结构.

重建具有功能意义的结构连接是神经科学研究中基础性的问题，以往的研究将DWI的结构连接与基于灰质中功能磁共振成像相结合，重建出连通多个灰质功能区域的白质结构连接.但目前的这些融合研究只是一种基本的联合，结果只能说明在特定的灰质功能区有白质纤维连接，白质结构本身并未证明具有功能特性.最新的研究表明，白质中的功能磁共振成像(fMRI)能通过测量白质神经元功能活动中的血氧依赖水平(Blood Oxygen Level Dependent, BOLD)来分析神经纤维的功能特性，并已成功应用于病理学研究，该研究为重建具有功能特性的纤维束提供了可能[7-8].

综上所述，本研究提出将白质fMRI融合到DWI全局优化纤维重建中，加入功能先验信息纤维重建出最优功能路径.该方法基于全局优化类的贝叶斯最优路径算法，从全局纤维中找到连接特定功能区域的最优路径，对数据进行初始化.其可有效抑制局部噪声，得到执行特定功能的最优连接路径，避免得到局部最优解.较之现有方法，打破了仅通过空间位置形成最优路径的框架，重建出在执行特定脑活动时，大脑信息传递的最优路径.

2 方 法

2.1 DWI优化方法

大脑的DWI数据定义为连接图G=(V,E,wE)，其中，V是除去脑脊液(CSF)以外的所有体素节点集，E是边集，wE是边的权重.在三维图像中每个节点都能被边e∈E连接到其3×3×3邻域中，并给每条边e赋予一个权重wE(e)∈[0,1]，用于表示纤维束连接其两个端节点的概率.路径的似然值是路径上所有的边权重wE(e)的乘积，即：

(1)

式(1)中，v∈V和v′∈V是G中的两个节点，πv,v′是连接这两点的路径，可表示成节点序列πv,v′=[v1,v2,...,vn]，其中，v1=v,vn=v′,(vi,vi+1)∈E,i=1,...,n-1.路径的基数等于其节点总数|πv,v′|=n.

我们用单位球面S2上的任意方向θ的fODFf:S2→R+求出纤维在该方向的概率，从而表示DWI的弥散情况.对每个体素的26个相邻体素方向θi,i=1,...,26进行研究.通过计算在所有方向集Ci的fODF，得到体素在方向θi∈S2上的权重w(θi)[9].权重w(θi)表示体素连接该方向的概率，可近似表示为

(2)

wE(v,v′)=1/2·(w(v→v′)+w(v′→v))

(3)

其中，v→v′表示从体素v到体素v′的方向，于是得到对称边权重：wE(v,v′)=wE(v′,v).

2.2 大脑白质fMRI信号建模

用DWI中fMRI相关张量来重建人脑中的功能结构，通过BOLD信号的时间波动来反映自发神经活动以及功能刺激下的诱发反应.对于BOLD数据集中的每个体素，可以构造时空相关张量以表征体素与其邻域之间的时间相关性的局部分布[10].

假设F是要构建的空间相关张量，估计的相关系数D沿单位向量ni(xi,yi,zi)投影得到

(4)

其中，t表示转置操作.

D=(D1,D2,...,D26)t表示沿着26个方向观察到的时间相关性的集合，FD是F重新排列后形成的列向量，则D和FD之间的关系可以表示为

D=M·FD

(5)

FD=(Mt·M)-1·Mt·D

(6)

其中，-1表示逆矩阵.

相关张量F(对应于最大特征值的特征向量)的主特征向量表示时间相关性的主要方向.本文假定该方向是局部小邻域窗口内的神经活动传播的方向.pF是功能ODF，它由吉布斯分布建模计算得到[11].该模型假定体素X中张量F仅取决于局部主方向VF(X).pF则可用以下公式表示.

(7)

其中，ZF是标准化常数.

(8)

方程中的势函数p随着函数方向VF(X)和最大张量特征值λ1之间的差异而减小.分母用张量范数进行归一化[12].对于各向异性张量，势能给出的概率分布集中在张量F的主特征向量的方向上.对于各向同性张量，势能函数将形成更宽的概率分布.

2.3 融合fMRI的DWI纤维优化重建

对于DWI图像中每个节点v∈V，pF(v)∈[0,1]表示该节点位于路径中的功能先验概率，使其在执行特定脑活动时，能根据功能信息形成大脑信息传递的最优路径.本实验提出一种有效的算法，即将脑图G=(V,E,wE)中沿边缘连接的贝叶斯模型，与表示节点功能信息的pF:V→+相结合. 边缘连接的贝叶斯模型可通过之前的节点和边e∈E的转化来构建.对于单边e=(v,v′)∈E，路径的功能先验概率P(e)定义为纤维束在v点处的功能概率pF(v)与v′点处的功能概率pF(v′)乘积的平方根.

(9)

给图像中每条边分配一个边缘权重wE(e)，用于表示大脑沿边e的结构连通性. 将公式(3)中的边缘概率wE用概率密度函数fe来表征.

(10)

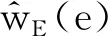
P(e|wE(e))∝P(wE(e)|e)P(e)=wE(e)P(e)

(11)

对于任意边e(v,v′)，有

-log(wE(e)P(e))=

(12)

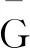
(13)

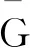
(14)

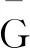
argmaxπv,v′P(πv,v′|G)

(15)

在以往的方法中，上式中路径概率是体素在这条路径上先验信息的乘积[13].这种方法的局限性在于，只能使用特定且有限的解剖先验信息(区域标签).

而本文提出的方法对边缘先验进行了重新定义，得到图像中可能存在的所有路径，通过修改图中的先验信息来直接求出纤维束成像的最优路径，并不需要从后验分布来进行路径采样.这种方法提供了大量的最优路径求解衍生算法，大大简化了计算量.

WM中的ODF的例子如图1所示.其中,P(πv,v′|G)是后验ODF(c)，从DWI计算的ODF(b)和相关张量的ODF(a)计算得到，用于表示体素内的功能通路方向.

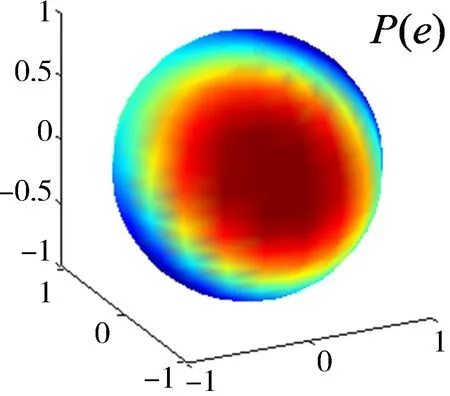
(a)

(b)

(c)

图1 单个像素功能路径方向的后验ODF

(a)功能ODF；(b)弥散ODF；(c)后验ODF

Fig.1 Posterior ODF of functional pathway directions for a voxel

(a) Function ODF; (b) Diffusion ODF; (c) Posterior ODF

3 实验结果

3.1 数据采集

全脑MRI数据来自健康的成年志愿者.实验仪器使用3T Philips Achieva scanner (Philips Healthcare, Inc., Best, Netherlands)，32通路头部线圈.实验数据集为四位成年人在进行感觉刺激实验时的触觉刺激功能图像.感觉刺激被设计为方波形式，刷子刺激手掌30 s然后无刺激30 s，周期重复.

采集参数：T2*-weighted (T2* w) gradient echo (GE), echo planar imaging (EPI) 序列采集了三组BOLD信号：TR=3 s、TE=45 ms、matrix size=80×80、FOV=240×240 mm2、34层和3 mm 层厚、145 volumes、435 s.同时利用a single-shot, spin echo EPI序列采集了diffusion weighted images (DWI) 数据：b=1000 s/mm2、32 diffusion-sensitizing directions、TR=8.5 s、 TE=65 ms、SENSE factor=3、matrix size=128×128、FOV=256×256、68 层和2 mm层厚.为提供解剖学依据，所有例均采集3D高分辨T1-weighted (T1w) 解剖结构图像，利用multi-shot 3D GE序列采集，像素大小1×1×1 mm3.

3.2 数据预处理

采集的数据均使用SPM12工具箱进行预处理.BOLD信号依次经过时间层矫正、头动矫正、FWHM=4 mm高斯平滑.如果头动位移超过2 mm以下、旋转大于2°，数据将被剔除.以b=0的DWI数据为参考， 将所有被试者的平滑后的数据配准到各自的DWI数据空间.T1w数据进行偏移矫正和分割得到白质、灰质和脑脊液，然后共同以b=0 DWI为参考配准到DWI图像空间.

3.3 优化重建实验

本研究分析了人脑临床数据的两个白质区域：丘脑至机体感觉区域和丘脑至岛叶区域.

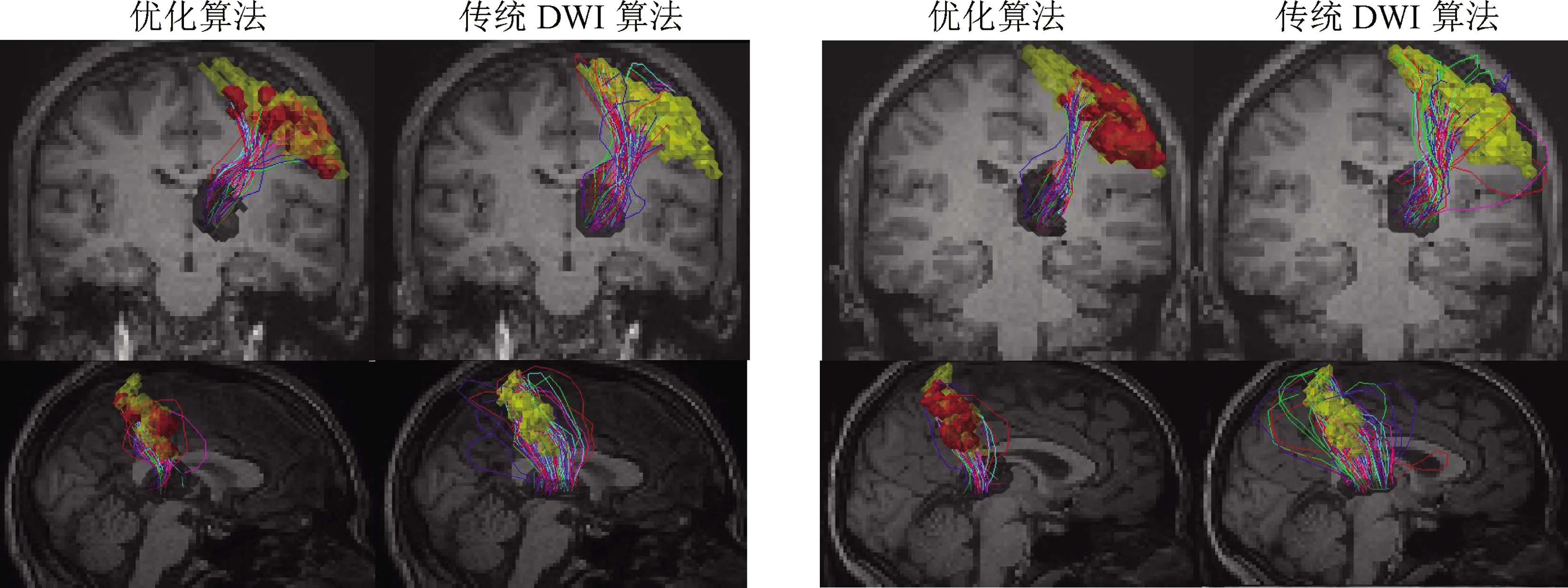
图2展示了从丘脑至机体感觉区域的跟踪结果，图中红色标记部分为大脑中央后回区域，从生理学分析，大脑中央后回接受背侧丘脑腹后核传来的对侧躯干四肢的痛、温、触压觉及位置和运动觉，在刺激实验者手掌时处于激活状态.

如图2所示，采用传统DWI算法得到了图中黄色所示的大面积皮层区域的通路，而融合白质功能信号的优化算法则能直接找到功能激活区域的通路.说明本实验优化算法能够重建执行特定脑活动时功能激活的白质纤维通路.如图3所示，优化算法相较于传统DWI算法，其概率密度更集中.

本文定义真阳性值(TP)来反映高概率区域中包含多少体素，从而对两种方法进行定量比较：

(16)

表1展示了传统DWI方法和本文优化算法的真阳性平均值和标准差，由表可知，优化算法相较于传统DWI算法，其真阳性参数平均值更大，方差更小.由此可知，本实验优化算法重建功能激活状态的通路时，获得纤维束更集中紧凑，较之现有方法具有更强的鲁棒性.

表1 丘脑至机体感觉区域真阳性平均值和标准差

Tab.1 Mean and standard deviation of true positive scores from thalamus to sensory area

算法真阳性平均值和标准差传统DWI0.073 2±0.026 优化算法0.283 5±0.011

(a) (b)

(c) (d)

图2 丘脑至机体感觉区域的跟踪结果

(a)～(d)分别为4个例子，其中每一例的第一排是冠状面视角，第二排为矢状面视角；灰色区域为种子点区域，黄色区域为传统DWI得到的大脑皮层区域，红色区域为触觉刺激激活的皮层区域(为方便观察流线，随机选择颜色进行展示)

Fig.2 Results of tracking from the thalamus to sensory area

There are 4 examples which the seed area are in gray color. The target ROI of traditional DWI method is in yellow color and activation area is in red. For each subject, the upper rows a coronal view and lower row is an sagittal view. Note that the streamlines are randomly colored for visual effect.

图3 丘脑至机体感觉区域的概率密度图

(a)～(d)分别为4个例子，其中每例第一排是为冠状面视角，第二排为矢状面视角；其中，黄色为高密度区域.

Fig.3 Probability density map from the thalamus to sensory area

There are 4 examples which the mean path directions with high probability in yellow color.

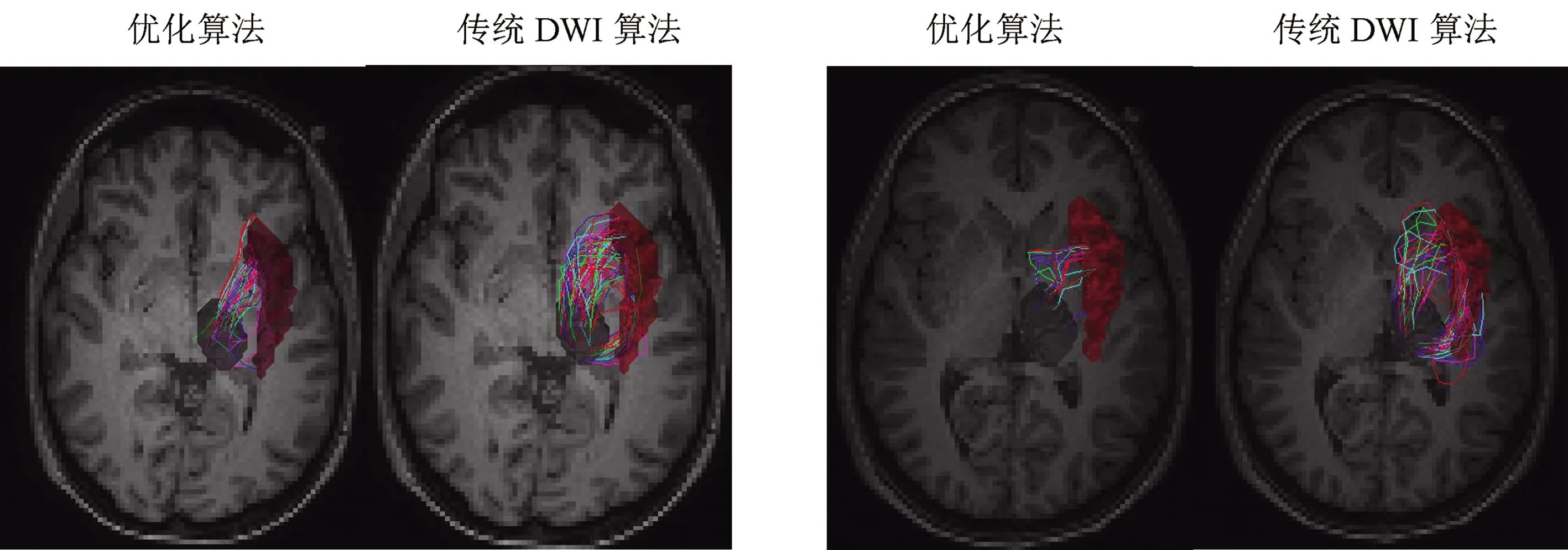
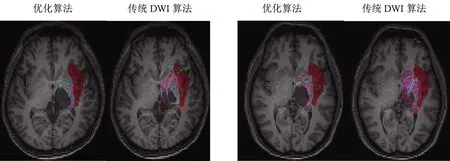
本实验还重建了被实验者受到手掌刺激时丘脑到岛叶的流线.文献[14-15]发现岛叶前部与丘脑有神经相连，并且该路径与触觉表达相关.由图4可知，在重建丘脑与岛叶区域的通路时，由于该区域白质纤维流向复杂，传统DWI算法用更多的追踪次数重建出来的纤维束更为分散，可靠性降低.而融合白质功能信号的优化算法用较少的纤维束追踪次数直接重建出岛叶前半部分的通路.

由图5和表2也可知，优化算法的实验结果更集中紧凑.

表2 丘脑至岛叶区域真阳性平均值和标准差

Tab.2 Mean and standard deviation of true positive scores from thalamus to insula

算法真阳性平均值和标准差传统DWI0.105 4±0.057 优化算法0.251 1±0.014

(a) (b)

(c) (d)

图4 丘脑至岛叶区域的跟踪结果

(a)～(d)分别为4个例子的剖面视角；灰色区域为种子点区域，红色区域为目标ROI区域(为方便观察流线，随机选择颜色进行展示)

Fig.4 Results of tracking from the thalamus to insula

The seed area is in red color and the target ROI is in gray color. There are axial views. Note that the streamlines are randomly colored for visual effect.

(a) (b)

(c) (d)

图5 丘脑至岛叶区域的概率密度图

(a)～(d)分别为4个例子的剖面视角；其中，黄色为高密度区域

Fig.5 Probability density map from the thalamus to insula

There are 4 examples which the mean path directions with high probability in yellow color.

4 结 论

本文阐述了弥散磁共振纤维跟踪重建可以融合白质fMRI信号的功能信息，用于跟踪特定神经活动状态下的功能活动通路. 时空相关张量对白质纤维沿线的功能特性建模，为基于DWI跟踪流程的跟踪方向提供有效的补充信息.此优化重建方法是研究人脑的结构功能相互关系的有用补充.

首先，本研究分析了连接丘脑和机体感觉区域的纤维束通路.中央后回接受背侧丘脑腹后核传来的对侧躯干四肢的痛、温、触压觉及位置和运动觉，在刺激实验者手掌时处于激活状态.传统DWI算法无法精准地找到功能激活状态的通路，而本研究优化方法能精准有效地找到了白质纤维束的功能活性通路，说明了本研究有助于解决白质功能结构跟踪困难的问题.

接着，本研究还分析了连接丘脑和岛叶皮层的纤维束通路.岛叶皮层与多种脑功能相关，如感知、运动控制、自我意识，认知功能和个体经验.脑岛的前部接收来自丘脑腹侧内侧核基部的直接信息.这条路径穿过复杂区域与其他功能路径交叉，基于DWI的跟踪重建在经过大量的跟踪次数后才能找到其通路，实验结果繁多且分散.相反，本文优化方法可以联合丘脑和脑岛之间的功能信息重建这条路径，重建结果集中且紧凑.实验结果表明本文优化方法具有研究岛叶皮层功能结构以及与其他区域连接的潜力.

综上所述，本研究提出了一种新的白质纤维束优化重建方法，它基于全局优化类的贝叶斯最优路径算法，利用白质中的功能信息来找到在执行特定脑活动时，大脑信息传递的最优路径.白质中fMRI信号的各向异性被建模为时空相关张量，并调制用于跟踪的弥散信号导出的ODF.本文融合白质功能信号的DWI纤维优化重建具有在特定功能回路中重建纤维通路的巨大潜力.