基于数学核心素养视角下的立体几何解法赏析
唐敏 严忠权


【摘要】2019年全国高考Ⅲ卷文科数学第19题通过对图形的翻折问题,考查四点共面、面面垂直的判定、求平行四边形面积,着重考查了立体几何中的点,线面位置关系的判断及证明,突出对学生分析问题、解决问题、空间想象能力的考查,此题推理论证及求解过程中体现出数学核心素养的直观想象、逻辑推理、数学运算[1].
【关键词】高考数学;核心素养;立体几何;解法探究
一、试题呈现
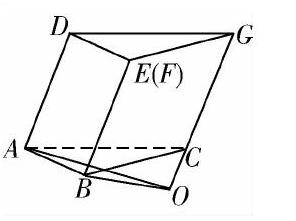
图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2所示.
(1)证明图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的四边形ACGD的面积.
二、解法赏析
(1)① 由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而四点A,C,G,D共面.
② 方法一:由已知得AB⊥BE,AB⊥BC,
故AB⊥平面BCGE.
又因为AB平面ABC,
所以平面ABC⊥平面BCGE.
方法二:取BC的中点H,连接AE,AH,EH.
由已知得,四边形BCGE是菱形,且∠EBC=60°,
三、教学建议
(一)回归教材,夯实基础
高考试题“源于教材”,既要体现考试的公平、公正,又“高于教材”,对中学数学教学做出有效检验,因此,要回归教材、挖掘教材、吃透教材.点、线、面判定与证明,是立体几何的基础,要认真学习几大公理及几条推论,对教材上的性质定理、判定定理的推导和证明熟记于心,很多高考题,源于教材例题与练习题的改编,平时复习要吃透教材,夯实基础.
(二)培养学生推理论证及直观想象能力
在讲授立体几何的过程中,让学生自己动手制作一些简单的几何模型可以帮助想象.观察几何模型中的点、线、面之间的位置关系,螺旋上升式地培养学生对立体图形的直观想象能力和辨别能力.开始学习必修2时要重点培养学生的作图能力.可以从最基础、最简单、最熟悉的正方体、长方体、三棱柱、三棱锥、球、圆柱、圆锥等开始画,逐步过渡到组合图形的画法.但是在作图过程中要树立起立体观念,通过作图训练使学生通过三视图,经过观察、推理、论证,能快速、准确无误地还原出立体图形.立体几何的直观想象并不是想当然的想,而是以题设的条件为依据,题目的求解为目的.此题就是利用图1平面图形经过翻折以后形成图2的立体图形,在翻折的过程中培养的学生的推理论证及直观想象能力.
(三)规范书写,加强运算
1.还要注重规范书写.很多学生的高考大题的作答十分不规范,字迹潦草,很多考生对作辅助线、证明、求解三个环节交代不清,表达不够规范、严谨,前因后果不连续,该用属于用包含,该用包含用属于,元素关系理解不清,符号语言不会运用等.这就要求学生在平时训练时养成良好的答题习惯,达到前有因后又果,书写时字迹工整,以教材上例题的答题要求、方法、步骤、推理过程作为蓝本.由于数学学科的特殊性,所以答题的规范性在每一次考试中都很重要,在立体几何大题中尤为重要,因为它更注重逻辑推理、直观想象.在按步骤给分的前提下,平时的每一道题的训练都要培养这种规范性答题,有利于提高得分.
2.加强运算.很多文科学生的计算能力不够强,本来过程全对,就是因为最后的计算出错而被扣分,此题很多学生都会运用余弦定理求解,公式运用正确,最后的结果错误,导致计算平行四边形的面积错误,有的学生前面都对,最后计算平行四边形的面积算错,实属不该.所以,在平时的每次训练中应加强学生数学运算的培养,提升计算准确度和计算速度.
(四)重视解题方法的总结与指导
高考立体几何所占的分值比较大,所以在平时的训练中应重视解题思路与方法的总结与指导.熟记重要的推理、证明以及重要结论有利于快速解决填空题或选择题,文科数学考试说明对建立空间直角坐标系不做要求,所以首先推荐的是定义法、几何法求解.
(五)着重培养学生数学核心素养
在必修2的教学过程中,由平面图到立体图是一个抽象的数学过程,立体几何的初步,空间几何体的表面积、体积,点、线、面之間的位置关系的推理、证明过程中体现出直观想象、逻辑推理、数学运算的数学核心素养.所以,教师在立体几何的教学过程中应加强核心素养的渗透.此题属于翻折类问题,通过不同的解法有利于提高学生分析问题、解决问题的能力,潜移默化地培养了学生的核心素养.
【参考文献】
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.

