2019年无锡中考数学压轴填空题的再思考

卞焕清

【摘要】中考数学压轴题具有覆盖知识面广、数量关系复杂、考查知识点较多、解题方法灵活多变等显著特点，同时压轴题更注重考查学生的分析能力、综合能力等数学基本素养，是学生能力的分水岭，也是区分学生学习能力的重要工具.本文基于2019年无锡中考数学压轴填空题，分析了问题中体现的数学思想、解题策略及解题技巧，同时也对教师在中考复习过程的教学提出了几点思路，以供参考.

【关键词】初中数学;中考压轴题;解题反思;中考复习策略

一、试题呈现

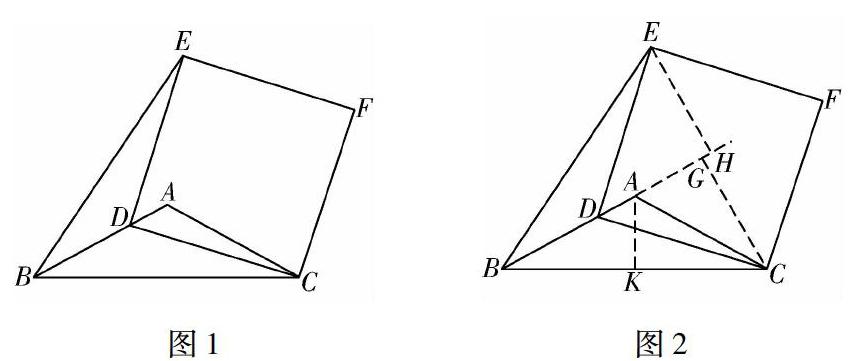
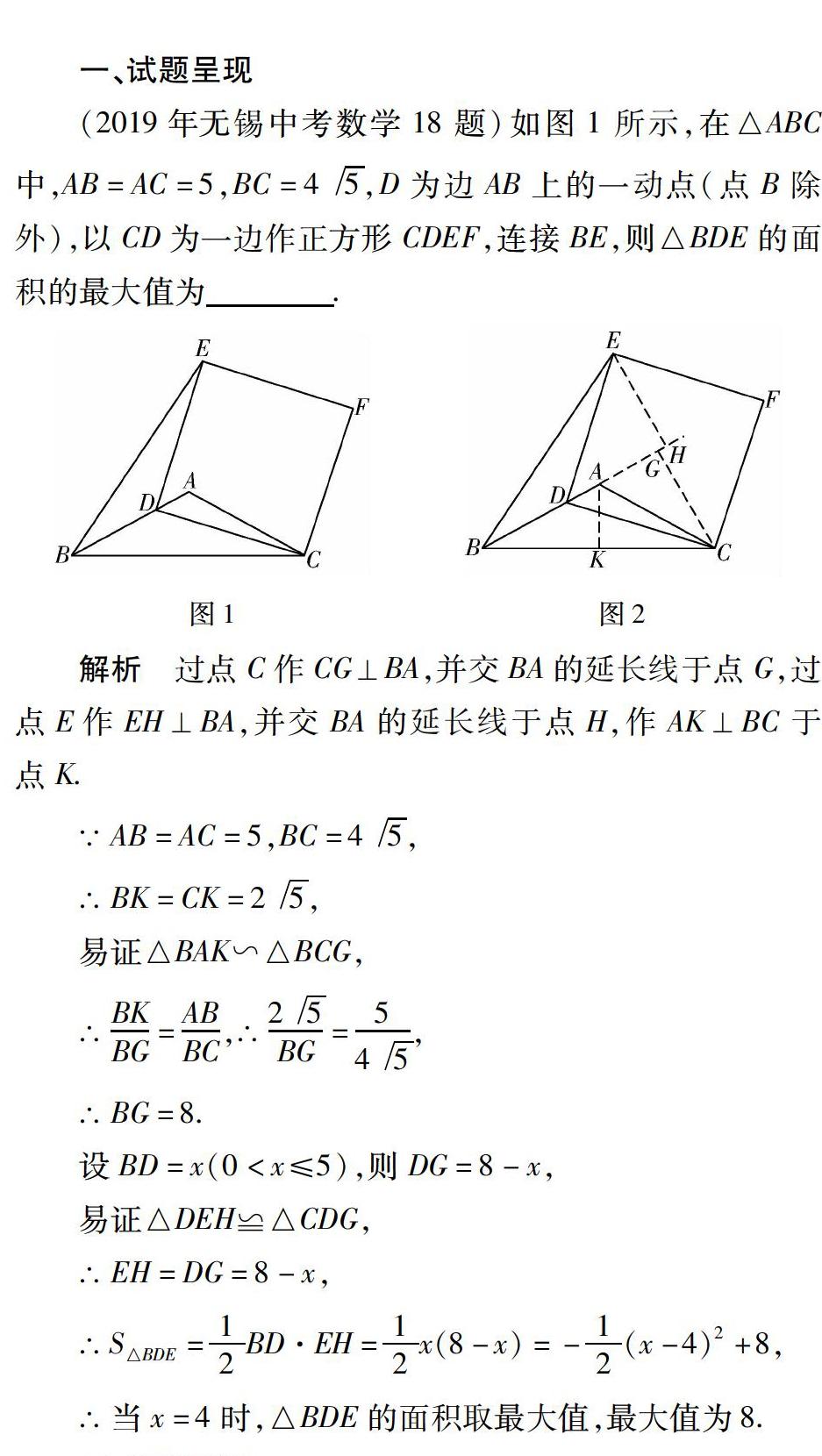
（2019年无锡中考数学18题）如图1所示，在△ABC中，AB=AC=5，BC=45，D为边AB上的一动点（点B除外），以CD为一边作正方形CDEF，连接BE，则△BDE的面积的最大值为.

二、解题反思

往年无锡中考压轴填空题多以线段和的最值问题为主，2019年无锡中考压轴填空题进行了大胆革新，考查了三角形面积的最值问题，不少考生感觉无从下手，或者解题方法烦琐、计算量大，不能很好地解决问题.

最值问题综合性较高，这类问题经常与特殊三角形（如等腰三角形、等边三角形）、特殊四边形（如正方形、菱形）、圆、平面直角坐标系、函数等知识点结合在一起，综合考查学生的逻辑思维能力、空间想象能力、分析问题及解决问题的综合能力[1，2].本题综合考查了三角形的相似、三角形的全等、三角形的面积计算、二次函数的最值问题，综合程度高，难度较大，不少考生无从下手，得分率较低.

最值问题一般也能分为函数模型和几何模型两种基本模型，其解题方法一般为：（1）代数方法，通过设未知数，依据题干中的相等或者不等关系建立方程（组）、不等式（组）来解决问题;（2）几何方法，将问题转化为常见的基本几何模型来解决（如“将军饮马”模型、“阿氏圆”问题、“胡不归”问题、垂线段最短等）[3，4].本题需要学生巧设未知数，利用含未知数x的函数表达式表示出三角形面积，从而求得面积的最值，这也体现了化归思想的重要性.因此，本题综合程度较高，难度较大，同时体现了不少数学思想，区分度较高，体现了中考数学压轴题应有的素质.

三、教学反思

中考数学压轴题的特点是知识覆盖面大、解法灵活多变、综合性强，面对中考数学的压轴题，尤其是包含动点的最值问题，笔者总结了在中考复习阶段教学中应注意的几个方面.

（一）注重典型问题的训练

中考第一阶段的复习注重的是对基础的复习及巩固，第二阶段的任务是对典型问题的全面认知，积累相关解题经验.因此，典型问题的专题训练是必不可少的，一般可以以近几年中考出现的热点问题为划分依据，进行专题内容的复习，同时也可以据此进行新题型的有针对性的训练.借此让学生熟悉不同的知识点之间的联系，探寻解题的策略.

例如，本题考查的是动态几何问题，其以正方形、等腰三角形为载体，AB上的动点为主线，研究三角形面积的最值为目标，集合了多种解题思想于一题.它考查了学生的空间想象能力和分析问题、解决问题等综合能力.当然，含有特殊图形的问题就一定要把握住特殊图形特殊背景，如本题中的等腰三角形及正方形的特殊性.在变化中发现不变的性质是分析解决动点问题的关键也是基本思路，同时还是动态几何问题中的核心本质.

（二）加强数学基本定理及模型的巩固

初中数学介绍了不少基本定理，在动态问题中最常用的就是“两点之间线段最短”“三角形三边关系”“垂线段最短”等.基于这些基本事实衍生出不少基本模型，在遇到新问题时，首先要确认的是该问题类似于以前熟知的哪一类基本事实或者模型，据此确定相应的解题方法，这也是解决类似问题的基本思路.因此，在中考复习中基本模型的训练是有必要进行强化训练的，同时加强不同模型之间的组合，提高对基本模型的辨识能力，提升解决动点问题的解题能力.

（三）注重举一反三

數学问题，特别是难度较大的压轴题是灵活多变的，性质、定理、公式在不同的条件背景下均会产生不同的题型，但是无论问题的形式如何改变，考查的本质是不会改变的.因此，需要对概念、性质、定理及问题从不同切入点，不同背景做出适当变化，从而达到融会贯通、举一反三的学习目的.教师应当更加注重引导学生通过一题多解、一题多变、多题化一的相关训练，增强学生思维的灵活性、变通性，巩固和深化学生对所学知识的理解，切实提高课堂教学效果.

（四）注重数形结合思想的渗透和培养

基础数学中的几何问题中蕴含着一定的数量关系，反之数量关系同时也常常可以通过结合图形做出直观的描述和解决.正如本题一样，几何问题通过代数方法求解是快速而且有效的.因此，数与形之间的相互转化往往是解决问题的利器.当然，在平时的练习过程中，教师也要着手培养学生的解题自信，提醒学生应以平常心对待每一次考试，沉着冷静地思考才有利于问题的解决.

总之，对于压轴题的教学，数学的基础知识和基本技能是“根基”，解题策略和方法是建立在双基之上的“上层建筑”.整个复习过程不能一味地强调攻坚克难，更要着眼于基础，做好基本题型的复习工作，着重数学方法的渗透和基本解题策略的指导，着眼于学生数学修养的提升，切实提高中考数学的复习效率.

【参考文献】

[1]钟珍玖.解题教学中存在的问题及应对策略——一道中考试题的考后思考[J].中学数学，2018（24）：83-84.

[2]刘春艳.理解试题内涵 把好教学方向——从一道北京中考试题说起[J].数学教育学报，2018（3）：35-38.

[3]蔡德清.中考数学压轴题的命题研究与反思[J].福建中学数学，2010（11）：11-14.

[4]王冰冰，苏圣奎，陈清华.2013—2015年福建省数学中考压轴题分类评析[J].福建中学数学，2018（1）：6-9.