在极限概念教学中如何培养学生的审辨思维能力

王俊行

【摘要】审辨式思维是一种判断命题是否为真或是否部分为真的思维方式.通过高等数学极限的概念的教学培养学生的审辨式思维能力有助于學生学习兴趣和创新能力的提高，从而提高教学质量.

【关键词】审辨式思维;高等数学;极限

在大学理工科中开设高等数学的意义不仅仅在于给学生后续专业课提供一个数学工具，更重要的是培养学生的数学思想、数学思维，特别是审辨式思维能力.尤其是在概念的教学中融入审辨式理论有意识地培养学生的审辨式思维能力有助于提高学生的创新能力.本文就极限概念的教学中培养学生的审辨式思维能力谈谈自己的做法.

一、理工科学生培养学生审辨式思维能力的意义

审辨式思维是一种判断命题是否为真或是否部分为真的方式.创新型人才最重要的心理特征是审辨式思维（critical thinking）.审辨式思维的核心内容是不懈质疑，包容已见，力行担责.审辨式思维是一种认知技能，也是最基本的探索工具.具有审辨式思维能力的人不会盲从，他们会用自己的头脑独立思索，他们会经过思考做出自己的判断.

对世界各国教育的研究发现与发达国家相比，中国学校中最缺乏的就是审辨式思维的培养.中国高考流行的一句话就是十年苦读三年模拟，中国学生的模仿能力是不容置疑的，但是创新能力不够，关键就是没有质疑的习惯，把科学当成了真理奉为教条.因此，学生到了大学以后更需要培养学生在这方面的能力，这比获取知识更加重要.因为网络时代的到来，人们获取知识的来源和渠道更加便利，我们不需要到图书馆查阅，一个数据库的查阅基本上都能满足我们的需要.学习也更加便利，网上视频教学可以循环看，基本上想学习什么都能找到.因此，给学生传授知识只是一个方面，教会学生思考的方法才是根本.要教会学生善于提出问题，不懈质疑，要教会他们自身反思和与此相关联的对异见的包容.这是与世界潮流相一致的，在科学界当今不再谈论“真理”，替代的是“科学理论”或“科学假说”.他们不再论断为“客观的世界图像”，而是说“可能的世界图像”.他们不再谈论“精确测量”，而是在接受“测不准原理”的前提下谈论各种可供选择的解释世界的方式.只有不断地质疑科学才能前行，我们的学生只有具备这样的能力才能有更大的作为.

二、在极限概念教学中培养学生审辨式思维的做法

数学是科学发展的基础.高等数学是理工科学生的必修课，是学好专业课的必备工具，也是开启学生创新思维的良好开端.由于高等数学是大一新生开始学习，是中学到大学的快速过渡的时期.中学数学研究的多数是常量，到大学后要从常量的学习到变量，第一个学习的概念就是极限.关于极限在中学阶段提到过，给出了极限的描述性定义，对“ε，δ”语言描述的极限概念讲的不多，学生也理解不深.我们做过调查，虽然学生学过极限的概念，但对极限的内涵理解模糊.而极限概念是贯穿微积分的桥梁和纽带，利用极限概念的教学培养学生的审辨式思维能力是绝佳的契机.一般教材中都是从刘徽的割圆术总结出数列的极限的概念进而讲函数极限.对数列极限是这样定义的：设{xn}为一数列，如果存在常数a，对任意给定的正数δ（不论多么小），总存在正整数N，使得当n>N时，|xn-a|<ε都成立，那么就称常数a是数列{xn}的极限，或者称数列{xn}收敛于a，记做 limn→∞xn=a或者xn→a（n→∞）.在这里可以提问学生N是不是唯一的？可以让学生讨论各抒己见，N满足条件，那么N+1是否也满足，依此类推.要找到的N成了无数个，这样得到的答案是否正确呢？慢慢培养学生不断质疑的能力.进一步引导学生思考由此得到了数列极限是一个静态的量还是动态的量呢？可以让学生思考13=0.333 3…和 limn→∞xn=a这里a和0.333 3…，哪个是静态的量，哪个是动态的量？让学生展开讨论.在学生讨论的过程中对不同的答案都要给予鼓励.这里可以给学生讲一下第二次数学危机，也就是关于微积分的危机.让学生知道微积分这个锐利无比的数学工具正是在不断的质疑争论中才得到了逐步完善.不断质疑、不断审辨是数学发展的根本.在讲完函数极限后给学生留下课后研讨题：你是如何理解极限的？10个人一个小组共同协作完成一篇小论文.给他们充足的时间进行交流和探讨，一个月后完成，通过组建的QQ群了解他们开展的情况.高数教学中不断强化学生的质疑能力有助于开发学生创新思维能力，激发他们的学习积极性，提高学习效率.

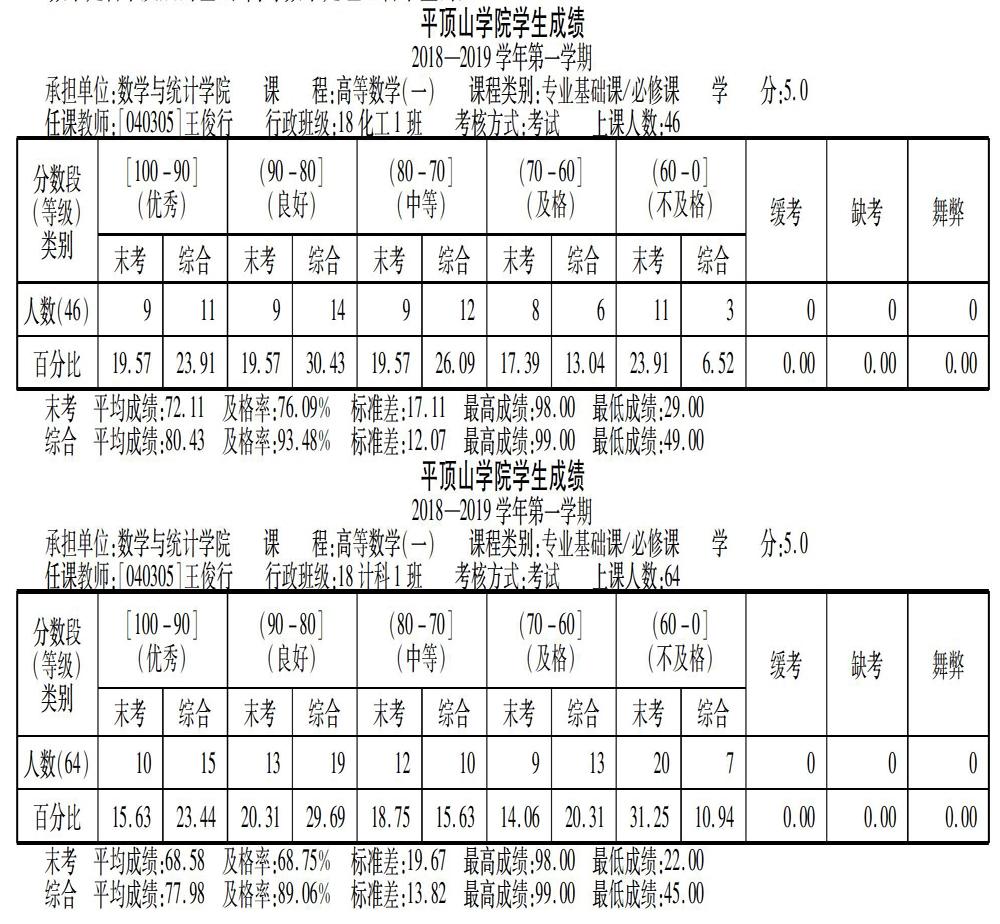
笔者在担任本校化学工艺和计算机科学两个专业高等数学教学的过程中做了大胆的尝试，化学工艺班有意识地强化提高审辨式思维能力，让学生广泛参与讨论共同探讨，计算机科学专业按照正常的教学进行.一年下来，在教改班每个知识点都有意识地激发学生审辨式思维能力，第一学期的期末考试成绩区别不大.

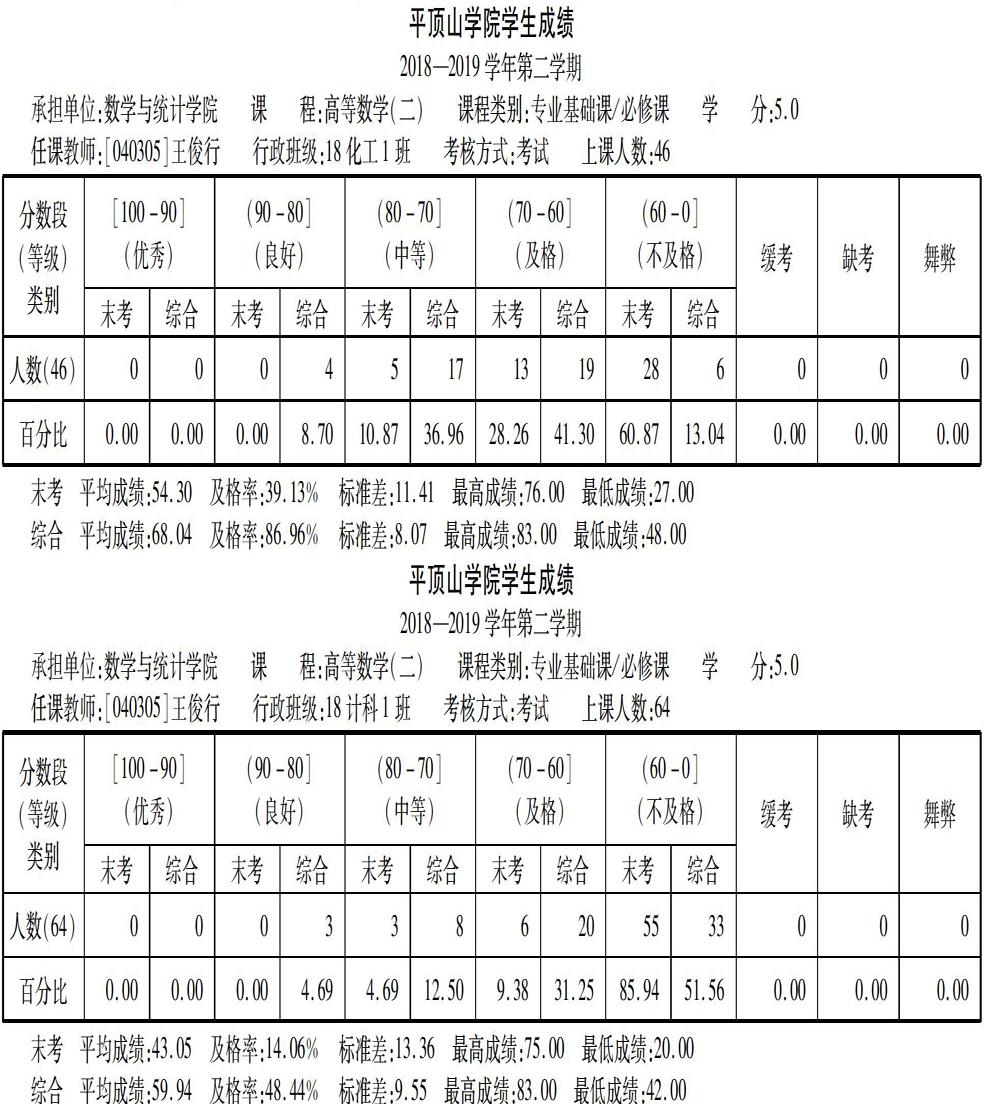
从以上可以看到第一学期下来成绩相差不大，第二学期差距就出来了，下边是第二学期的成绩.

第二学期成绩差异非常大，实施教改的化工班成绩明显好于计科班.出现这个现象，笔者进行了认真的调查和反思.

通过对两个专业学生的调查，了解到教改班的学生通过不断的质疑探索一直保持了非常高的学习兴趣，他们通过不断的质疑广泛的讨论，完成课后留下的小论文更加深入地了解了知识的根源，学习高等数学的兴趣保持得很好，他们认识到数学只是一门科学而不是真理，也需要不停地质疑，更需要不断地发展.计科班的同学从开始的热情高涨到后来逐渐逐渐倦怠，对高数产生的畏难情绪逐渐加重，探求知识的欲望下降导致成绩差异较大.教改中教师要付出额外的劳动还是比较多的，比如，引导学生查阅文献，辅导学生完成小论文等等，但是收效还是明显的，为提高公修课高等数学教学水平的探索提供一条新道路.