板柱节点冲剪破坏后的精细有限元分析
杨友喆,李 易,周大兴,陆新征,孙海林
(1. 北京工业大学工程抗震与结构诊治北京市重点实验室,北京 100124;2. 中铁建设集团有限公司,北京 100040; 3. 清华大学土木工程安全与耐久教育部重点实验室,北京 100084;4. 中国建筑设计研究院有限公司,北京 100044)
节点脆性冲剪破坏会引起板柱结构系统的内力重分布,极易引发整体结构的连续倒塌。国内外出现多起板柱结构的严重连续倒塌事故,例如韩国Sampoong 百货大楼和近年来国内在建地下车库倒塌事件,造成了严重的人员伤亡和财产损失。目前国内外抗连续倒塌设计规范主要针对以延性变形为主的钢和混凝土框架,尚未对板柱结构的抗连续倒塌设计进行详细规定[1―2],其原因在于相关研究还相对较少,不能为设计提供足够的参考依据。考虑到连续倒塌的科学研究和工程设计需要分析结构系统在大变形下的内力重分布,而板柱节点在冲剪破坏后仍能够继续以悬挂机制提供较大的承载力,因此认识板柱节点从冲剪破坏至悬挂机制的全过程受力机理和承载力变化规律是研究整体结构抗连续倒塌的基础。
在过去几十年,已经针对影响板柱节点冲剪强度和受力特征的关键结构参数开展了大量的试验和理论研究,包括混凝土强度、配筋率、板柱几何尺寸和边界约束条件等[3]。在试验数据的基础上,研究人员也提出了考虑钢筋贡献、混凝土几何尺寸效应的节点冲剪强度计算方法[4]。板柱节点虽然在小变形下发生冲剪破坏,混凝土开裂退出工作,但是穿过裂缝的楼板钢筋(特别是通长整体性钢筋)在大变形下仍能受拉承担较大荷载,进而对结构系统的连续倒塌行为产生重要影响[5]。近十几年随着对结构系统连续倒塌问题的关注,针对动力和静力加载条件下板柱、梁柱节点和子结构的冲剪破坏后受力性能[6-12]、结构可靠性[13]、结构碰撞倒塌[14]和相关理论计算[15-17]的分析也逐渐开展。
连续倒塌是结构系统力学行为,科学研究需要借助数值手段才能对结构系统的倒塌机理和内力重分布规律进行大量参数化的分析。在冲剪破坏前受力模拟方面:Navarro 等[18]采用有限元软件ABAQUS 建立三维精细模型研究了配筋率、板柱几何尺寸等参数对板柱节点冲剪承载力的影响;Liu等[19]建立了节点的宏模型,通过连接单元来实现板柱之间内力的传递。在冲剪破坏后受力模拟方面:Mirzaei 等[20]建立了一种冲剪破坏面的简化模型,采用连接单元控制剪切破坏和冲剪界面的非连续变形,冲剪破坏后受力由插入楼板的钢筋单元模拟。由于目前尚缺少节点冲剪后的力学模型和承载力计算方法,简化模拟方法虽然计算高效但连接单元的参数还需要试验确定,而建立理论模型和计算方法需要借助可以反映冲剪破坏界面形态、冲剪后钢筋混凝土相互约束的精细模型。随着计算力学的发展,目前的通用有限元软件已经能够较好的模拟上述复杂受力行为。基于精细有限元模型可以对节点开展细致的受力机理和承载力变化规律研究,满足结构工程研究的需要,但目前这部分研究非常有限。
为开展板柱节点冲剪破坏后受力分析,本文采用通用有限元软件LS-DYNA 建立了板柱节点的精细有限元模型。通过3 类典型板柱节点冲剪试验的模拟对数值模型有效性进行了验证。针对面内约束的节点试验进行了扩展分析,以展示该模拟方法对节点冲剪后受力研究的应用,包括冲剪后承载力贡献的量化分析、板厚和配筋率对冲剪全过程受力行为的影响、现有冲剪和悬挂机制承载力计算方法的检验。
1 有限元模型
1.1 结构模型
混凝土采用8 结点三维实体Lagrangian 单元,为了节省计算时间并且避免单元的非物理变形,使用了缩减积分规则和1 型粘性沙漏控制方法。钢筋采用2 结点一维Hughes-Liu 单元,其截面采用默认的2×2 高斯积分,可以考虑单元受轴向力、双向弯曲和横向剪切的行为,有效模拟冲剪破坏后裂缝间的大变形钢筋。通过网格敏感性分析,在冲剪区域和其他区域的混凝土和钢筋单元分别采用精细和粗糙的网格尺寸,以保证计算精度的同时提高计算效率。
1.2 材料模型
混凝土参考相关文献的建模方法采用CSCM模型(*MAT_159/*MAT_CSCM)[21―24],该模型可以模拟混凝土材料的约束效应和峰值后软化等特征,因此在钢筋混凝土子结构连续倒塌的模拟中得到广泛应用[18-20]。特别是该模型在有限侧压下能够较好地考虑受拉和受剪行为,非常适合混凝土板柱节点的冲剪破坏模拟。混凝土弹性体积模量K和剪切模量G采用CEB-FIP[25]推荐的泊松比γ和弹性模量E计算,塑性阶段的材料参数由无侧限抗压强度、骨料尺寸和单元尺寸计算求得。图1 给出了圆柱体抗压强度为27 MPa 的无约束单轴混凝土拉压骨架曲线。考虑钢筋是单轴受力,钢筋材料采用分段线性弹塑性材料模型(*MAT_024/*MAT _PIECEWISE _ LINEAR_PLASTICITY)。通过弹性模量定义弹性阶段,通过单轴拉伸试验得到的工程应力-应变曲线来定义塑性阶段。考虑已有节点试验均为静力加载,因此模型中不考虑材料应变率的影响。
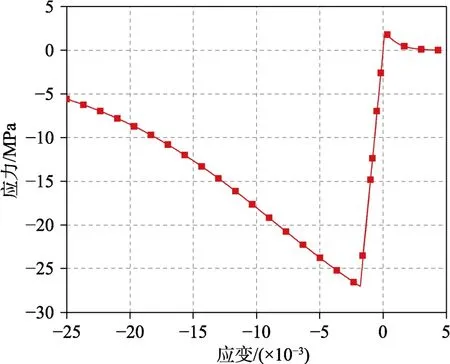
图1 CSCM 模型的单轴应力-应变曲线 Fig.1 Uniaxial stress-strain relationship of CSCM model
1.3 约束与破坏
在冲剪界面以外,试验中钢筋和混凝土能够完全共同工作,因此在数值模拟中不考虑钢筋混凝土间的粘结滑移,通过关键字*CONSTRAINED_ BEAM_IN_SOLID 定义钢筋和混凝土完全约束,共同作用。即钢筋梁单元结点与混凝土实体单元结点的速度和加速度保持一致。而在冲剪界面及其附近出现剪切破坏的混凝土大面积脱落,数值模拟中采用生死单元方法,结合破坏准则将达到极限剪切应变的混凝土单元删除,此时主要依靠钢筋的大变形受力抵抗外荷载,不同钢筋层之间的相互接触决定了力的传递路径。分析中通过关键字*CONTACT_ AUTOMATIC_GENERAL 定义钢筋之间的接触关系,摩擦系数设为0,该接触关系为单面接触,即在处理梁单元相互接触过程中不需要定义接触面与目标面,程序能够搜索模型中的所有外表面并沿着单元长度方向检查是否存在穿透现象。对发生接触的钢筋在接触面的法线方向考虑接触受力,该关键字保证钢筋在大变形下只发生接触不发生穿透,实现悬挂机制下钢筋相互作用模拟。为了模拟混凝土剪切开裂和钢筋断裂,通过关键字*MAT_ ADD_EROSION 激活生死单元功能,分别采用极限剪切应变和最大有效拉应变作为混凝土和钢筋的破坏准则。冲剪破坏和冲剪破坏后的受力行为与混凝土剪切破坏和钢筋断裂失效相关。由于材料的离散性,目前很难给出统一的失效准则来准确模拟所有试验,因此在本文模拟时采用试错法将经验值与试验中混凝土实际破坏情况进行对比,调整后试算获得。Pham 等[24]在确定混凝土破坏应变时也采用该方法。在确定钢筋断裂应变时,通过将数值模拟与试验承载力曲线中因为钢筋断裂而出现掉点的位移时刻和相应承载力大小进行对比试算,从而确定其断裂应变。每个试验的材料失效准则(混凝土极限剪切应变εeps和钢筋最大有效拉应变εeff)均在相应部分给出。节点冲剪试验通常约束楼板然后对柱头进行位移加载,为了防止模拟时柱头加载点处的应力集中,在柱头上设置一个仅允许竖向平移的刚体,通过刚体位移控制加载,采用关键词*DATABASE_CROSS_SECTION_SET 和*DATA- BASE_SECFORC 读取柱头刚体的等效反力,得到节点的承载力。
2 试验验证
在实际结构中,周围楼板对板柱节点产生面内约束作用,该约束作用使得冲剪后穿过裂缝的钢筋仍能传力,对结构冲剪破坏后承载力产生重要影响。不考虑这种约束作用会忽略小变形下混凝土压膜和大变形下钢筋的拉膜效应,不能反映结构实际冲剪破坏前后的受力机理和承载力。以往的大量试验研究集中在冲剪破坏方面,试件均采用无约束节点,试验仅进行到冲剪破坏为止。随着连续倒塌研究的开展,对约束节点大变形受力行为的认识变得更加迫切,但目前仅有有限的约束节点的冲剪后受力试验被报道[26-27]。为了验证本文模拟方法的准确性和适用性,分别对无面内约束的冲剪试验、无面内约束的冲剪后试验以及有面内约束的冲剪后试验进行模拟。
2.1 无面内约束冲剪试验
文献[28]节点冲剪试验中四边简支试件B-4 的试件材料信息如表1 所示。该节点模型的几何模型、材料模型、约束和接触关系均采用前文方法定义。由于该试验仅加载到冲剪破坏发生前,节点未发生明显破坏,因此不考虑钢筋和混凝土的单元删除。考虑对称性,只建立了1/4 模型以节省计算时间,镜像边界处采用对称约束,如图2(a)所示。对试件的每个简支边界采用以下方式模拟:仅约束板底边缘一列结点在竖直方向的平动位移,释放其他5 个自由度(包括2 个平动和3 个转动自由度)。试验与模拟的承载力-位移曲线对比如图2(b)所示,模拟与试验结果能够较好的吻合,冲剪承载力误差在1%以内。

表1 试件材料信息(无面内约束节点冲剪试验) Table 1 Material details of the specimen (Punching shear test of the joint without in-plane constraints)

图2 模拟结果(无面内约束节点冲剪试验) Fig.2 Numerical results (Punching shear test of the joint without in-plane constraints)
2.2 无面内约束冲剪后试验
文献[16]对四边简支节点进行了冲剪破坏后的加载试验,其中试件PM10 材料信息如表2 所示。该节点模型的几何、材料模型,约束、接触关系以及破坏准则的定义均采用上述通用方法,并且考虑单元的删除功能以模拟脆性冲剪破坏过程,边界条件的定义采用与2.1 节相同的方法。试验与模拟的承载力-位移曲线对比如图3 所示,冲剪及冲剪后第一峰值点承载力的误差分别为2.6%和11.2%,其中冲剪前的模拟非常准确,冲剪后的模拟有一定的 偏差。

表2 试件材料信息(无面内约束节点冲剪后试验) Table 2 Material details of the specimen (Post-punching test of the joint without in-plane constraints)

图3 模拟结果(无面内约束节点冲剪后试验,εeps=0.016) Fig.3 Numerical result (Post-punching test of the joint without in-plane constraints, εeps=0.016)
2.3 面内约束冲剪后试验
文献[27]开展的板柱节点试验中,楼板和边界梁整体现浇,边界梁可为楼板提供面内约束。本文选取其中向上冲剪系列的3 个变参数试件进行分析,试件的材料信息如表3 所示。标准件UPS-1 板厚为90 mm,和UPS-1 相比,UPS-2 将板厚减小20 mm;UPS-3 将配筋率增大30%,标准件UPS-1的数值模型如图4 所示。

表3 试件材料信息(面内约束节点冲剪后试验) Table 3 Material details of the specimens (Post-punching test of the joints with in-plane constraints)

图4 UPS-1 几何模型 Fig.4 Geometric model of UPS-1
试验与模拟的承载力-位移曲线对比如图5 所示。可以看到,与无面内约束试件在大变形阶段承载力基本保持水平相比(如图3 所示),约束节点在冲剪破坏发生后,依然可以通过钢筋受拉提供承载力贡献,因此节点的刚度和承载力在悬挂机制阶段能够稳定提升,最终提供较大承载力。在冲剪破坏后结构虽然受到较强损伤,但是残余承载力的幅值仍然不可忽略,这对结构系统的内力重分布和连续倒塌的破坏传播规律具有重要影响。考虑到造成初始局部破坏的灾害是小概率事件,目前连续倒塌设计采用允许局部破坏发生但是严格限制破坏传播的策略,安全、经济地实现抗连续倒塌目标。对板柱结构,这意味着节点已经发生冲剪破坏,进入悬挂受力阶段。由于钢筋断裂后材料破坏具有随机性,承载力发生较大波动,因此抗连续倒塌设计应主要关注冲剪至钢筋断裂间(冲剪后第一子阶段内)节点的力学行为,该阶段结构受力性能对抗连续倒塌设计有着重要意义。表4 和表5 分别给出了冲剪和冲剪后首个峰值点对应的位移和承载力对比,从关键点的数值看,模拟结果与试验吻合较好,平均误差均在12.3%以内。从承载力曲线看,冲剪破坏前的刚度、承载力发展吻合较好,冲剪后的承载力曲线和试验具有一定的偏差。

图5 模拟结果(面内约束节点冲剪后试验)Fig.5 Numerical results (Post-punching tests of the joints with in-plane constraints)
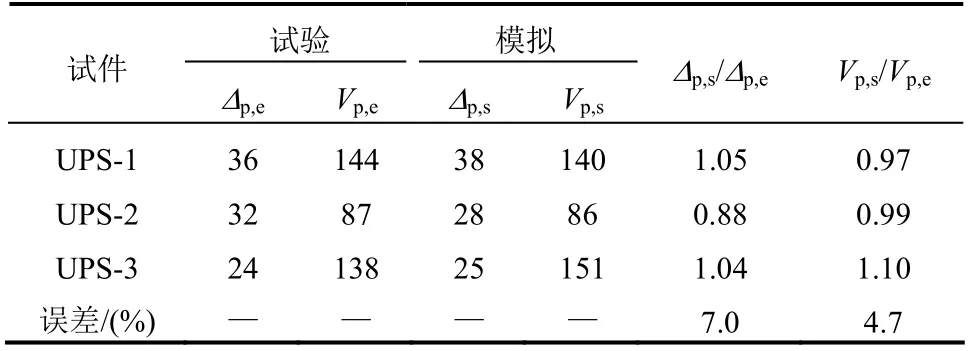
表4 冲剪变形与承载力对比 /mm, kN Table 4 Comparisons of punching shear deformation and capacity
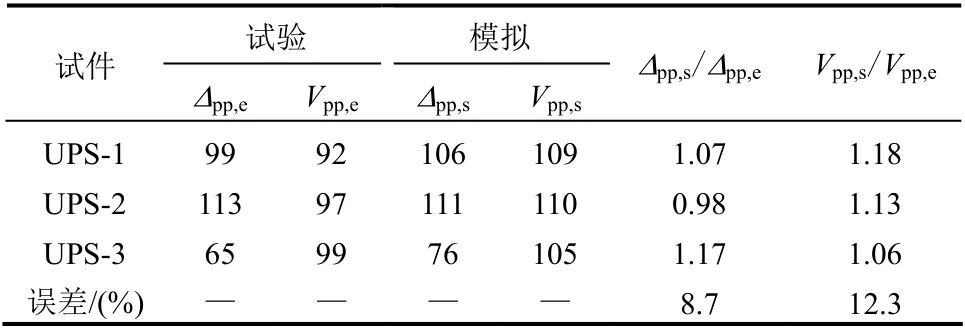
表5 冲剪后变形与承载力对比 /mm, kN Table 5 Comparisons of post-punching shear deformation and capacity
以标准件UPS-1 为例说明节点的典型破坏现象,如图6 所示。冲剪破坏时板底呈放射状裂缝,冲剪破坏后混凝土发生剪切破坏并出现大面积脱落,钢筋部分从混凝土中拔出并发生大转动变形,钢筋间相互约束共同受力,数值模拟的受力模式与试验完全一致。
本文有限元模拟的误差主要在于:1) 冲剪时刻残余承载力,即冲剪机制转换点处(最低点承载力)的试验值大于模拟值(如图3、图5 所示);2) 大变形阶段下钢筋断裂后承载力下降明显(图5)。这是因为生死单元技术通过删除达到破坏准则的混凝土单元来模拟冲剪区域的剪切裂缝,而实际试验中冲剪破坏发生时虽然冲切锥体与楼板发生分离,但破坏的混凝土不会全部发生剥落,在破坏裂缝处的混凝土骨料咬合力和纵筋的销栓作用会缓解这一时刻的承载力骤减,部分混凝土嵌固在钢筋间,为节点在大变形下提供了残余承载力。冲剪破坏后,破坏界面上的钢筋与混凝土的变形和相互工作更趋向于“机构”而非“结构”,其相互作用难以用基于连续介质力学的有限元进行精确模拟,因此在对应的破坏变形上出现误差。不过总体来看,本文的建模方法可以准确模拟板柱节点从小变形受弯到脆性冲剪破坏,直至冲剪破坏后钢筋断裂时的受力状态,能够满足科学研究和工程实践的需要。
3 板柱节点冲剪后受力分析
面内约束节点试件的边界条件最接近实际情况,因此以2.3 节的试验和已建立的模型为基础进行扩展分析,展示精细有限元模型在抗倒塌受力分析方面的优势。


图6 UPS-1 试件不同阶段破坏模拟对比 Fig.6 Comparison of damage modes of UPS-1 at different stages
3.1 不同钢筋层的冲剪后承载力贡献
分析各层钢筋的承载力贡献是建立冲剪后承载力计算模型的基础。为了方便理解,将试验楼板反画,得到与实际情况一致的节点冲剪破坏后示意图,如图7 所示,虽然一些非穿柱的楼板钢筋也发生了变形,但是最终这部分钢筋的力通过穿柱钢筋传到柱头上,因此穿柱钢筋的变形和受力是控制冲剪后节点承载力的关键。由于板内4 层钢筋的位置和相互约束关系的差异,不同层钢筋变形和应力水平也各不相同,会影响其对节点冲剪破坏后承载力的贡献。由于倒塌试验中极端复杂的受力条件,材料应变片很容易在大变形下发生破坏,因此难以稳定测量各层钢筋在冲剪破坏后的受力状态。本文从验证后的数值模型中提取每根穿柱钢筋的轴力并根据该单元的变形角度求得其竖向分力,以分析其抗倒塌承载力贡献。各部分钢筋的冲剪后承载力及其对总承载力贡献的百分比如表6 所示,整体钢筋和受弯钢筋对总承载力贡献的百分比分别为42%和58%。和受弯钢筋相比,穿柱的整体钢筋虽然数量少了50%,但由于发生了较大的转动变形,能够提供更大的竖向分力,最终其承载力贡献仅比受弯钢筋低16%。

图7 冲剪破坏后板柱节点受力状态 Fig.7 Post-punching mechanism of slab-column joint

表6 不同钢筋层对冲剪破坏后的承载力贡献 Table 6 Contribution of different steel layers to post-punching capacity
3.2 结构参数对节点受力性能的影响
面内约束对节点承载和变形能力均产生影响,但目前考虑约束的试验仍然非常有限。本节对上文面内约束节点的标准试件进行扩展分析,其中配筋率从已有的0.8%分别扩展到0.9%、1.0%和1.1%,板厚从已有的90 mm 扩展到70 mm、80 mm、100 mm,其余参数保持不变。配筋率和板厚对节点冲剪和冲剪后第一峰值点的承载力和变形的影响如图8 所示。需要注意的是,对变结构参数的试件扩展模拟时,所有试件的钢筋和混凝土破坏应变均与标准件保持一致。


图8 不同结构参数节点的模拟结果 Fig.8 Numerical results of the joints with different structural parameters
随着配筋率依次增加13%、25%和38%,冲剪前的割线刚度分别相差29%、50%和69%。同时,更高的配筋率下混凝土剪应变发展更快,导致冲剪位移随着配筋率的提高依次减小14%、22%和29%,节点延性降低使得最终节点冲剪承载力Fp仅依次增加9%、11%和20%,小于配筋率以及冲剪前割线刚度的增加幅度。冲剪破坏后节点承载力主要由钢筋提供,随配筋率增加冲剪破坏后第一阶段的节点刚度最大增加了58%,但是由于配筋率提高造成冲剪破坏提前发生,穿柱钢筋受力更加集中,在更小的位移下达到断裂应变,因此冲剪破坏后的承载力Fs1最大仅相差10%。综上所述,与冲剪以及冲剪破坏后节点的承载力相比,配筋率的提高对楼板刚度的影响更为显著。随着板厚的增大试件冲剪前后承载力分别提高了91%和33%,这是因为冲剪破坏前楼板以受弯抵抗外荷载,板厚提高了楼板的受弯承载力。板厚不影响混凝土剪切应变发展,所以试件冲剪破坏的位移变化较小。随板厚增加冲剪前的割线刚度依次为 2.8 kN/mm、3.5 kN/mm、4.3 kN/mm、6.1 kN/mm,而冲剪破坏后第一阶段的刚度依次为1.0 kN/mm、1.3 kN/mm、1.3 kN/mm、1.6 kN/mm,两组刚度分别最大相差118%和60%。板厚对冲剪后强度的影响较小,这是由于冲剪破坏后主要由钢筋受力,因此板厚改变对试件刚度影响不大,但是混凝土会影响局部钢筋约束条件,此时大变形下复杂的局部受力状态导致钢筋断裂发生在不同位移,造成刚度尚有一定程度的差异。
3.3 既有承载力计算方法验证
按照欧洲[29]、美国[30]、澳洲[31]和中国[32]的混凝土结构设计规范对上文分析的11 个试件进行节点冲剪承载力验算,结果如图9 所示。本文对比试验值与规范值主要基于以下目的:1) 规范计算方法具有理论背景,可以对比分析现有规范中冲剪承载力计算方法考虑因素(如结构参数,计算假设);2) 有规范承载力计算方法基于无约束节点试验,本文验证可以评估原有方法在设计实际有约束节点时的承载力储备。

图9 各国规范冲切承载力计算结果对比 Fig.9 Comparisons of punching capacities based on different codes
欧洲规范考虑了钢筋贡献,且计算假设的冲剪破坏面范围较大,其计算承载力稍高。美澳中三国规范考虑的冲剪破坏面范围大小相同,并且材料剪 切破坏强度也较为接近。如采用标准件UPS-1(板厚90 mm)的参数,将美澳中三国规范的冲剪强度整理成以混凝土圆柱体抗压强度fc为变量的表达式,依次得到0.33fc0.5、0.34fc0.5、0.27fc0.55,三者相差不大。 考虑冲剪是小变形破坏,楼板在面内约束下产生压膜效应对混凝土板的抗剪承载力有一定的提高,而现有规范方法主要基于无约束节点试验结果,计算表明欧美澳中四国规范在计算约束节点冲剪强度值时的承载力储备分别为36%、53%、62%和64%,普遍偏于保守。
现有2 个板柱节点冲剪破坏后的承载力计算方法,其中Habibi 等[15]认为所有锚固穿柱钢筋的应力性钢筋锚固可靠会达到极限强度,而支座负弯矩筋状态均取于混凝土抗崩裂强度;Ruiz 等[16]认为整体的约束不足,其应力状态由混凝土崩裂强度控制。下面根据这两种计算方法分别对本文10 个向上冲剪破坏后节点试验进行计算,结果如表7 所示。上述两种方法的计算结果普遍偏于保守,仅PM10 试件的理论计算值均大于试验值。这由于验算的试件中除了PM10,其余试件均考虑周边楼板对节点的面内约束作用,因此在试验/模拟中支座负弯矩筋能够充分受力在加载过程中均出现被拉断现象,而两种计算方法中均以约束钢筋的混凝土达到崩裂强度来定义支座负弯矩筋的失效,低估了其承载力贡献,导致最终计算结果偏于保守。

表7 冲剪破坏后承载力计算结果 /kN Table 7 The calculation results of post-punching capacities
4 结论与展望
本文建立了板柱节点冲剪破坏的精细有限元模型,对面内约束条件下节点冲剪破坏全过程的受力行为进行分析,得到以下结论:
(1) 精细有限元模型能够有效模拟冲剪时节点脆性破坏、混凝土剪切开裂,以及冲剪后钢筋断裂、大变形下钢筋间相互作用。三类节点试验冲剪前后承载力的模拟误差最大为12.3%。
(2) 面内约束节点的整体性钢筋和受弯钢筋对冲剪后承载力贡献的百分比分别为42%和58%;配筋率提高对节点刚度的提升更为显著,配筋率提高38%时节点冲剪前后的割线刚度分别提高69%和58%,而相应的承载力仅提高20%和10%;板厚增加对节点冲剪破坏前受力影响大,板厚增大43%时节点冲剪前后的割线刚度提高118%和60%,相应的承载力提高91%和33%。
(3) 约束节点的实际冲剪强度值均高于各国规范计算值,至少有36%的承载力储备,其中欧洲规范考虑了钢筋贡献且计算冲剪破坏面较大因而设计计算值稍高,美澳中三国规范的冲剪破坏面、材料抗剪强度接近,因此设计计算值相差较小。

