基于代理模型的差分进化约束优化

薛 锋，史旭华，史非凡

（宁波大学信息科学与工程学院，浙江宁波315211）

（∗通信作者电子邮箱520286179@qq.com）

0 引言

系统优化包括无约束优化和约束优化，在科研、管理、工业等方面都发挥着重要作用。现实世界中的许多问题本质上都是优化问题。最开始，研究者使用各种传统优化算法来解决优化问题，传统优化算法一般针对的是结构化的问题，其问题与条件的描述都较为明确，可以在特定条件下产生全局最优解。对于解决单极值问题，传统的优化算法已足够好，然而，对于解决多变量、高复杂度的多极值优化问题，使用传统优化方法效率不高，容易陷入局部最优。为了解决这一问题，有研究者提出了进化算法（Evolutionary Algorithm，EA），如遗传算法、差分进化、粒子群优化等。这些算法在解决复杂优化问题时表现出了更好的性能。

相较于无约束的优化问题，约束优化问题中多了各种约束条件。约束条件通常包含等式约束、不等式约束以及变量的上下界约束。在进化计算领域，越来越多的研究者使用进化算法来解决约束优化问题。对约束的处理，提出了多种约束优化进化算法（Constrained Evolutionary Optimization Algorithm，COEA）［1］，如变量约简策略［2］、简单多种群进化策略［3］、混合约束优化进化算法［4］等。

约束优化问题通常可描述为:

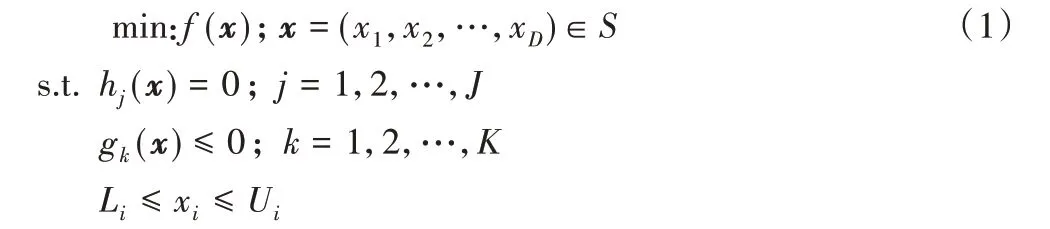
对约束的处理主要以下6 种方法［5］:罚函数法［6］、可行性规则［7］、多目标优化法［8］、随机排序法［9］、ε 约束处理法［10］、混合法［11］。

实际上，约束处理技术是为了确定一个标准，以此来比较亲本和后代的优劣。罚函数法的主要思想是根据种群中个体的约束违反度来构造惩罚项，然后将惩罚项与目标函数相结合来构造出一个惩罚适应度函数，从而将带有约束的优化问题转换成无约束的优化问题来处理；但罚函数法存在着参数设置困难、实际使用效果不佳的问题［6］。多目标优化法是将约束优化问题转换为多目标优化问题，然后运用多目标优化方法来解决转换后的问题，该方法具有较好的收敛结果和性能；但是其消耗的计算资源也是巨大的［8］。随机排序法采用一个概率参数来决定是根据个体的约束违反程度还是根据其目标函数来评判两个个体的优劣；但也存在着相关参数设置困难的问题［9］。ε 约束处理法是通过预先设定ε 值，然后基于个体的约束违反度将决策域分为不同的区域，在不同的区域，对可行解和不可行解采用不同的方法进行比较，其缺点是比较耗时［10］。

可行性法则是Deb 于2000 年提出的一种约束处理方法，该方法通过一定的准则对两个候选解进行比较，从而选择出其中较优的一个。相对于其他方法，可行性法则能够更快地找到可行解，且该方法容易实现，不需要设置额外参数，可以适用于各种场景。

一般来说，进化约束优化算法有两个主要目标:1）快速进入可行域；2）找到最优解。大多数进化约束优化算法为了尽快进入可行域而依赖约束条件对个体进行比较，从而忽略了目标函数的影响。这样不利于算法的快速收敛。对此，本文提出了基于代理模型的差分进化约束优化算法（Surrogatebased Differential Evolution Constrained Optimization Algorithm，SDECOA）。SDECOA 将目标函数的信息和约束条件作为个体选择的评价，运用到算法中，并且结合了代理模型来提高解决耗时计算问题的计算效率。

SDECOA 使用差分进化算法来进行搜索，并运用可行性规则来对个体进行比较。在进化过程中，如果差分进化产生的后代根据可行性规则进行比较比父代差，但是其目标函数值比父代更优，则将该子代存入备用种群存档中，然后通过一种替换机制来用存档中的个体替换种群中的某些个体。此外还提出了一种突变策略来防止种群陷入不可行区域。在计算出第一代个体的目标函数值后，使用这些数据来建立目标函数的代理模型，在之后对子代的评估都通过代理模型来进行，这样就可以大幅减少目标函数的调用次数，从而提高算法效率。

1 背景知识

1.1 代理模型

对目标函数构建代理模型已经成为一种用来优化现实世界中复杂问题的实用方法。因为使用代理模型能有效地降低计算成本，从而实现更低的预算。代理模型的思想是对耗时计算的目标函数建立一个近似的替代模型，用这个模型来替代进化计算过程中对目标函数的调用，从而减少耗时计算的次数。

在解决复杂优化问题上，可供选择的代理模型［11］有许多:克里金（Kriging，KRG）模型、高斯过程（Gaussian Process，GP）模型、多项式响应面（Polynomial Regression Surface，PRS）模型、径向基函数（Radial Basis Function，RBF）模型、后向传播神经网络（Back Propagation Neural Network，BPNN）模型、支持向量回归（Support Vector Regression，SVR）模型等。

以上这些代理模型的理论基础和适用范围均不相同，本文主要使用克里金模型、多项式响应面模型和后向传播神经网络模型来对目标函数进行拟合。

1.2 可行性规则

由Deb提出的可行性法则是当前应用最受欢迎和最有效的约束处理技术之一，在可行性法则中，当需要对两个解xi和xj进行比较时，在满足以下条件之一时，xi比xj更优:

1）xi是可行解而xj是不可行解；

2）xi和xj都是可行解，但xi的目标函数值更小；

3）xi和xj都是不可行解，但xi的约束违反度值更小。

2 基于代理模型的差分进化约束优化算法

2.1 算法整体框架

约束优化进化算法主要包括两个部分:约束处理技术和搜索算法。因为差分进化算法具有简单、高效、易于使用等优点，所以本文使用它作为搜索算法。

针对可行性规则处理约束速度快但是可靠性较差的特点，本文使用了一种利用目标函数提供的信息来提高其鲁棒性的方法。通过将目标函数的信息与可行性规则相结合，可以使得算法在约束条件和目标函数之间达到平衡。

如算法1 所示，首先初始化种群Pt，计算出当前种群中每个个体的目标函数值和约束违反度值，并使用这些数据建立目标函数的代理模型。其次对种群中的每个个体xi，t通过差分进化产生一个试验个体vi，t，使用代理模型计算试验个体的近似目标函数值，然后根据可行性规则对xi，t与vi，t进行比较，将更优的一个加入下一代种群。如果vi，t能加入下一代则用真实目标函数计算出其真实的目标函数值。如果vi，t不能进入下一代但是却有更小的目标函数值，则将其加入备用存档中。

2.2 差分进化算法的改进

差分进化算法［12］是一种启发式随机搜索算法，该算法的主要特点是利用种群中的个体间的差异向量来对个体进行变异操作，其交叉与选择操作与遗传算法大致相同。该算法原理简单、鲁棒性强、受控参数少，求解质量高且收敛速度优于其他一些进化算法。

本文使用一种改进的差分进化算法来对最优解进行搜索。针对原始的差分进化算法容易陷入局部最优的问题，本文对差分进化算法进行了改进，与原来的差分进化算法不同的是，改进后的差分进化算法中的个体不仅仅向种群中随机的其他个体获取信息，而且还有相同的可能向种群中的最优个体获取信息。

如算法2 所述，其中k1、k2、k3 是［1，NP］中互不相同的整数，F 是缩放比例因子。首先取一个［0，1］的随机数rand，若rand＜0.5，则只从种群中的其他随机个体获取信息；反之则额外从最优个体获取信息。

2.3 替换机制

替换机制的目的是通过将当前种群中的一些个体用备用存档中的个体来替换从而避免可行性规则过于贪心的问题。

如算法3 所示，为了避免只在可行域的局部区域实行替换机制，该算法先将种群中的个体按照目标函数值的大小降序排列，再将其分为相同尺寸的N 个部分。然后选择种群的第一部分中约束违反度最大的个体xa和备用存档中约束违反度最小的个体xb，如果xb的目标函数值小于xa的目标函数值，则用xb替换xa。再对接下来的每一个部分进行同样的处理。

2.4 变异策略

由于在求解约束优化问题时，种群很容易陷入不可行区域的局部最优，这样就会导致在迭代结束时无法找到最优解。出于这方面的考虑本文使用了一种种群变异策略，该策略仅在种群中的所有个体全部为不可行解时才会用到。

失业后的程晓只得开着凯迪拉克去机场和火车站的路口揽客。一天，他送一个齿轮厂的小老板去一家大公司谈业务，那位小老板要程晓在那家公司的大楼下等着把他送回去，来回仅40公里路程，对方竟开出了400元的高价。

如算法4 所示，如果当前种群中的所有个体都是不可行解，则从种群中随机选择一个个体进行变异操作，生成新的个体来替代当前个体，从而避免无法进入可行区域的情况发生。

3 仿真

3.1 与其他约束优化算法的比较

为了测试本文所提出的算法的有效性，选取CEC2006 中比较典型的测试函数来对算法进行测试。初始种群数设置为80，对于不同复杂度的目标函数设置不同的最大适应度评估次数。使用软件为Matlab r2018a，对于每一个测试函数都在相同的条件下运行20次。

将 本 文 算 法 与 FROFI（Feasibility Rule with the incorporation of Objective Function Information）算法［13］和内部罚函数进化策略（Interior Penalty based Evolution Strategy，IPES）算法［14］进行比较。对于每一种算法都设置相同的最大适应度评估次数，然后分别从三个方面比较:最优值、平均值和方差。从表1 中可以看出，本文提出的SDECOA 能够在较少的适应度评估次数下得到更优的结果，而且方差最小，说明SDECOA 的效果最稳定；而FROFI 算法和IPES 算法在同样的适应度评估次数下的结果不如SDECOA。对于g05、g10、g14、g15这四个函数，FROFI算法无法在较少的适应度评估次数下求出结果；对于g04、g05、g12，IPES 算法也无法在给定的适应度评估次数的限制下求得结果；但SDECOA 却能在同样的适应度评估次数限制下求出较好的结果。FROFI算法虽然能直接得到最优的结果，但需要的适应度评估次数也相应地大幅提高［13］。同样，IPES 算法也可以对大多数函数求取出最优值，但其所需的适应度评估次数也不少［14］。这对于目标函数较为复杂的情况来说会极大地增加计算成本。由此可见，本文所提出的SDECOA 能够在更少的适应度评估次数下求取较为精确的结果，极大减少了计算成本。

图1和图2分别给出了SDECOA、FROFI和IPES三种算法对于g04、g16 两个函数的收敛曲线。种群数设置为80，最大适应度评估次数设置为50 000。从图1～2 可看出，FROFI 和IPES 两种算法都在数千次以后才开始快速向最优值收敛，而SDECOA 则在千次以前就快速地向最优值收敛了。因此，SDECOA 在前期具有更快的收敛能力，具有较好的寻优效果。

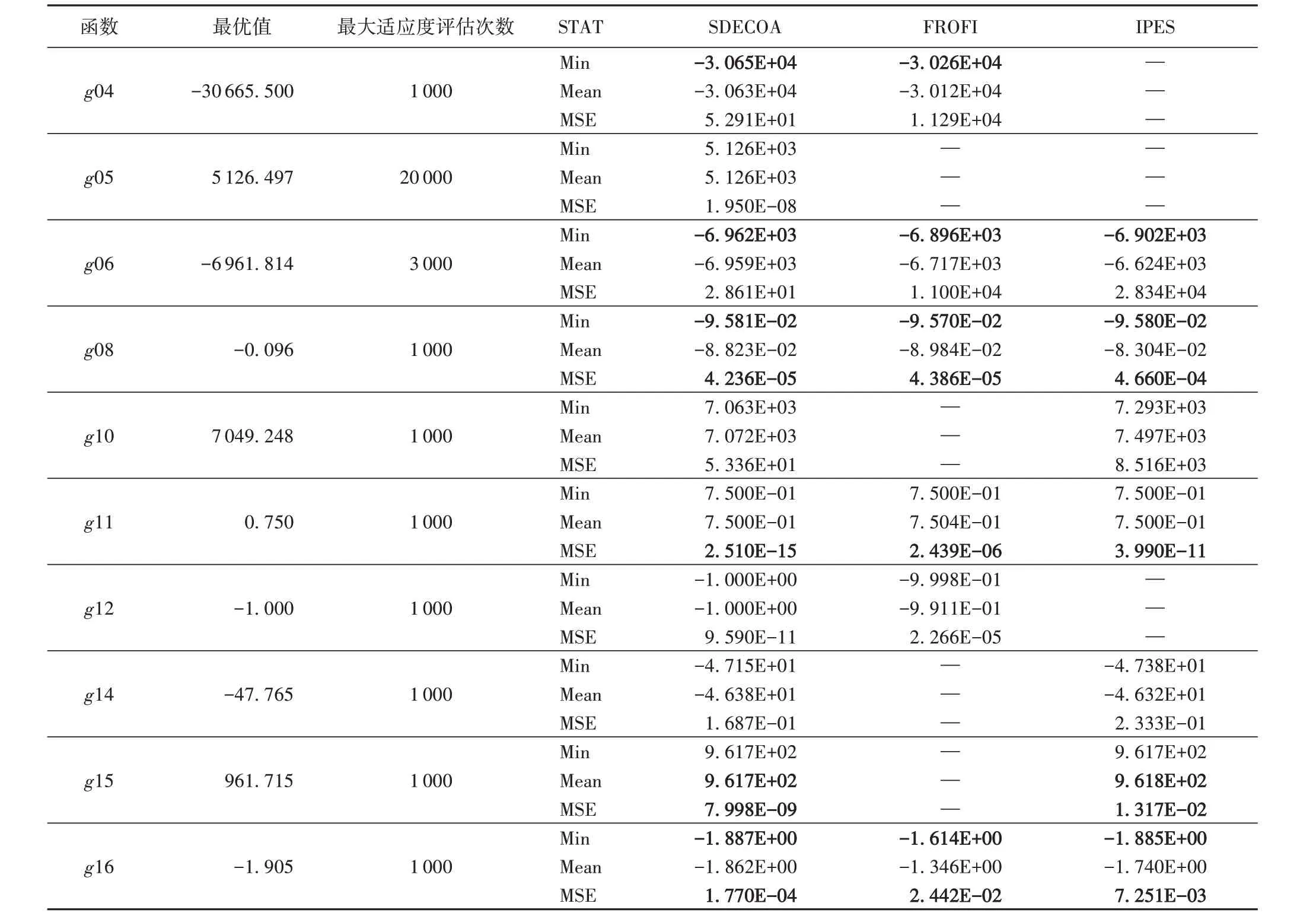
表1 三种优化算法在10个测试函数上的结果比较Tab. 1 Result comparison of three optimization algorithms on 10 test functions

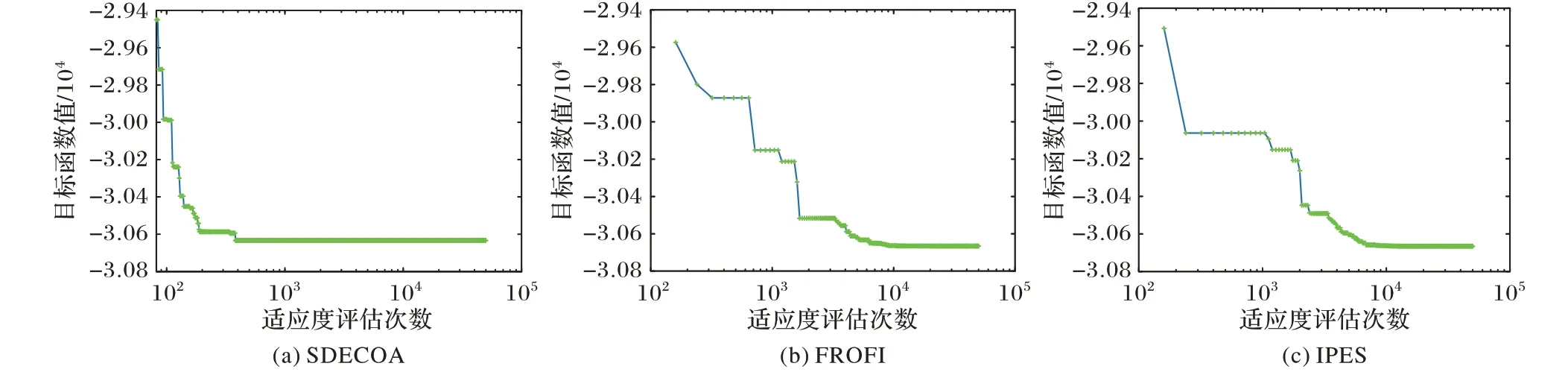
图1 对函数g04寻优过程中SDECOA、FROFI、IPES的收敛曲线Fig.1 Convergence curves of SDECOA，FROFI and IPES in the optimization process of function g04

图2 对函数g16寻优过程中，SDECOA、FROFI、IPES的收敛曲线Fig.2 Convergence curves of SDECOA，FROFI and IPES in the optimization process of function g16

3.2 不同代理模型的效果比较

现有的代理模型多种多样，本文将三种代理模型分别与算法相结合，通过比较运行20 次的结果及其方差来分析各个代理模型的优劣。本文所用的三种代理模型为:克里金模型（KRG）、多项式回归模型（PRS）、后向传播神经网络模型（BPNN）。实验结果如表2所示。

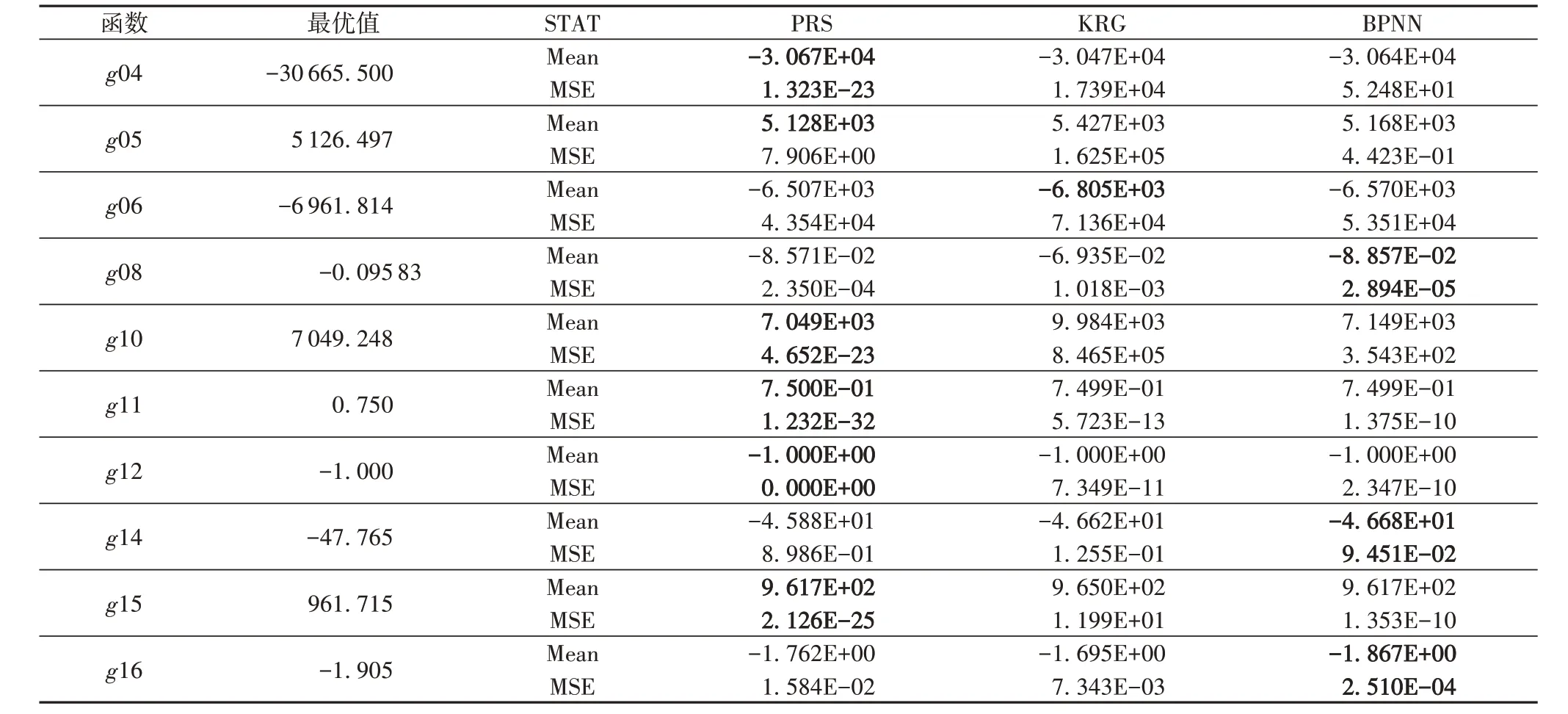
表2 三种代理模型的效果比较Tab. 2 Effect comparison of three surrogate models

从表2 中可以看出，三种代理模型对于不同的函数有着不同的效果:对于PRS 来说，它在g04、g05、g10、g11、g12、g15的表现最好，最为接近真实最优值且方差最小；对于KRG 来说，其仅在g06、g11、g12 的表现较好；对于BPNN 而言，它在g08、g14、g15、g16 等部分函数上有较好的表现。综上所述，PRS 对于在大部分测试函数都有着更好的表现，其次是BPNN，效果相对较差的则是KRG。

3.3 工字梁设计优化实例

工字梁设计优化问题［15］是如今比较典型的实际工程设计问题。

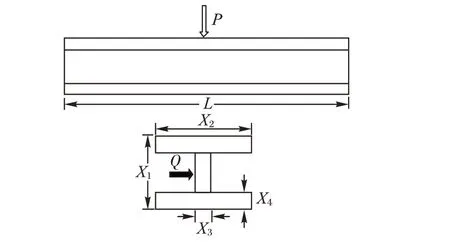
图3 工字梁设计问题Fig.3 I-beam design problem

本文通过对该问题的优化来体现SDECOA 的优化能力和效率。工字梁设计优化问题的目标是:给定荷载条件，使得在同时满足横截面和应力约束的条件下形变量最小。该问题的各项参数如下。

杨氏弹性模量:E = 2 × 104kΝ/cm2；

最大弯曲力:P = 600 kΝ，Q = 50 kΝ；

工字梁长度:L = 200 cm。

优化目标为最小化形变量:

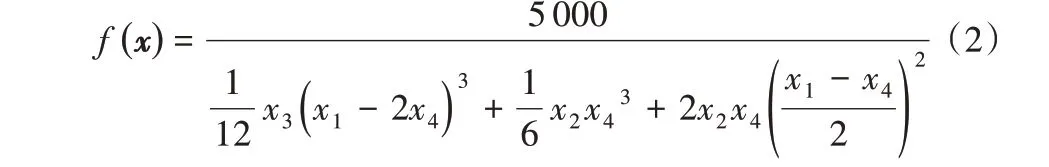
约束条件:

1）横截面积小于300 cm2。

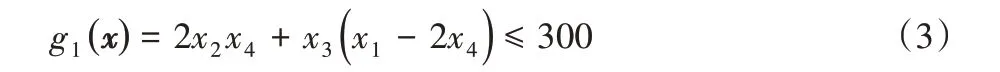
2）工字梁容许弯曲应力小于6 kΝ/cm2。

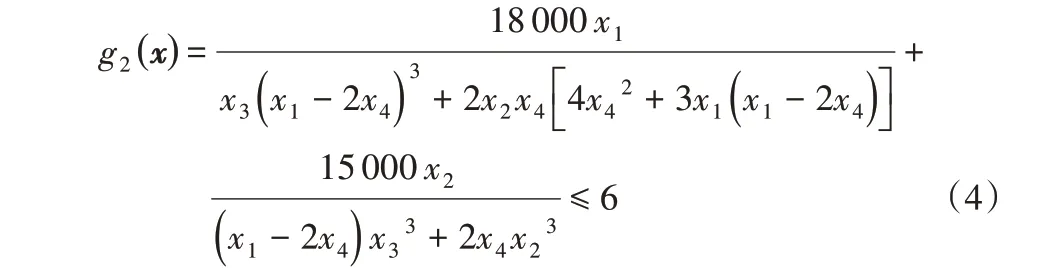
3）初始设计空间:10 ≤x1≤80，10 ≤x2≤50，0.9 ≤x3≤5，0.9 ≤x4≤5。

首先，采用拉丁超立方采样方法生成40 个初始设计变量，对每一个初始设计变量进行适应度评估并计算出对应的约束违反度值。再用后向传播神经网络模型（BPNN）对目标函数建立代理模型。最后程序运行结束得到的结果如表3所示。

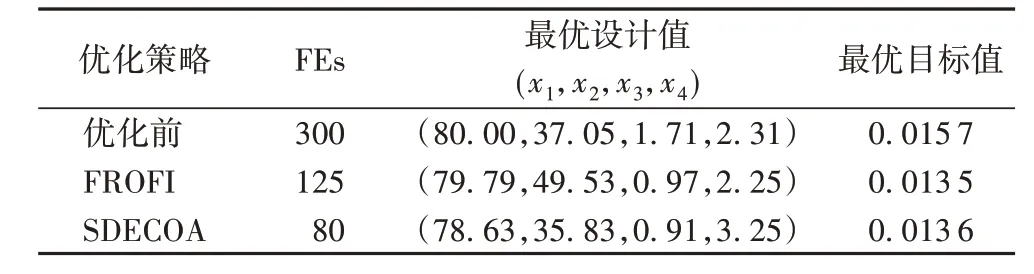
表3 SDECOA应用效果Tab. 3 Application effect of SDECOA

从表3 中可以看出，使用本文提出的SDECOA 比优化前以及采用FROFI 算法的模型调用次数都要少，而且优化精度也比优化前更高，但是略低于FROFI 算法。SDECOA 能在大幅减少模型调用次数的情况下获得较为精确的结果。所以，本文所提出的SDECOA 在解决复杂的约束优化问题时在优化效率方面具有一定的优势，能够有效提升优化的质量和效率。

4 结语

本文针对复杂约束优化问题提出了基于代理模型的差分进化约束优化算法，并且还将可行性法则与目标函数的信息相结合。该算法利用父代来建立真实目标函数的代理模型，在之后父代与子代的比较中，对于子代个体的评估通过代理模型来完成，当确定某一子代进入父代时，再对该子代使用真实目标函数进行评估。通过实验可以看出，SDECOA 能够在较少的适应度评估次数下获得更优的结果。使用不同的代理模型效果也不尽相同。总的来说，使用PRS 作为代理模型对于大多数测试函数都能取得最优的效果，而且，在对于10 个测试函数的实验中，相对于不使用代理模型的FROFI 和IPES这两种方法，SDECOA 能够更快地收敛向最优值，同时取得较好的结果。

但是，现有的代理模型是静态的代理模型，第一次建立后就不可更改。这可能不利于对原函数的拟合，从而影响优化效果，所以可以采用在优化过程中不断加入采样点的动态代理模型，进一步细化代理模型，可能会取得更好的优化效果。