基于加权正交约束非负矩阵分解的车脸识别算法

王锦凯，贾 旭

（辽宁工业大学电子与信息工程学院，辽宁锦州121001）

（∗通信作者电子邮箱wangjinkai@lnut.edu.cn）

0 引言

汽车数量的快速增长导致了套牌违法行为呈多发态势，许多交通卡口已增加摄像头对该违法行为加以监控，传统人工查看视频的方法因效率低下，已很难对违法行为作出及时处理，因此，提出一种有效的车脸识别算法，对套牌车辆进行自动检测是具有重要意义的。

车辆识别技术主要经历两个关键的阶段:1）传统的人工特征提取与分类方式；2）基于深度学习的识别方法［1］。最初颜色作为一种显著的车辆特征被广泛研究与分析，如不同空间的颜色直方图特征［2-3］；但由于车身颜色易受光照强度变化影响，研究人员将关注点转移到了车辆的全局、局部纹理特征［4］与形状特征［5］上，与此同时，一些经典的关键点特征也逐渐被应用在了车辆识别中，如尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）特征［6］、可变形部件模型（Deformable Parts Model，DPM）特征［7］等；而后，Boukerche等［8］将多种人工特征进行了融合，形成了多粒度特征，进一步提高了识别效果；此外，考虑到二维图像缺少深度信息，车辆的三维特征［9-10］也被更多的学者研究。近年来，深度学习因其可以自适应学习出有效的特征而被重视，研究人员也将多种深度学习模型应用到了车辆识别中［11-16］，当具有足够规模的训练样本时，基于深度学习的算法可以取得较好的效果。然而，目前车脸图像的数据集数量较少，限制了深度学习模型对于车脸图像的识别效果；此外，光照变化、局部遮挡等不合作因素又使得颜色、特征点等人工特征的有效性降低，这些都会给识别带来困难。

本文面对多类别且标注数量有限的车脸图像数据，对非负矩阵分解（Nonnegative Matrix Factorization，NMF）模型加以权重、稀疏与正交约束，自适应地建立出描述图像中若干关键区域的特征基，并通过特征基线性叠加对任意车脸图像作出准确描述，进而实现车脸的准确识别。

1 初始特征提取

车脸图像特征主要体现在车身颜色与局部区域形状上，但受光照变化影响，同一辆车在不同时间段采集时会出现一定的颜色偏差，如图1 所示，因此，基于颜色特征的识别算法的有效性将会降低，这里将更多关注图像的局部区域形状特征。

图1 不同光强下采集的车脸图像Fig.1 Vehicle face images acquired under different light intensities

在图像中，区域是由边缘围绕形成的，而图像边缘主要体现在具有方向性的高频信息上，如何准确描述这些具有方向性的高频信息将成为初始特征提取的关键。方向梯度直方图（Histogram of Oriented Gradients，HOG）特征是通过计算和统计图像局部区域的梯度方向而得到的，对边缘能够进行很好的描述［17］，因此，将HOG 特征作为车脸图像的初始特征是合理的。

首先，将基于YOLO（You Only Look Once）模型分割后的车脸图像大小归一化为N × N像素，如图2所示。

图2 归一化车脸图像Fig.2 Normalized vehicle face image

而后，对图像进行分块处理，每一块子图像大小为M × M像素，相邻块覆盖T 个像素宽度，因此，图像块的个数k 可由式（1）得到:

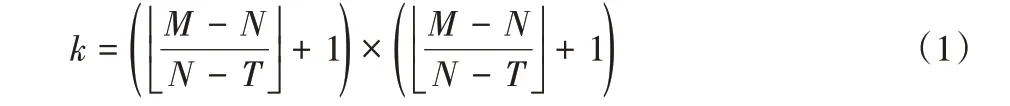
在计算梯度方向直方图时，选择s 个角度区间，从而可以得到车脸图像的初始特征Yi维度为n（n = k × s）。

2 特征降维与特征基的建立

对车脸图像进行初始特征提取后，需对其进行降维处理，目的是获得描述图像中若干关键区域的特征基。常用的特征降维方法有主成分分析（Principal Component Analysis，PCA）法、线性判别分析（Linear Discriminant Analysis，LDA）法等。分解后矩阵元素可以是正的，也可以是负的，从数学的角度考虑，负值是可以接受的；但对于图像处理问题，负值却缺乏实际意义，如在人脸识别中，人脸图像可以被认为是多幅特征基图像加权叠加得到的，这里的特征基图像像素值与权重值都不可能是负的。基于以上分析，本文将采用非负矩阵分解思想来实现特征降维与特征基建立［18］。即给定一个非负矩阵Y，可将其近似分解成两个非负矩阵U 与V 的乘积，如式（2）所示:

其中:Y 的列向量表示训练样本初始特征；U 的列向量表示特征基向量；V 的列向量表示分解系数，即新的特征。进而可获得目标函数，如式（3）所示:

非负矩阵分解可以较好地保证分解结果的物理特性，但并没有考虑对于分类识别的帮助性。因此，对非负矩阵分解模型进行了以下改进:1）根据区域重要性差异，对模型加以特征基加权约束；2）根据少数关键区域即可决定车辆类别的思想，对模型加以稀疏约束；3）基于类间差异性原理，对模型加以正交性约束。具体改进方法如下:

1）特征基加权约束。

车脸图像中，不同区域特征在识别时起的作用有所不同，如车辆标致与车脸栅格区域因其具有较好的独特性，在识别时发挥更为重要的作用；而车顶与引擎盖颜色区域变化较为平缓，特征的重要性有所降低。因此，在分解时，描述这些不同区域的基向量所占的权重也应不同，这里为不同的特征基分配不同的权重系数，目标函数可改进为式（4）:

其中:U为基向量矩阵；Z为权重矩阵；V为系数矩阵。

2）稀疏性约束。

车脸识别过程中，除了少量具有不同权重的特征外，通常有一些区域几乎不对识别产生作用与影响，如车辆背景区域、车窗区域等，即车脸特征应该具有较好的稀疏性。因此，需对系数矩阵Z 与V 加以稀疏性约束，从而目标函数可改进为式（5）:

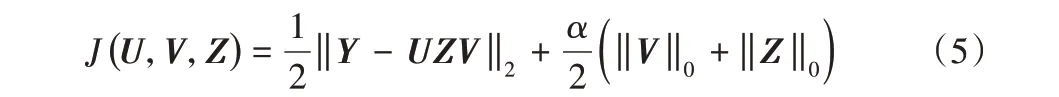
根据压缩感知理论，求解矩阵的0 范数为NP 难问题［19］，可将其等价于求解V的2范数，目标函数可改进为式（6）:

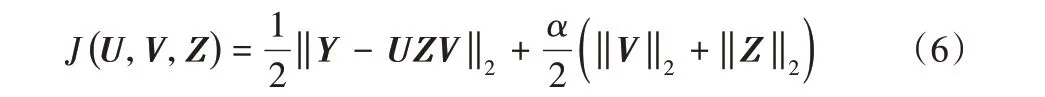
3）特征基正交性约束。为实现车脸特征的有效降维，即降低车脸特征基间的相关性，减少特征间的冗余，除对NMF进行加权性与稀疏性约束外，还应尽可能提高特征基间的正交性。基于以上分析，目标函数可进一步改进为式（7）:

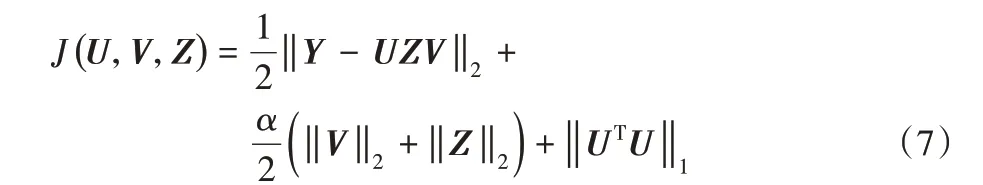
综上，最优分解结果通过式（8）求得:

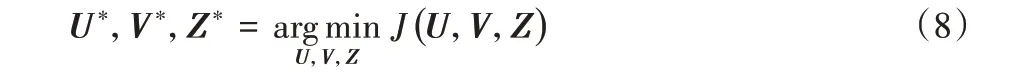
3 基于梯度下降的目标函数求解

经过变换，目标函数式（8）可以转化为式（9）:

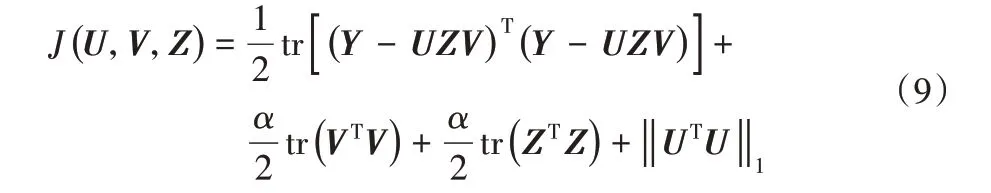
而后，分别求解目标函数式（9）对U、V 与Z 的偏导数，如式（10）～（12）所示:

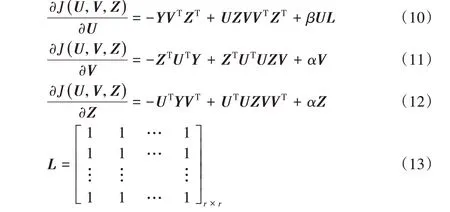
而后，给定U，V 与Z 的初始值，并将按照式（14）～（16）规则迭代，直至满足停止条件。

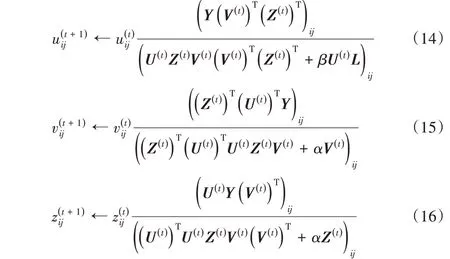
Step 3 如果d(Vi，Vj)＞g，两幅车脸图像表示同一类车；否则，两幅车脸图像表示不同类车。

4 收敛性证明

为证明求解最优参数过程中迭代的收敛性，需引入辅助函数。

定义1 如果式（17）成立，则定义G(h，h′)是F(h)的辅助函数。

引理1 如果G是辅助函数，则函数F在式（18）迭代更新规则是非增的。

的序列:

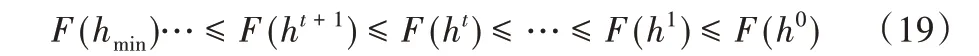
因此，通过定义辅助函数，可证明式（10）～（12）的收敛性。

对于目标函数式（7），假设U为独立变量，可得:

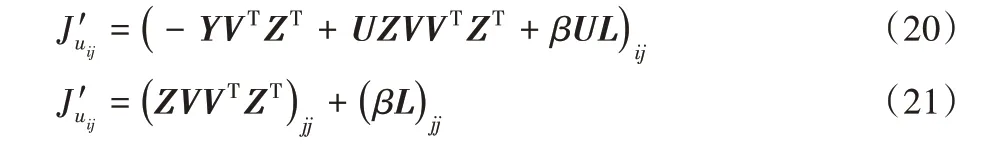
其中:F(u)= J(u)，0 ＜i ≤n，0 ＜j ≤r。

引理2 假设U 为独立变量时，可定义式（22）为辅助函数。

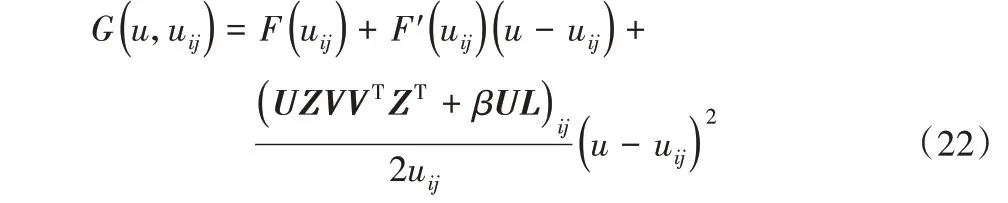
证明 容易得到G(u，u)= F(u)，只需证G(u，uij)≥F(uij)即可。

将式（7）进行泰勒级数展开，得到式（23）:

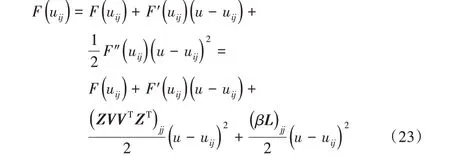
由于式（24）成立，

因此，引理2得证。

对于目标函数式（7），假设V为独立的变量，可得:

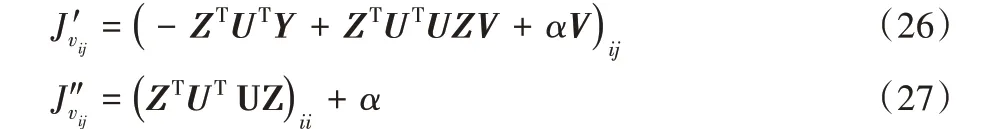
其中:F(v)= J(v)，0 ＜i ≤r，0 ＜j ≤m。

引理3 假设V 为独立变量时，可定义式（28）为辅助函数。

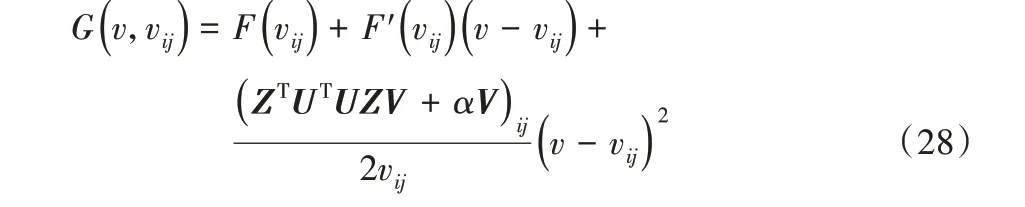
证明 容易得到G(v，v)= F(v)，只需证G(v，vij)≥F(vij)即可。

将目标函数（7）进行泰勒级数展开，得到式（29）:

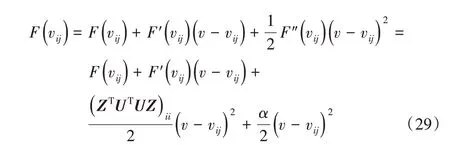
由于式（30）～（31）成立，

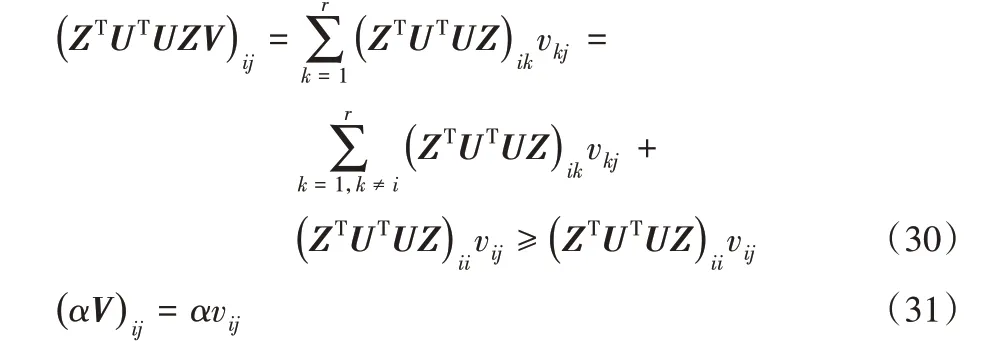
因此，引理3得证。

对于目标函数式（7），假设Z为独立的变量，可得:

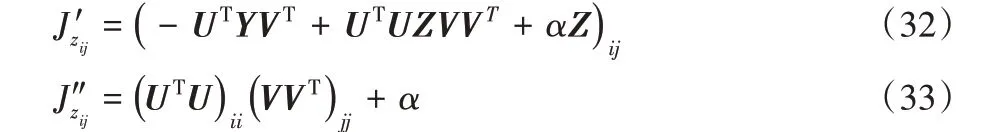
其中:F(z)= J(z)，0 ＜i ≤r，0 ＜j ≤m。

引理4 假设Z 为独立变量时，可定义式（34）为辅助函数。

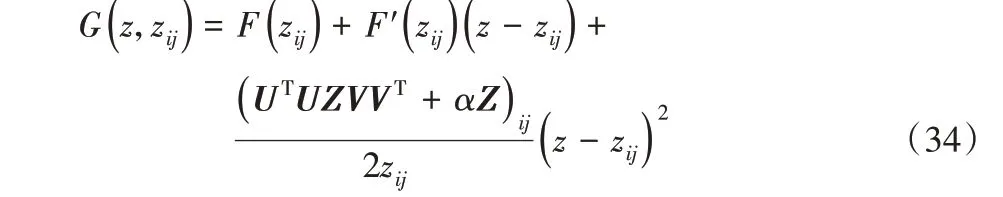
证明 容易得到G(z，z)= F(z)，只需证G(z，zij)≥F(zij)即可。

将目标函数（7）进行泰勒级数展开，得到式（35）:

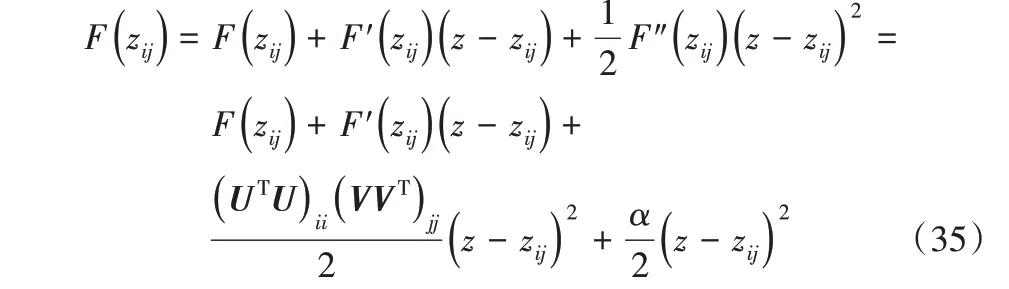
由于式（36）～（37）成立，

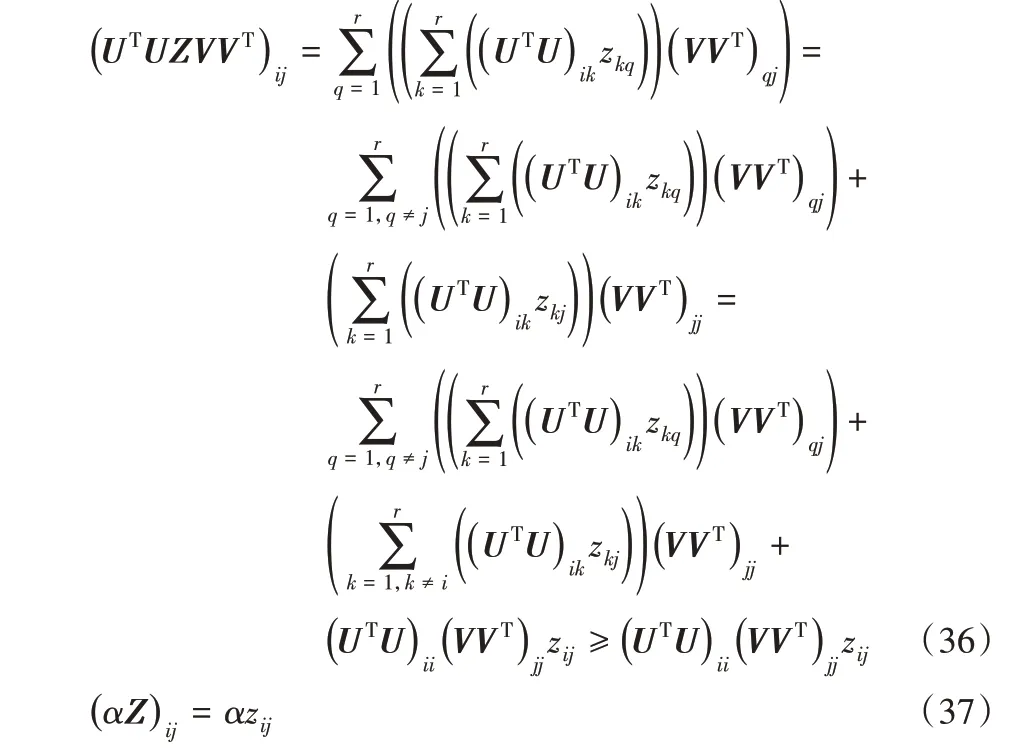
因此，引理4得证。

综上，可得出迭代过程是收敛的。

5 实验与结果分析

5.1 数据集

实验采用了两个数据集:1）某省22 个交通卡口处监控摄像头采集的车辆图像作为实验数据集，共103 028 幅图像，其中部分样本如图3（a）所示；2）BITVehicle 数据集，共9 852 幅图像，部分样本如图3（b）所示。

图3 数据集中部分样本Fig.3 Some samples in datasets

5.2 算法参数设定

本文提出的NMF 模型参数一部分依据经验设定，另一部分依据实验所得。其中，依据经验设定的参数如下:

1）初始特征参数设定。

车脸区域分割后，将其归一化至256 × 256 像素；经过分块后，每一块子图像大小为32 × 32 像素，相邻块重叠16 个像素宽度；在利用HOG 算子计算梯度方向直方图时，角度区间数目设为8。

2）NMF模型参数设定。

选取500 个不同类别车辆的车脸图像进行训练，即在目标函数中，Y 的列数为500；求解U∗、V∗、Z∗时的最大迭代次数nmax= 20 000。

设定经验参数后，需依据实验对其他参数进行优化。

1）NMF模型参数优化。

模型中共有3 个参数需进行优化，分别为降维后特征维数r，平衡因子α 与β。这里，令平衡因子α 与β 的取值分别为1、0.1、0.01；特征维数的取值分别为原特征维数的20%至70%。实验过程中，采用最近邻分类器对3 000对车脸图像进行比对测试，并利用错误接受率（False Acceptance Rate，FAR）与错误拒绝率（False Reject Rate，FRR）作为衡量识别效果的标准。

当采用不同模型参数时，实验结果如图4 所示，从中可看出:当降维后特征维数r = 0.4n，平衡因子α = 0.1，β = 1 时，可获得最优的识别性能。

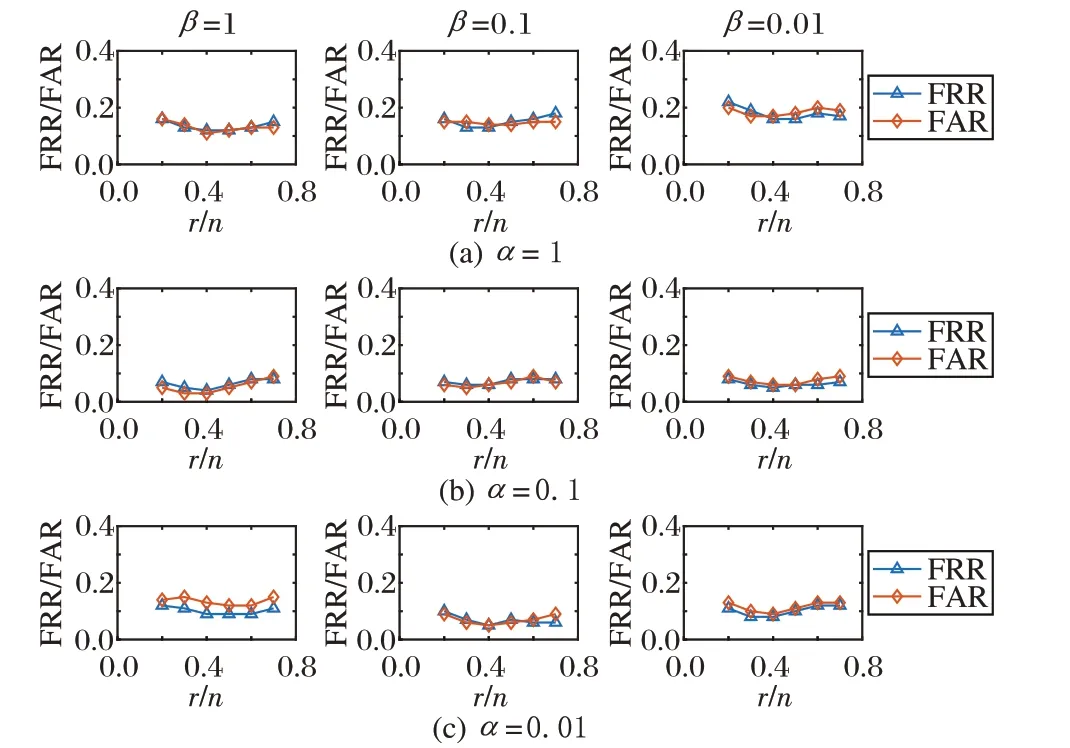
图4 不同参数下车脸识别性能比较Fig.4 Comparison of vehicle face recognition performance under different parameters

2）识别算法参数。

车脸识别时，仅涉及一个参数，即特征相似性阈值g。这里，通过不断调整阈值，对3 000对车脸图像进行测试，并利用真实接受率（Genuine Accept Rate，GAR）与FAR 作为衡量识别效果的标准，测试结果如图5所示。

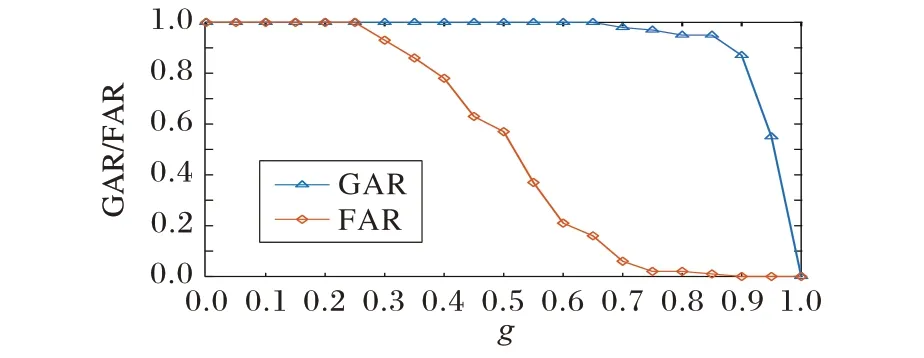
图5 不同阈值条件下车脸识别性能变化Fig.5 Vehicle face recognition performance variation under different thresholds

根据式（38），获取最优阈值g∗= 0.85。

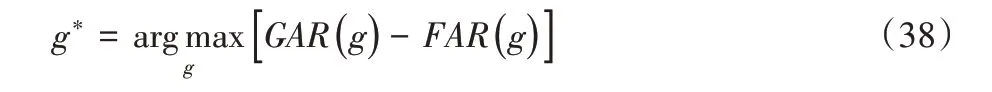
5.3 算法测试结果

确定了特征基向量与算法参数后，分别采用5 246对正样本和5 000对负样本对本文算法进行测试，其中测试样本中包括光照变化、尺度变化等因素。首先，基于第3 章中的识别算法对图像进行分解，获得新的特征向量；而后，分别求取每一对测试样本新特征间的相似性值，并与式（38）获得的阈值g∗进行比较，获得识别结果，如表1所示。

表1 实验结果统计Tab.1 Statistics of experimental results

表1中:TP（True Positives）为正例且被分类器划分为正例的样本对数；FP（False Positives）为负例但被分类器划分为正例的样本对数；FN（False Negatives）为负例但被分类器划分为负例的样本对数；TN（True Negatives）为正例且被分类器划分为负例的样本对数。部分识别结果如图6所示。

图6 部分车脸匹配结果Fig.6 Some vehicle face matching results

准确率计算如式（39）所示。由实验结果可以看出，本文算法的准确率Acc可达97.56%。

5.4 算法比较与分析

分别将本文算法与传统算法和深度学习算法进行比较。其中，传统算法包括基于颜色特征［3］、SIFT 特征［6］、多粒度特征［8］的识别算法；而深度学习算法包括基于CNN模型［11］、受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）模型［14］、迁移学习模型［16］的识别算法。实验过程中，仍采用5.3 节中5 246 对正样本和5 000 对负样本对算法进行测试，实验结果如图7所示。

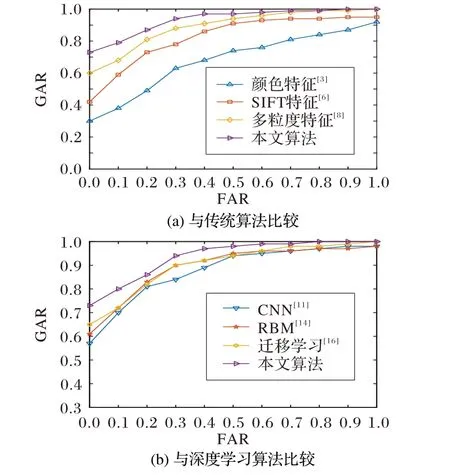
图7 不同识别算法的实验结果比较Fig.7 Experimental result comparison of different recognition algorithms

由图7（a）可以看出，本文算法性能要优于其他传统车辆识别算法，主要有以下原因:由于白天和黑夜的光照强度差异很大，导致同一颜色车辆在不同时段采集图像中出现明显的颜色差异，如图1 所示，从而使基于颜色特征的识别算法有效性降低，而在本文算法中，虽然车脸图像因光照变化会出现一定的颜色差异，但描述边缘的高频信息并不会因此而发生较大改变，从而降低了光照变化对于识别的影响，此外，边缘高频信息的方向性保证了车脸不同区域间的色差，这也间接描述了车脸图像的颜色特征，可以较好地避免对不同颜色的同类车型的错误识别，如图8（a）；而对于曝光较强的或颜色单一的车脸图像，如图8（b），可提取的SIFT 特征点数量有限，给识别带来较少的依据，从而降低了识别的准确率；基于多粒度特征的识别算法提取了整体车辆多个区域的特征，而针对车脸图像的特征相对较少，算法在整体车辆识别上可以取得较好的效果，但对于车脸区域的识别有效性降低。而由图7（b）同样可以看到本文算法的优势，其主要原因在于整体车辆图像的数据集较为丰富，可获得大量训练样本，因此训练后的模型可取得较高的正确识别率；而目前关于车脸图像的数据集相对较少，自建的数据集训练样本数量有限，容易导致训练后模型出现过拟合现象，从而降低模型的识别效果。

图8 多种条件下采集的车脸图像Fig.8 Vehicle face images acquired under various conditions

以上实验是在PC 上运行的，其中处理器为Intel Core i5-4460 CPU 3.2 GHz，内 存16 GB，GPU 显 卡 型 号 为NVIDIA Geforce 1080Ti。其中，传统识别算法在Matlab 2017b 环境下运行的，而基于深度学习的识别算法是在Python 2.7 环境下运行，运行时间如表2所示。

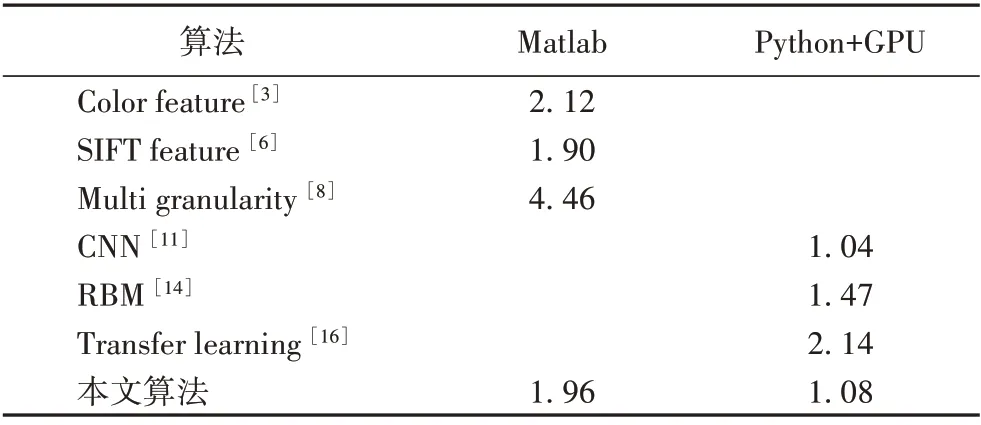
表2 识别时间对比结果 单位：sTab.2 Comparison result of recognition time unit:s

通过不同运行环境下的实验，可以看出本文算法的识别速度略优于基于颜色特征与RBM 的识别算法，明显好于基于多粒度特征与迁移学习的识别算法，而与基于SIFT 特征与CNN 的识别算法基本一致，并且Python 环境下1.08 s 的识别时间基本能够满足识别的实时性要求。

6 结语

为提高套牌车辆检测效率，本文提出了一种有效的车脸图像识别算法，即对NMF 模型加以多权重、稀疏性、正交性约束，在对车脸特征实现降维的同时，使其更有利于车脸图像的正确识别。通过实验验证，在对样本进行少量标注的前提下，本文算法可以获得较高的正确识别率，并对光照强度变化具有较好的鲁棒性。在取得一定效果的同时，仍存在一些问题有待解决，如实验的数据集还需进一步丰富，以验证算法的普适性。