基于焦点损失的半监督高光谱图像分类

张凯琳，阎 庆*，夏 懿，章 军，丁 云

（1. 安徽大学电气工程与自动化学院，合肥230601；2. 测绘遥感信息工程国家重点实验室（武汉大学），武汉430079）

（∗通信作者电子邮箱*rubby_yan5996@sina.com）

0 引言

高光谱图像（HyperSpectral Image，HSI）［1］包含数百个连续的窄光谱带，跨越可见光到红外光谱波段，光谱信息丰富，因此在诸如遥感数据分析［2］、土地覆盖分类［3］、城市区域的检测［4］和环境科学［5］等许多应用中发挥了至关重要的作用，其中高光谱分类问题［6］受到了学术界的极大关注。近年来深度学习方法在计算机视觉和图像处理等领域取得了较好的效果［7-8］，与传统机器学习相比具有表达能力强、适合处理大数据等优点，已经广泛应用于高光谱图像分类领域中。基于深度学习的高光谱图像分类方法主要可以分为无监督、监督和半监督三种类型。无监督分类算法仅利用未标记数据来传达数据内在信息，完成分类。例如堆叠自编码器［9］和深度置信网络［10］已被用于从高光谱数据中提取深度特征。相对于传统机器学习，无监督方法无需训练过程，可以直接利用数据进行建模分析；然而，由于缺乏先验知识，无监督方法的效果受到了一定的限制。

监督分类方法通过利用类标签的先验知识，建立分类判别规则来完成分类任务。在监督分类方法中，深度卷积神经网络（Convolutional Neural Network，CNN）［11］在光谱域中对高光谱图像进行分类。和传统机器学习方法相比，CNN 不需要人工构造特征，而且还具有一定的自学习能力，能够从训练数据中学习到高度代表性的图像特征；但CNN 只利用了光谱信息，对空间特征的关注不足。针对这些不足，近年来也有很多学者进行了相应的改进。如三维卷积神经网络（3D CNN，3D-CNN）［12］和双通道卷积神经网络（Dual-Channel CNN，DCCNN）［13］结合了空间信息和光谱信息，实现了“光谱合一”，与传统的CNN 相比无论是视觉效果还是数值分析结果都取得了较大提升。循环神经网络（Recurrent Neural Network，RNN）［14］把高光谱像素视为序列信息，然后通过网络预测每个样本的类别，可以有效地处理高光谱数据并减少参数总数，对比其他算法获得了更高的准确度。

与传统机器学习基于手工特征提取的方法不同，深度神经网络以端到端的方式执行高光谱图像的分类。为了执行端到端的分类，这些基于深度学习的方法需要在训练期间利用大量标记样本来学习参数。监督分类算法借助于大量训练信息的指导，所以分类精度比较高，因此在很多领域被广泛使用，但是其效果在很大程度上取决于标记样本的数量和质量。然而，众所周知，对于高光谱图像而言，对样本的标记工作非常困难且代价高昂，因此可利用的训练样本数量非常有限。而这正是利用监督分类方法实现高光谱图像分类的难以克服的障碍之一。为了解决这个问题，一些学者提出了半监督深度学习方法［15-16］。半监督方法是通过利用有限的标记样本和大量未标记的样本来减轻“小样本问题”。半监督算法不仅可以利用标记样本传递的有限监督信息，而且充分考虑到高光谱图像中未标记样本提供的丰富信息，从而既克服了无监督算法的低精度又缓解了监督算法中对训练样本的过分依赖、忽视了非标记样本在分类任务中的巨大价值的问题，对分类性能的改善具有重要的意义。例如，李绣心等［17］构造了一种能同步处理带标签和未带标签数据的卷积神经网络，同时将交叉熵损失函数和K-means 聚类算法结合起来，进而提高了分类性能；Kipf等［18］提出了一种基于图的半监督学习方法，该方法能够以图作为输入，可以学习到隐藏层的特征，从而达到较好的效果；Ma等［19］提出了一种基于多决策标注和深度特征学习的半监督分类方法，以利用尽可能多的信息来实现分类任务；Wu 等［16］提出了一种通过基于Dirichlet 过程的聚类方法——C-DPMM，首先利用该聚类算法获得所有样本的伪标签，再利用这些伪标签对网络进行预训练，最后使用标记样本对网络进行精调。Wu方法［16］利用了大量未标记的数据，实现了参数的初始化并且可以有效防止过拟合。然而，该算法仍然有两个缺点:首先，该算法中使用的基于C-DPMM 的聚类方法无法捕获高光谱图像的稀疏特征。高光谱图像是一种高维数据，基于稀疏的方法在处理高光谱图像方面［20-21］已经表现出较大的优势。例如，Yan 等［20］提出了通过使用已知的监督信息来估计未标记样本的类概率，然后将类概率引入到稀疏子空间聚类（Sparse Subspace Clustering，SSC）模型中，以获得更准确的稀疏表示系数矩阵，从而可以获得更好的聚类结果。其次，因为高光谱图像的样本分布存在不平衡的问题，Wu等［16］所采用的交叉熵损失函数不能充分掌握高光谱样本的分布不平衡的状况，也严重制约了高光谱数据分类精度的进一步提高。

在深度学习领域，对目标函数的改进也是一个引人关注的课题。Wen 等［22］通过将交叉熵损失与中心损失结合起来，使学习的特征具有更好的泛化能力以及判别能力；Liu等［23］利用广义大边缘交叉熵损失（L-Softmax），可以让学习的特征更加清晰；Lin 等［24］提出了通过焦点损失（Focal Loss）来解决分类问题中数据类别不平衡以及判别难易程度差别的问题。

最后，值得注意的是，高光谱图像分类的大多数算法只关注光谱特征，而对分类任务同样重要的空间特征往往被忽视了。马尔可夫随机场（Markov Random Fields，MRF）可以将光谱信息与空间信息相结合，鼓励相邻像素具有相同的类别标签［25］，已被验证可以显著提高高光谱图像的分类精度［26］。

基于文献［16，24］方法，本文提出了一种新的基于焦点损失的半监督判别卷积神经网络的算法。考虑到高光谱图像的稀疏性，本文选择用稀疏子空间聚类（SSC）代替基于Dirichlet的算法（C-DPMM）来实现聚类。稀疏子空间聚类是一种基于稀疏表达的优秀聚类方法，在人脸聚类［27］、运动分割［28］都有广泛的应用。此外，引入了基于焦点损失的目标函数来解决分类问题中数据分类难度差异的问题，以此来提高分类性能。最后，本文比较了两个框架的效果，其中一个框架将马尔可夫随机场作为图像后处理，而另一个框架没有进行后处理，以此分析马尔可夫随机场在分类任务中的效果。

1 相关工作

1.1 稀疏子空间聚类

稀疏子空间聚类（SSC）是一种将稀疏表示（Sparse Representation，SR）引入到子空间聚类中的方法，为子空间聚类提供了一种新的模式，已成功应用于人脸识别［29］、运动分割［30］和图像分割［31］。稀疏子空间聚类是基于谱聚类的子空间聚类方法。通常，高维数据属于某个低维子空间，因此可以在低维子空间中被线性表示。稀疏子空间聚类的基本思想是数据的自表达属性，即子空间集合中的每个数据点可以有效地被表示为来自同一子空间的其他样本点的线性组合。因此，SSC 模型利用数据的自表达性来构建稀疏表示模型，如式（1）所示:

其中:C的第i列向量是样本yi的稀疏表示；diag(C) = 0是C的对角元素；E 是误差矩阵；λ 是稀疏系数和噪声矩阵之间的权衡参数。进一步，通过式（2）实现系数C的归一化:

根据归一化后的稀疏系数C 构建相似性矩阵，其中Q 是对称非负相似性矩阵。

最后，将谱聚类应用于相似矩阵Q，并获得数据的聚类结果。

1.2 卷积神经网络

卷积神经网络（CNN）在许多应用中都发挥着重要的作用，例如目标跟踪［32］、遥感成像［33］、行为识别［34］等。它是由卷积层（Convolution layer）、池化层（Pooling layer）、全连接层（Fully connected layer）组成。本文使用的卷积神经网络结构如图1所示。

在高光谱图像分类任务中，每个样本是大小为k × k × d的三维块，其中k × k是空间维度中的块的大小，d是高光谱数据的波段数。在将样本块传送到输入层之前，样本块是三维向量。

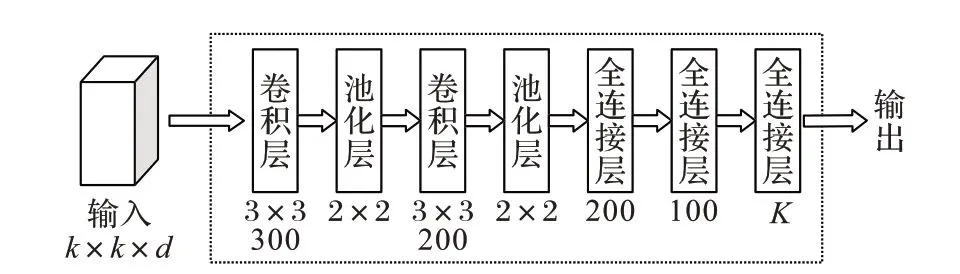
图1 卷积神经网络结构Fig. 1 Structure of CNN

1.3 焦点损失函数

目前目标检测的框架一般分为两种:基于候选区域的两阶段的检测框架［35］和基于回归的单阶段的检测框架［36］。相对于两阶段的方法，单阶段的方法具有快速、简单的特点，但是其准确率会差一些。Lin 等［24］认为是大量背景信息淹没了重要信息，即简单样本引导了梯度下降的方向导致了这个结果。于是Lin 等［24］提出了一种新的损失函数，即焦点损失来解决这一问题。

对于二分类的交叉熵损失（Cross Entropy，CE）函数，可以表示为:

其中:y ∈{± 1}表示数据的真实标签；p是y = 1时的类估计概率。在二分类中样本标签y = 1和y = -1是互斥的，因此引入一个分段变量pt，表示为:

所以，二分类的交叉熵损失就可以表示为:

CE(p，y) = CE(pt)= -log(pt) （6）

针对样本不平衡问题中产生的不同样本分类难度差异问题，Lin 等［24］对损失函数的形式进行了改进，降低易分样本的权重并专注于训练难分样本。因此引入了超参数γ，它表示难易样本权重差别的难度，γ 越大，差别也就越大，于是将焦点损失函数定义为:

针对数据集样本不均衡的问题，又引入一个权重参数α ∈[0，1]，为了标记方便引入一个分段变量αt，αt可以表示为:

简单地对正负样本的损失进行加权，αt平衡了正负样本的重要性。所以α-平衡焦点损失定义为:

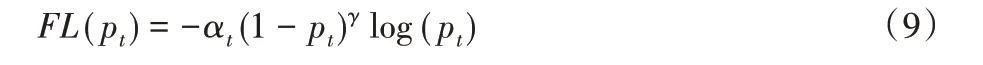
2 基于焦点损失的半监督深度学习框架

2.1 半监督学习框架

本文提出的半监督深度学习框架的结构如图2 所示。标记数据表示为{XL，YL}，其中YL是XL的标签，未标记的数据表示为XU。对于全部数据X，表示为{XL，XU}，X 的伪标签Z 可以由稀疏子空间聚类（SSC）生成。本文算法的流程如下:

1）由稀疏子空间聚类生成X的伪标签Z；

2）引入焦点损失函数代替交叉熵损失函数构造预训练卷积神经网络，称为CNN1，并利用{X，Z}完成CNN1的训练；

3）在CNN1的基础上构建新的卷积神经网络CNN2；

4）使用带标记的数据{XL，YL}来训练CNN2 中的全连接层和分类层，这一步称为微调；

5）将分类得到的结果，利用将马尔可夫随机场作为图像后处理，以此分析马尔可夫随机场在分类任务中的效果。

图2 本文半监督深度学习框架的结构Fig. 2 Structure of the proposed semi-supervised deep learning framework

在高光谱样本标记困难的背景下，用全部样本及其伪标签训练CNN1 可以充分利用大量未标记数据实现对网络的预训练。虽然这些伪标签不能提供确切的监督信息，但它们与真实地物标签具有一定的一致性。因此，可以通过CNN1 提取的特征来获得对精确分类有利的判别信息。

预训练和微调阶段网络模型如图3 所示。其中CNN2 保持与CNN1 相同的体系结构和参数，在去除焦点损失分类层后加入了全连接层和交叉熵分类层。通过引入焦点损失函数，使数据集样本不均衡和训练困难的问题得到改善。

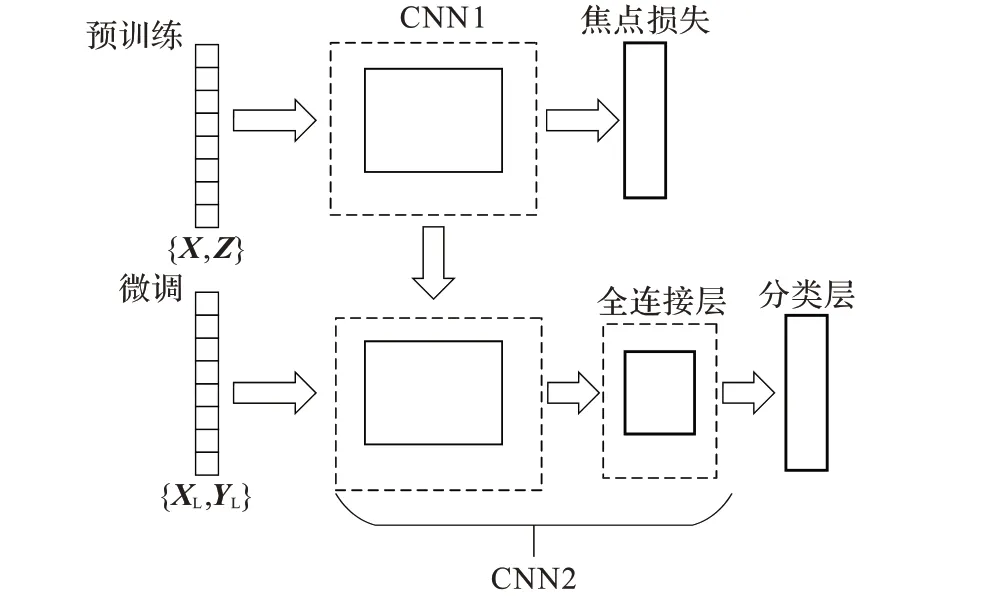
图3 预训练和微调阶段的框架Fig. 3 Framework of pre-training and fine-tuning stages

2.2 焦点损失用于多分类

对于多分类的问题，可以直接将交叉熵损失函数推广为多分类的形式。多分类的交叉熵损失函数如下所示:

其中:pi表示的是第i 个样本经激活函数后得到的概率；yi表示的是第i个样本真实标签。

交叉熵损失函数只对真实标签所对应的某一个单类进行相应计算，无法克服因数据集样本分布不均衡产生的分类难度差异的问题。而高光谱分类问题很明显是一个多分类的问题，因此受到二分类中焦点损失函数可以克服样本分类难度差异的启发，本文在多分类的任务中也引入了焦点损失。其中n表示的是类别数。多分类的焦点损失可以表示为:

焦点损失在多分类任务中的原理:

1）当一个样本被误分类时，则pi的值很小，调制因子(1-pi)接近1，损失不被影响；当一个样本被分得比较好时，则pi趋近于1，(1- pi)接近0，那么分得比较好的样本的权值就被调低了。

2）超参数γ 平滑地调节了易分样本调低权值的比例。增大超参数γ 能增强调制因子的影响。调制因子减少了易分样本的损失贡献，拓宽了样例接收到低损失的范围。

由以上分析可知，焦点损失函数中降低了易分样本的权重而增大了难分的易错样本的权重；因此在训练中更加关注到难分样本的贡献，从而解决了数据样本不均衡数据集难以训练的问题，可以进一步提高分类精度。

3 实验与结果分析

为了验证本文算法在不同情景中的有效性，在两个真实的高光谱图像数据集上进行了实验。使用以下三个评价指标对性能进行评估:总体准确度（Overall Accuracy，OA）、平均准确度（Average Accuracy，AA）和卡帕（Kappa）系数。OA 表示正确分类的样本的数量占所有样本的比例；AA表示各个类别分类精度的平均值；Kappa 用来度量分类结果与真实地表的一致程度。以上三个评价指标的值越大，说明分类性能越好。

3.1 实验数据描述

本文实验采用两个数据集:

1）Indian Pines 数据集，由机载可见光/红外成像光谱仪AVIRIS（Airborne Visible Infrared Imaging Spectrometer）传感器收集。该数据集有145× 145 像素，220 个光谱波段。实验选择了75× 82 × 220 子集，其中包含6 个类别的地物标签。其伪彩色图和真实地物图如图4所示。

图4 Indian Pines数据集的部分图例Fig.4 Subset of Indian Pines dataset

2）Pavia University 数据集，由反射式成像光谱仪ROSIS（Reflection Optics System Imaging Spectrometer）传感器获得。该数据集有610 × 340 像素和103 个波段。在本文实验中，选择了170 × 160 × 103 子集，其中包含9 类地物标签。其伪彩色图和真实地物图如图5所示。

将本文算法与CNN 和半监督卷积神经网络（Semi-Supervised CNN，SS-CNN）算法在上述两个数据集中进行了比较。CNN算法是一种比较常见的应用于高光谱图像分类的算法，它只考虑了高光谱的空间信息。SS-CNN 算法同样是将半监督的卷积神经网络算法与稀疏子空间聚类相结合，充分考虑到未标记的数据对高光谱图像分类的贡献，但SS-CNN算法在预训练阶段的损失函数为交叉熵损失函数。在SS-CNN 的基础上，本文提出了基于焦点损失的半监督卷积神经网络（Semi-Supervised Focal loss CNN，SSF-CNN）。通过对这两种半监督方法的对比可以验证本文在损失函数方面改进的有效性。最后为了分析马尔可夫随机场在分类任务中的效果，本文就是否对分类结果采用马尔可夫链进行后处理进行了一组对比实验。

图5 Pavia University的部分图例Fig.5 Subset of Pavia University dataset

3.2 Indian Pines数据集上的实验分析

为了在有限的训练样本的情况下评估所提出的方法，对于Indian Pines 数据集，从数据集的每个类别中随机选择10%的样本用于训练，其余的用作测试。在该数据集上采用不同方法得到的结果如图6所示。从图6的视觉效果中可以看出:本文SSF-CNN 算法表现出更好的分类效果，而CNN 和SSCNN 方法存在明显的误分，比如很多Corn-notill 类的样本被误分为Soybean-mintill类。此外，进一步采用马尔可夫随机场针对分类结果进行了后处理。因为马尔可夫随机场充分利用了样本的空间相关性，促进相邻样本被分为同一类别。因此这种网络框架，通过卷积神经网络充分利用高光谱样本的光谱相关性的同时又考虑到样本的空间相关性，实现了“光谱合一”的效果。从图6 可以看出，其分类的视觉效果得到明显的提升，进一步减少了误分和椒盐噪声的存在。

在表1 中给出了数据的定量分析。表1 的结果进一步验证了从图6 得出的结论，与CNN 相比，SSF-CNN 算法的OA、AA、Kappa 分别提高了2.5个百分点，5.52个百分点和3.46个百分点；与同是半监督框架的SS-CNN 相比，OA、AA、Kappa 也分别提高了1.17 个百分点、1.89 个百分点和1.61 个百分点。而当采用马尔可夫随机场作为分类后处理后，本文SSF-CNNMRF 算法取得了更好的分类结果，在6 个类别上的分类精度都 最 高，分 别 达 到95.12%、98.32%、99.78%、99.70%、98.29%和100%。就总体分类评价指标而言，SSF-CNN-MRF算 法 的OA、AA 和Kappa 分 别 达 到98.73%、98.54% 和98.24%。可以看出，在分类任务中马尔可夫随机场作为图像后处理是有益的，这是因为马尔可夫随机场侧重于高光谱图像的空间信息，并与卷积神经网络提取的光谱信息相结合，进一步提高了分类性能。

表1 Indian Pines数据集上不同方法的分类精度和运行时间对比Tab. 1 Comparison of classification accuracy and running time of different methods on Indian Pines dataset

图6 在Indian Pines数据集上的不同方法获得的分类图和后处理图Fig.6 Classification and post-processing images obtained by different methods on Indian Pines dataset

3.3 Pavia University数据集上的实验分析

对于Pavia University 数据集，本文从每个类别中随机选择了40 个样本进行训练，其余的样本用作测试。实验结果如图7 所示。和上述实验结论类似，图7 表明本文提出的SSFCNN 和SSF-CNN-MRF 算法分别取得到了最优的分类结果。进一步观察可以发现，CNN 和SS-CNN 都较多地将Self-Blocking 类和Bitumen 类误分为Gravel，而本文算法则明显减少了这种误分的发生。

与Indian Pines数据集上的实验类似，马尔可夫随机场作为图像后处理可以进一步提高分类精度。表2 中给出了实验结果的定量分析。由表2 可以发现，与CNN 相比，SS-CNN 和SSF-CNN 的OA分别增加1.77个百分点和2.61个百分点。这是因为SS-CNN 和SSF-CNN 不仅利用了标记的样本，还使用了未标记的样本以增加可用的训练信息。当使用马尔可夫随机场作为图像后处理时，Pavia University 数据集的分类效果得到了显著的提升；与没有使用马尔可夫随机场作为图像后处理相比，CNN-MRF、SS-CNN-MRF 和SSF-CNN-MRF 的结果表明，OA 的增加分别为1.63个百分点、0.77个百分点和1.08个百分点，表明了马尔可夫随机场在提高分类准确性方面起着重要作用。由于高光谱地物复杂且具有不同的数据结构，SSF-CNN-MRF 算法在分类过程中无法保证每一种地物的分类效果都很好，但是基于本文提出的半监督框架的SSF-CNNMRF 算法在三个总体性能指标OA、AA 和Kappa 上都是最高的。

图7 在Pavia University数据集上的不同方法获得的分类图和后处理图Fig.7 Classification and post-processing images obtained by different methods on Pavia University dataset

3.4 超参数γ的选取过程

在SSF-CNN 和SSF-CNN-MRF 算法中有一个重要超参数γ，在本节中，分别在上述两个数据集上进行的实验，来选取效果最优的超参数γ。实验结果如图8所示。

在图8中可以观察到，对于上述两个数据集，OA和γ之间的关系不是线性的，OA不是随着γ的增加而增加。当γ值为2时，在两个数据集上都获得了最佳的分类结果。同时，可以观察到，无论是否使用马尔可夫随机场作为图像后处理，超参数γ 的变化趋势都是相似的。此外，使用马尔可夫随机场作为图像后处理时，两个数据集上的SSF-CNN-MRF算法的分类结果都得到显着改善，再次表明马尔可夫随机场对于提高分类结果是十分重要的。

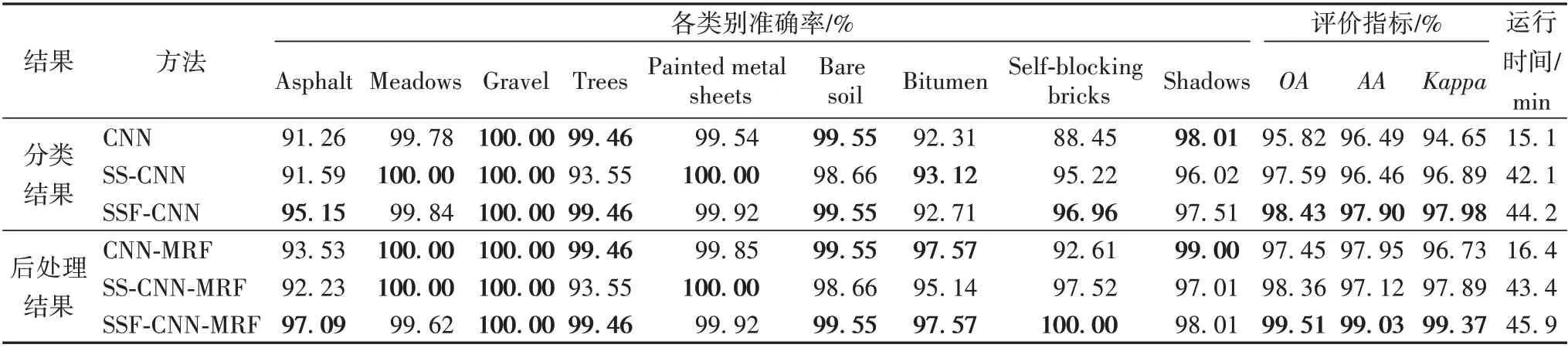
表2 Pavia University数据集上不同方法的分类精度和运行时间对比Tab. 2 Comparison of classification accuracy and running time of different methods on Pavia University dataset

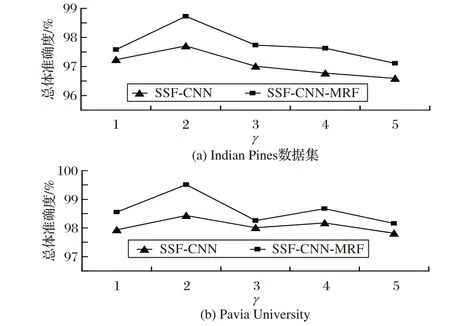
图8 选取不同γ值获得的分类结果Fig.8 Classification results with different γ values

3.5 与经典基于深度学习的高光谱图像分类方法的对比

为了进一步评估本文提出的SSF-CNN-MRF 算法的性能，本文比较了三种基于深度学习的高光谱图像分类算法:2DCNN［37］、3D-CNN［12］和DC-CNN［13］。2D-CNN［37］方法是利用二维卷积提取高光谱图像的空间信息，不考虑图像的光谱信息；3D-CNN［12］方法是在2D-CNN 的基础上实现的，可以提取高光谱的空间信息和光谱信息；DC-CNN［13］是利用一维卷积神经网络提取光谱特征，并利用二维卷积神经网络提取与空间相关的分层特征。对比方法都是目前在高光谱分类领域比较常用的效果较好的方法。通过对比实验，可以充分说明本文改进的高光谱图像半监督分类方法使分类精度进一步得到了提高。实验选择相同比例的训练样本，选择方法和前面的实验相同。

几种深度学习方法在两个数据集上获得的分类如图9 所示。从图9 可以看出:与其他方法相比，本文方法的视觉分类效果是最好的。如图9（a）所示，对于Indian Pines 数据集，其他算法将Corn-notill 类误分为Soybean-mintill 类，而本文SSDCNN-MRF 算法的这种误分明显得到了抑制；如图9（b）所示，在Pavia University 数据集上因为各种方法得到的分类精度都比较高，从视觉上观察本文方法的优势并不明显。因此后续对实验结果进一步进行了数值分析。

Indian Pine 数据集的定量实验结果如表3 所示。可以看出:与其他方法相比，本文SSF-CNN-MRF 算法得到了最佳的分类结果。表3 中的定量分析再一次验证了从视觉效果上得出的结论。在Indian Pines 数据集上，本文提出的SSF-CNNMRF 算法在6 个类别中有5 个类别都更接近真实标签的精度。和前一个实验情况类似，由于高光谱波段之间存在的信息冗余性，可能无法有效提取纯净且高质量的光谱和空间信息，无法保证每一种地物的分类效果都最好，但是与2DCNN［37］、3D-CNN［12］和DC-CNN［13］相比，该算法的OA 分别增加了2.22个百分点、0.92个百分点和0.34个百分点。

对于Pavia University 数据集，在表4中给出了具体对比结果。与其他深度学习方法相比，本文方法得到的OA、AA 和Kappa 均取得了最好的结果，这也说明本文方法整体的分类效果是最佳的。

表3 Indian Pines数据集上不同深度学习分类方法的分类精度和运行时间对比Tab. 3 Comparison of classification accuracy and running time between different deep learning classification methods on Indian Pines dataset

表4 Pavia University数据集上在不同深度学习分类方法的分类精度和运行时间对比Tab. 4 Comparison of classification accuracy and running time between different deep learning classification methods on Pavia University dataset

图9 不同深度学习分类方法的分类结果Fig. 9 Classification results obtained by different deep learning classification methods

从表1～4 中的实验运行时间可看出，本文方法比其他方法时间复杂度更高，这是由于本文算法不仅利用了标记样本，而且还充分考虑到高光谱图像中未标记的样本，所以不可避免地牺牲了时间性能。

4 结语

本文提出了一种基于卷积神经网络（CNN）和稀疏子空间聚类（SSC）的半监督深度学习框架，用于高光谱图像分类。该框架首先利用稀疏子空间聚类生成全部数据的伪标签，然后在一个卷积神经网络（CNN1）上进行预训练，并利用标记的训练样本对另一个卷积神经网络（CNN2）进行微调，进一步利用整个数据集提供的综合结构特征。此外，在预训练阶段，通过引入新的目标函数，解决了因为数据分布不平衡带来的样本分类难度差异和难以训练的问题。最后，马尔可夫随机场（MRF）作为图像后处理，鼓励邻近像素具有相同的标签，整个算法框架充分结合了光谱信息和空间信息，更有利于高光谱分类。实验结果表明，本文方法在两个高光谱图像数据集上分类性能优于其他深度学习方法。针对训练样本不足的情况，所采用的这种半监督深度学习框架在实际遥感应用中非常有意义。