穿越古长城的隧道开挖爆破振动参数预测模型

江东平，李龙福，朱 磊，李 明

(马鞍山矿山研究院爆破工程有限责任公司，安徽 马鞍山 243000)

岩体爆破产生的地震效应可引起附近建(构)筑物发生不同程度的破坏，对其安全稳定性有着极大的影响[1]，例如建(构)筑物出现不同程度的裂缝、结构失稳，甚至倒塌。

近年来由于爆破技术的发展及广泛应用，爆破地震效应问题日益突出，引起的民事纠纷事件也在不断增多，影响社会稳定。因此，加强爆破技术研究，特别是对爆破振动相关特征参数的分析，做出对建(构)筑物破坏的判别及预测，是当今工程爆破界必须认真研究和亟待解决的关键问题[2-4]。

支持向量机(SVM)是一种基于前苏联Vapnik教授[5]创建的统计学习理论而产生的一种新型学习机，是结构风险最小化原理的近似表达，加上其特有的模式分类泛化性能，与传统统计学相比，在解决小样本、非线性及高维模式识别问题中具有出色的学习能力[6-8]。因此，在穿越古长城的隧道爆破开挖过程中，基于Matlab平台构建SVM算法的爆破振动预测模型，利用该模型对爆破振动参数进行预测，以期指导爆破开挖作业。

1 支持向量机的基本原理

支持向量机的基本原理是通过建立合适的内积函数，采用非线性转换的方式，将输入空间转换到另一个更高维次的空间，然后在这个新的高维空间中寻求最优线性分类面，再求出分类函数，该函数在形式上与神经网络相似，其输出是若干中间层节点的线性组合，而每个中间层节点对应于输入样本与一个支持向量的内积[3]。

根据支持向量机的这一基本原理，将其应用到函数拟合中，即考虑用F(x)=w·x+b拟合数据{xi,yi}，i=1,…，n,xi∈Rd,yi∈R的问题。并假设所有的训练数据可用线性函数无误差地以精度ε拟合，即：

yi-ε≤w·xi+b≤yi+εi=1,…，n

(1)

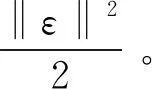
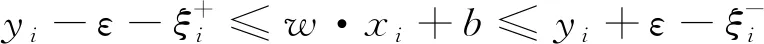
(2)

目标函数变为

(3)

利用优化方法可得上述问题的对偶问题，即

(4)

(5)

则回归函数为

(6)

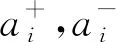
(7)

得到非线性回归函数：

(8)

利用该原理对训练数据进行拟合，在此过程中，并不需要具体的回归函数显示表达式，只要选取恰当的核函数，然后确定误差惩罚参数C、核参数σ及精度ε，即建立了在特定条件下的预测模型。

2 爆破振动参数预测模型的应用

2.1 工程概况

山西省某高速公路隧道位于晋蒙两省交界，且穿越古长城，地形平坦，两侧为黄土缓坡，植被稀疏，其中穿越的古长城为明朝在北部地区修筑的军事防御工程，距今已有600多年的历史。由于长期的风雨侵蚀、风沙淤漫和人为破坏，大部分只剩土垄，故对古长城的保护急为迫切。

隧道断面为圆弧拱，净宽12.2 m，净高8.1 m。隧道采用台阶法施工，上台阶高度6.1 m。区域岩性为强-中风化灰岩、石灰岩，岩体完整性较差，可采用钻爆法开挖。爆破任务重而频繁，在爆破地震波频繁而又连续的压、扭组合作用下，古长城极易形成裂缝。因此，在古长城基础拐角处布置测点，以研究爆破施工作业在该处的振动响应。

2.2 爆破振动参数的影响因素

根据李洪涛、许红涛等[9-10]的研究，影响爆破振动的主要因素有单段最大药量、高差、爆源距，次要因素有爆破分段数、总装药量、地质地形条件等。为了提高预测模型的训练速度，忽略爆破过程中对地震波特征参数影响较小的因素。由于隧道爆破开挖过程中使用的乳化炸药、延时雷管、装药结构及起爆方式相同，因此不考虑炸药、雷管类型和起爆方式对地震波特征参量的影响；同时因为采用固定监测点，爆破开挖所处区段的工程地质条件相似，故也忽略高差和工程地质条件的影响。最终选择孔径、孔深、孔距、排距、单段最大药量、总装药量和爆源距作为模型的输入参数。分别对水平径向(CH1)、水平切向(CH2)、垂直方向(CH3)进行爆破振动参数的预测。

2.3 模型学习、测试样本的选择

用于支持向量机学习训练的数据是在隧道正常开挖爆破时采集到的，分别为掌子面开挖爆破(上台阶、下台阶)和仰拱爆破开挖，3次爆破为一循环。一般情况下，上台阶爆破时单段最大药量与总装药量均大于其他工序的爆破，因此，只监测上台阶爆破时的振动数据。采用2#岩石乳化炸药，药卷直径32 mm，炮孔直径40 mm。共采集30 组爆破监测数据，取前20 组数据作为训练样本，后10 组数据作为测试样本。初始监测时固定监测点与台阶面的距离为144 m，爆破循环进尺1.7～2.1 m。设计掏槽孔单孔装药量1.6 kg，辅助孔单孔装药量1.4 kg，周边孔单孔装药量0.4 kg，底板孔单孔装药量1.4 kg，实际单孔装药量根据围岩地质情况适当调整，单段最大起爆药量为21.4～23.8 kg (7段)。炮孔布置与起爆顺序如图1所示，30组爆破参数中，孔径均为40 mm,孔深均为2.3 m,孔、排距均为0.8 m。其余爆破参数如表1所示。

注：圆圈表示炮孔；雷管延时均为毫秒段别
图1 炮孔布置与起爆顺序
Fig.1 Layout of blasthole and initiation sequence

表1 爆破参数

Table 1 Blasting parameters

编号单段最大药量q/kg总装药量Q/kg爆源距离R/m122.497.6144.0221.8100.0146.0322.2100.0148.1422.496.2150.1523.897.6152.0621.696.2154.0722.496.8155.8822.497.6157.9922.8100.0159.61023.096.4161.61122.295.8163.41222.497.6165.41321.495.8167.31422.4100.0169.21522.898.4171.01622.899.6172.81723.096.8174.71822.2100.0176.41922.496.4178.32021.495.8180.22122.497.6181.92222.895.8184.02322.896.4185.92422.4100.0187.72521.896.4189.52622.295.8191.52722.497.6193.42823.895.8195.22921.6100.0197.23022.499.2199.1

2.4 模型参数设置

根据杨成祥等[11]的研究结果可知，如果处理的计算模型比较复杂且对计算结果精度要求较高时，可以选择Gauss径向基核函数作为支持向量回归的核函数。通过调整参数法选取C、ε和核函数σ。根据训练结果，σ、C及ε的取值如表2所示，且在这3 个参数的取值结果下，模型的学习推广能力最佳。

表2 模型相关参数训练结果

2.5 对比分析

利用训练好的模型对后10 组爆破数据进行预测(3 个测试方向的最大值)，以检验模型的精确性，并与实测结果进行对比(见表3～表4)。

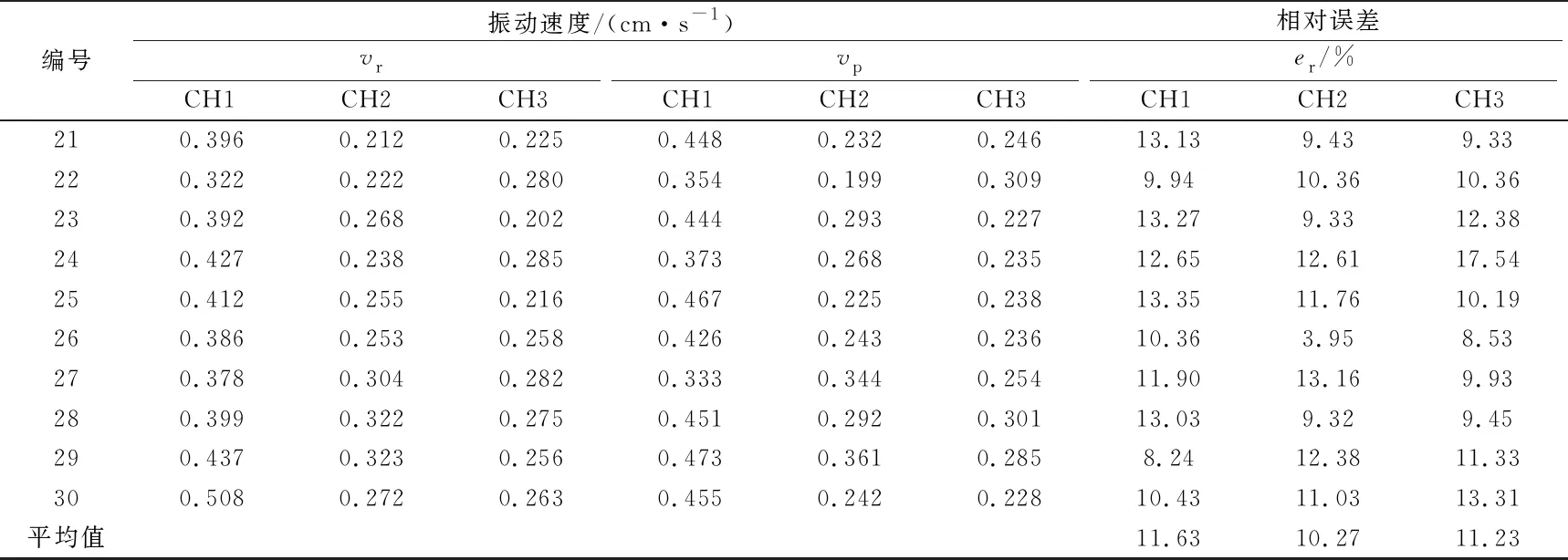
表3 实测振动速度与预测振动速度对比

注:vr、vp分别为实测振动速度与预测振动速度。

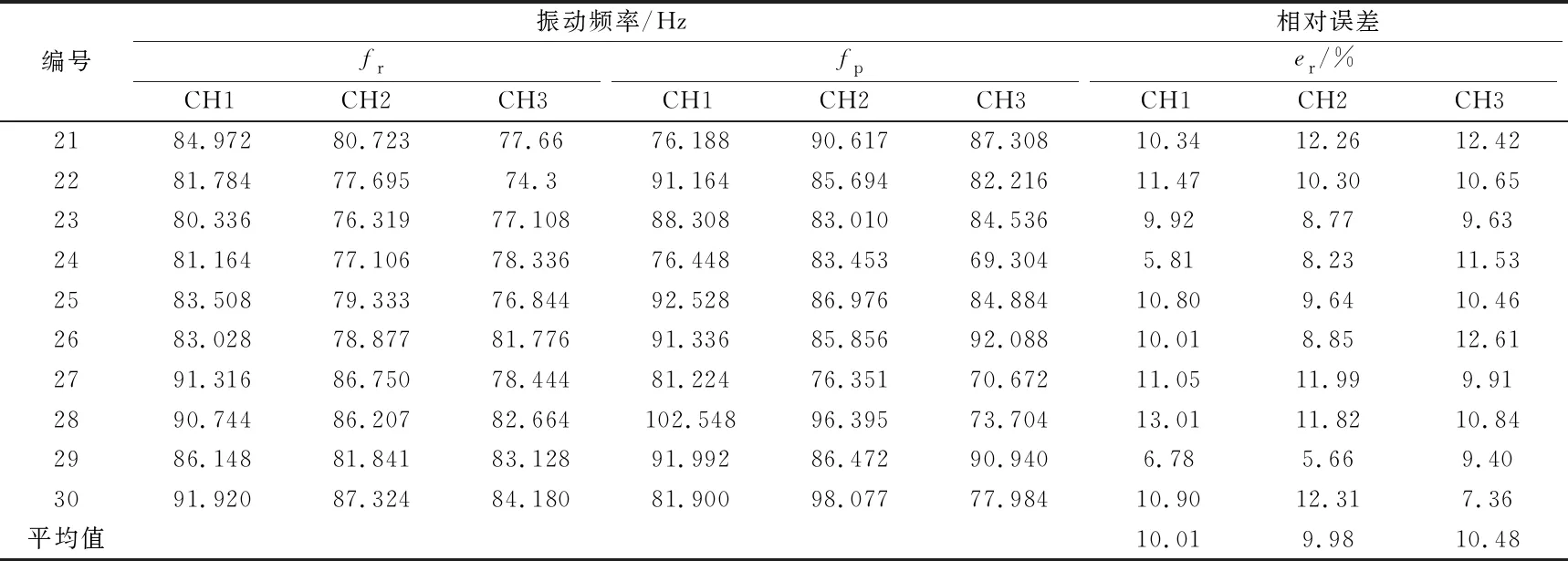
表4 实测振动频率与预测振动频率对比

注：fr、fp分别为实测振动频率与预测振动频率。

由表3可知，在爆破峰值振动速度预测中，支持向量机预测的水平径向、水平切向和垂直方向的相对误差平均值为11.63%，10.27%，11.23%；由表4可知，在爆破振动频率预测中，支持向量机预测的水平径向、水平切向和垂直方向的相对误差平均值为10.01%，9.98%，10.48%。

根据误差分析结果可知，支持向量机预测模型在爆破振动速度和振动频率的预测试验中具有较高的精度，平均误差分别为11.04%、10.16%。

3 结论

1)在爆破施工作业中，影响爆破振动的因素有很多，而且比较复杂，因此，选取多个主要的影响因素作为输入参数，建立了基于Matlab平台的支持向量机预测模型。利用监测的穿越古长城段施工爆破振动数据对模型进行检验。由监测数据的误差分析结果可知，支持向量机预测模型在爆破振动速度和振动频率的预测试验中具有较高的精度，平均误差分别为11.04%、10.16%。

2)在后续的爆破作业中，可利用该模型对爆破振动峰值速度及频率进行预测，根据预测结果结合《爆破安全规程》(GB 6722-2014)中对爆破振动安全的控制标准[12]，在保证古长城安全的前提下优化爆破参数和起爆网路，减少一次单段最大起爆药量，对爆破振动有害效应进行有效控制，可为穿越古长城的爆破施工起到良好的指导作用。