爆破地震波穿越不同介质结构面的衰减效应

董斌斌，程新锋，闫 雷，易文华，刘 伟，杨 砚，刘连生,2

(1. 江西理工大学资源与环境工程学院，江西 赣州 341000；2.江西省矿业工程重点实验室，江西 赣州 3410003；3.江西应用技术职业学院，江西 赣州 341000)

爆破地震波在不同充填介质中传播的衰减效应一直是工程爆破领域研究的热点问题[1-7]。众多学者围绕爆破地震波穿越结构面做了大量的研究。Zhao J 等[8]采用非线性模型—双曲弹性模型分析了节理数目不同对节理透、反射系数的影响；俞缙等[9-11]采用双重非线性法研究了应力波入射单个节理和多个节理的传播特征；Hao H 等[12]对应力波垂直入射节理面与平行入射节理面进行了探讨，发现两种不同的入射方式对应力波衰减快慢有显著区别；Li J C 等[13-14]提出了“虚拟波源(VWS)”的概念，运用粘弹性模型与非连续位移法分析了结构面厚度、入射角等因素对应力波的影响；范留明等[15]提出薄弹性夹层模型，发现入射角、波阻抗及厚度是影响应力波传播的主要因素，该模型在夹层透射解析方面分析较完善，夹层反射情况分析未作深入讨论；钱七虎等[16]对应力波在裂隙中的传播特性展开了研究，发现裂隙的完整性、泊松比和入射角对应力波衰减均有影响；孙金山等[17]对比了爆破地震波在顺层和反倾夹层中的传播差异；余永强等[18]对爆破地震波在断裂地层高应力作用下的振动特性展开了研究；张奇[19]对应力波从垂直方向穿越节理面展开了研究，结果表明，充填介质的纵波波速与应力波衰减显著相关，而应力波从其他方向穿越节理面时未探讨；刘希灵等[20]对弹性波在不同种类的岩石中传播进行了探讨，结果表明，岩石颗粒之间紧密度越高，弹性波衰减越慢，而弹性波在气态、液态介质条件中传播未作描述；刘婷婷等[21]提出三单元模型对充填结构面进行描述，从已有的理论对比分析了充填厚度、刚度以及充填介质波速与应力波传播的关系，尚未结合实际工程分析。上述研究普遍集中在结构面数目、入射角、厚度、刚度等方面对爆破地震波的影响，在理论研究上对结构面进行了理想化、简单化的假设，与实际工程依然有差距。

笔者基于混凝土边坡相似模型，结合试验采集的爆破振动数据，探讨爆破地震波穿越不同充填介质结构面的振动传播规律，为降低爆破振动效应提供相关依据。

1 爆破振动试验

爆破振动试验在混凝土边坡相似模型中进行，对比永平铜矿露天边坡岩体力学参数[22]，确定以水、425#硅酸盐水泥和筛选后的细沙按0.44∶1∶1.5的调配比例进行浇筑[23]，混凝土边坡相似模型力学参数如表1所示。设计的模型长2 700 mm，宽2 700 mm，高1 100 mm，一共有7层，包含6个台阶面，分别设置为0～6号测点，其中以0号测点为基准面，定义0号测点高程为0 mm，每个台阶的高度是120 mm，每个测点均设有预制螺杆，用于安装拾振器，边坡台阶坡面角均为67°，最终边坡角42°。模型的中心采用直径为8 mm的钢筋预制了25个炮孔，孔距、排距125 mm，孔深135 mm。模型分成8个区域，其中一个没有预制结构面定义为均质区域，其余7个区域的3号台阶分别预制倾角为15°、25°、35°、45°、55°、65°和75°的结构面，结构面长180 mm、宽450 mm、厚5 mm，模型浇筑成型后用泥、细沙、水和空气对结构面进行充填，充填介质物理参数如表2所示，混凝土边坡相似模型的尺寸大小和测点分布如图1所示。

表1 混凝土边坡相似模型力学参数

表2 不同充填介质物理参数

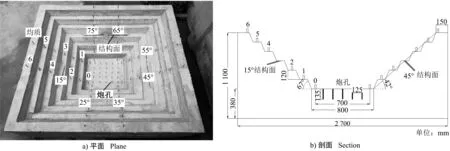
注：0～6为测点编号
图1 模型尺寸及测点布置
Fig.1 Model size and points layout

2 试验结果及分析

2.1 不同充填介质的振动速度分析

爆破振动试验中以起爆电子雷管的方式模拟炸药爆炸的过程，通过BlastmateⅢ型爆破测振仪采集爆破振动信号，该仪器的拾振器能够采集切向、垂向和径向的不同振动信号，不同振动方向的区分如图2所示。爆破振动测振仪配有相应的Blastware数据导出软件，在爆破测振完成后将数据线一端连接爆破振动测振仪，另一端连接电脑，操控Blastware软件即可将仪器监测的数据导入电脑，作为后期爆破振动信号处理分析的原始数据。试验按照充填介质的不同，分为4组试验。在每组工况下，分别将介质充填到不同倾角的结构面进行试验，故每组工况共做8次试验。每次试验时以模型的中心炮孔作为第1个炮孔，依次布置其他相邻2个炮孔(3个炮孔的连线指向爆破结构面)，3个炮孔同时起爆。每做完一组试验对结构面内的介质进行清理，然后重新充填另一种介质进行下一组试验，由于试验时使用电子雷管，药量小，各个炮孔可以循环使用。3号台阶是纵向空的不同倾角的结构面，结构面内依次充填泥、细沙、水和空气，为了探究爆破地震波穿越不同介质结构面的振动传播规律，对4号测点切向、垂向和径向的爆破振动信号进行采集，原始信号经过EEMD消噪后[24]的质点振动速度时程如图3所示，不同充填介质的峰值振动速度如图4所示。

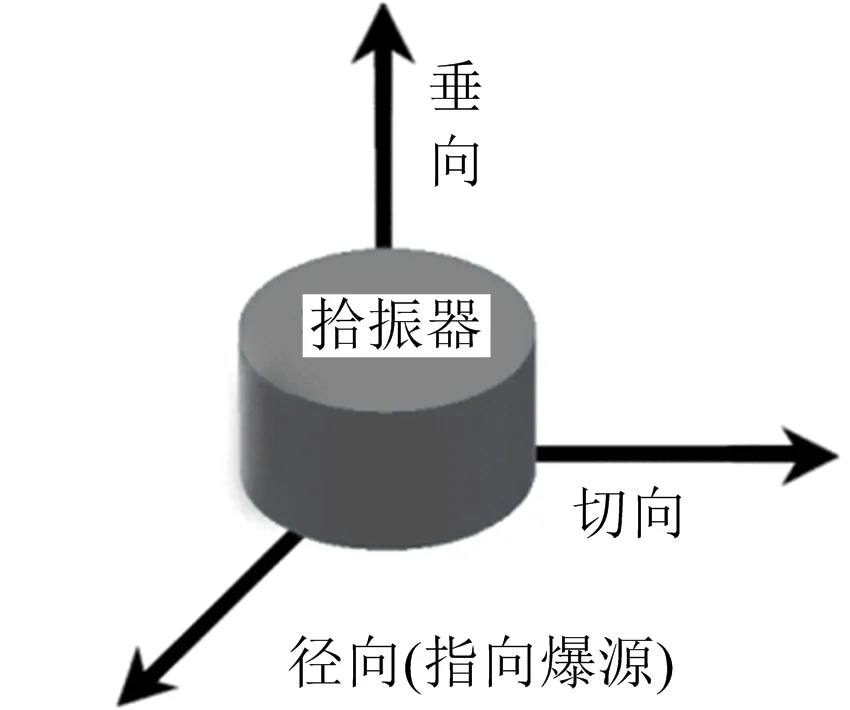
图2 不同振动方向
Fig.2 Different vibration directions

图3 质点峰值振动速度时程
Fig.3 Time history of particle vibration velocity

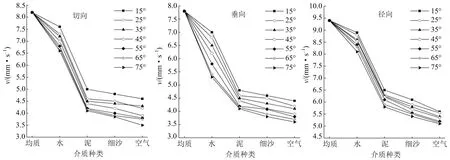
图4 不同充填介质的峰值振动速度
Fig.4 Peak vibration velocity of different filling media

结合图3和图4的峰值振动速度来看，无结构面的均质区域的峰值振动速度最大，其他不同充填介质的峰值振动速度要小于均质区域的峰值振动速度，由此可知爆破地震波穿越结构面后振动速度下降；对比不同充填介质的峰值振动速度，发现充填介质为水时峰值振动速度最大，泥、细沙次之，空气最小。一方面结构面内不同充填介质的波阻抗存在差异，均质区域是无结构面的均质台阶面，其波阻抗等于整个混凝土边坡相似模型的波阻抗。由表2可知，均质区域的波阻抗最大，泥的波阻抗大于水的波阻抗，水的波阻抗大于细沙的波阻抗，空气的波阻抗最小。当爆破地震波穿越同一个结构面时，结构面内充填介质的波阻抗越小，爆破地震波衰减越快，因此充填介质为泥的峰值振动速度大于充填介质为细沙的峰值振动速度，充填介质为细沙的峰值振动速度大于充填介质为空气的峰值振动速度；另一方面爆破地震波在气体、液体、固体介质中传播时也有所区别，当充填介质为空气时，结构面连续性最差，造成爆破地震波被阻隔无法穿越结构面，透射能量大幅度减小，因而峰值振动速度衰减最快。当充填介质为固体时，从微观结构分析，爆破地震波穿越结构面时，本质上是岩体内部一个个能量微单元由近到远振动传递的过程。固体微颗粒之间在自然状态下存在细微的空隙，当爆破地震波穿越结构面时，部分能量压缩固体颗粒之间的空隙，持续压缩空隙做功的过程消耗爆破地震波能量，其振动强度也相应减小。水由微压缩的流体质点构成，流体质点之间紧密相连，在空间上连续均匀分布，其空隙远远小于固体颗粒之间的空隙[25]，当爆破地震波穿越结构面时，能量微单元能在水介质中稳定传递，爆破地震波的透射性能大幅度提升，因此在不同充填介质的情况下，水的峰值振动速度最大。

2.2 不同倾角的振动速度分析

为了进一步探究爆破地震波穿越不同倾角结构面的峰值振动速度衰减趋势，在相同充填介质条件下，随着结构面倾角增大，各传播方向上的峰值振动速度均减小(见图5)。爆破地震波穿越结构面时会发生透射与反射现象，甚至有绕射现象，爆破地震波的透射能量随着结构面倾角增大而减小[26]，因此峰值振动速度也相应减小。随着结构面倾角增大，充填介质不同，不同传播方向上的峰值振动速度衰减程度也不同，表明爆破地震波速度衰减趋势是在岩体波阻特性、结构面内充填介质特征以及爆破地震波的透、反射现象等众多复杂因素影响下的综合体现。

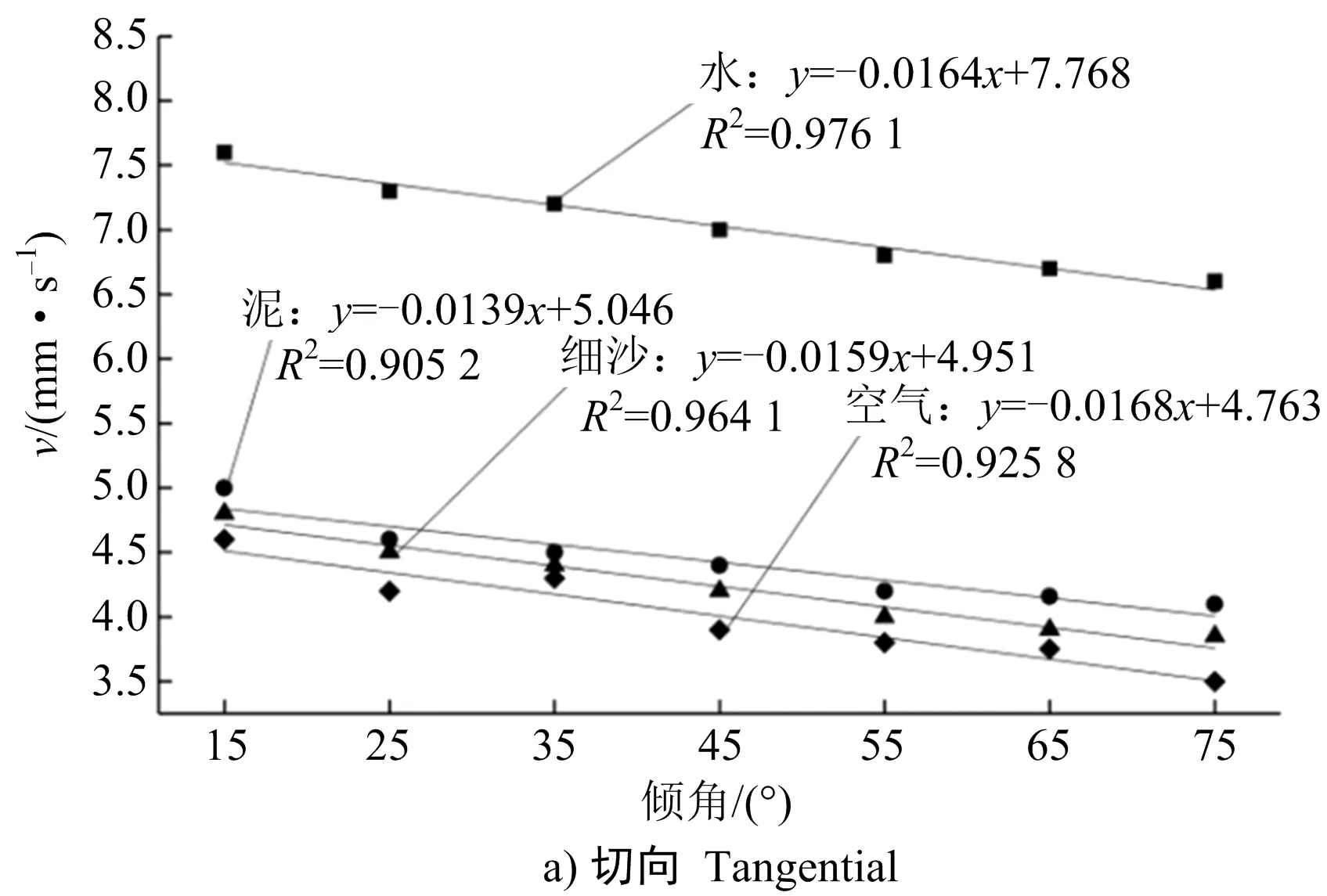
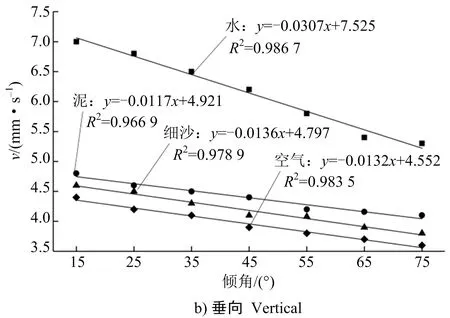
图5 不同倾角结构面的峰值振动速度拟合
Fig.5 Fitting of peak vibration velocity of different inclination structure surfaces

2.3 振动信号能量与频带分析

HHT(Hilbert-Huang Transform)是一种目前广泛运用于爆破振动信号处理的技术，与小波和傅里叶传统的分析技术相比，在处理信号的局部性和非平稳性等方面具有更大的优势，主要由经验模态分解(empirical mode decomposition，EMD)与Hilbert变换构成，Hilbert谱表达式为[27]

(1)

式中：Re表示取实部；αi，wi均为常数。

边际能量谱则是Hilbert谱进一步对时间(t)积分：

(2)

则频率i的能量占总能量的百分比为

(3)

边际能量谱能够反映爆破振动过程中能量与频率之间的分布特性，为了研究爆破地震波穿越不同充填介质结构面的能量和频率之间的规律，对4号测点均质区域和结构面区域的边际能量谱进行了分析，相应的边际能量谱如图6所示。

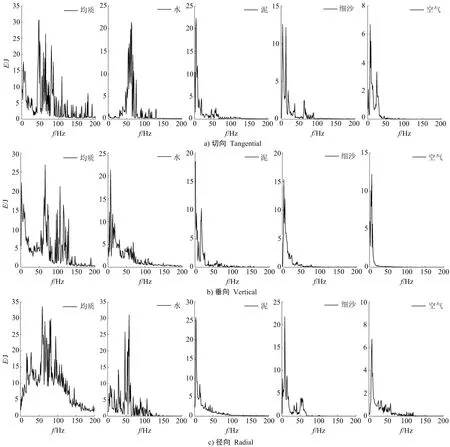
图6 不同充填介质的边际能量谱
Fig.6 Marginal energy spectrum for different filling media

结合图6分析，均质区域切向，垂向和径向上的峰值能量分别为30.76、26.88、33.65 J。当充填介质为水时，峰值能量分别为21.41、21.26、31.04 J；当充填介质为泥时，峰值能量分别为22.27、18.54、26.85 J；当充填介质为细沙时，峰值能量分别为12.58、15.36、21.75 J；当充填介质为空气时，峰值能量分别为6.67、12.23、6.75 J。由此可知，与有充填介质的结构面相比，均质区域的峰值能量明显更大，表明当爆破地震波穿越结构面后能量衰减，峰值能量相应减小；由于结构面内充填介质波阻抗不同，峰值能量衰减快慢也不同，可以发现充填介质的波阻抗差异是影响爆破地震波能量衰减的重要因素，结构面内充填介质的波阻抗减小，峰值能量也相应减小；值得注意的是，水的波阻抗小于泥的波阻抗，充填介质为水的峰值能量却高于充填介质为泥的峰值能量，由此可见爆破地震波在水介质中传播时，不仅水的波阻抗会影响地震波的衰减，而且水的连续性也会影响地震波的衰减，水能连续充满其所占据的结构面空间，使结构面连续性比泥、细沙充填的结构面都要密实，同时水的压缩性小，质点间紧密相连，分布均匀，爆破地震波在其传递过程中能量消耗相对也就越小。

进一步对比了不同充填介质在不同频带间的能量百分比(见图7)，可以发现爆破地震波能量集中在0～200 Hz，在此频率范围内分为若干个频带，主频带则是在各频带中能量占比最大的频带。在均质区域的能量分布广泛，在各频带间均有分布，切向、垂向和径向上的主频带均集中在60～80 Hz，能量百分比分别为23.67%、22.22%和19.8%。由于结构面的影响，不同充填介质的能量在低频带更集中，主频带多集中在0～20 Hz，主频带有往低频集中的趋势，由此可见，结构面存在“低通”特性[22,28-31]，即结构面对爆破地震波具有高频滤波作用，低频波能够更容易透射结构面。当充填介质为泥时，在0～100 Hz的能量百分比在93.34%～97.22%，充填介质为细沙时，在0～100 Hz的能量百分比在96.25%～99.62%，可知充填介质为细沙时，能量在0～100 Hz的频带分布更多，当充填介质为空气时，能量多分布在0～60 Hz，百分比在88.6%～97.68%之间，由此可以发现，结构面内充填介质的波阻抗越小，高频波衰减越快。当充填介质为水时，分布在0～160 Hz的能量占总能量的比例为96.68%～99.73%，其中主频带在各传播方向上分布不一，切向主频带为60～80 Hz，能量百分比为43.24%，垂向主频带为0～20 Hz，能量百分比为37.61%，径向主频带则分布在40～60 Hz之间，能量占比为43.71%。由此可知，当充填介质为水时，能量主要分布在0～160 Hz，与其他充填介质比较而言，频带分布更广；水在结构面内是无固定形状的液态，当爆破地震波传递至结构面时，液体中的粒子因振动传播无法保持原来的位置而产生移动，但粒子间存在相互作用力，使彼此不分散远离，形成了连续流动的状态，连续流动的液体在各传播方向上过滤高频波的特性不一致，因而爆破地震波的主频带在各传播方向上分布不一。

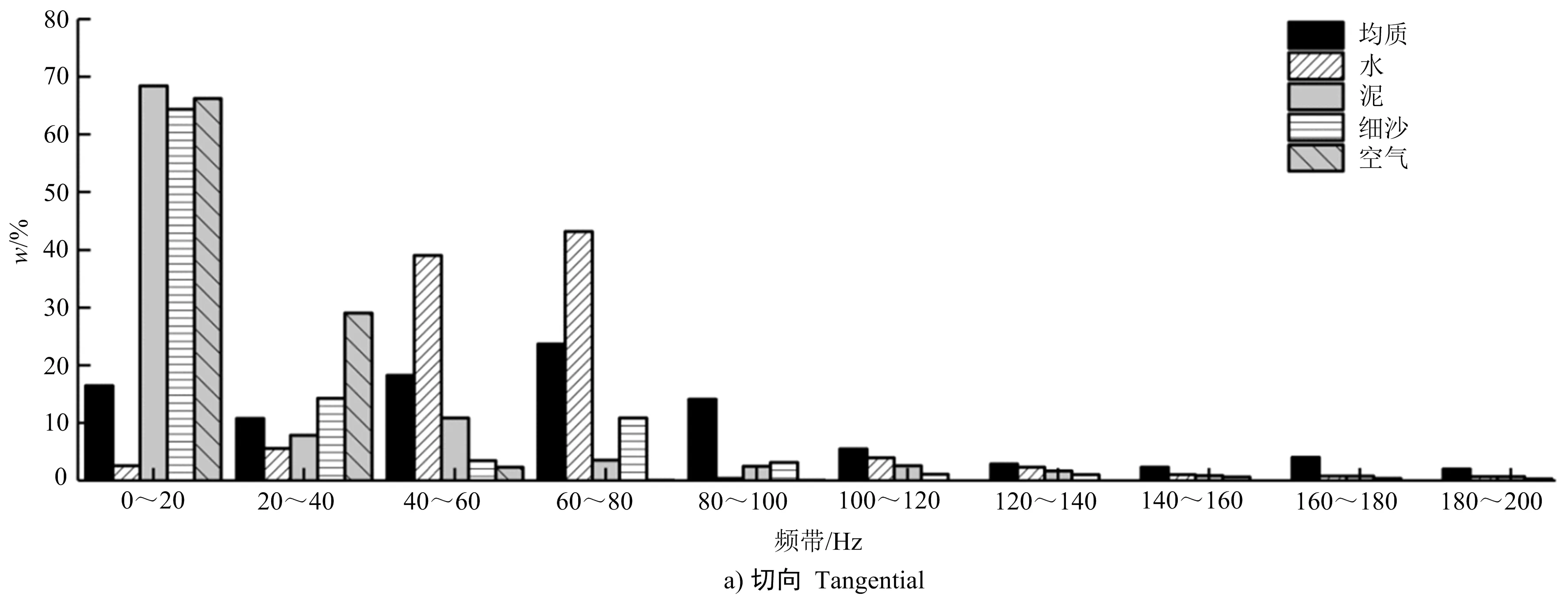
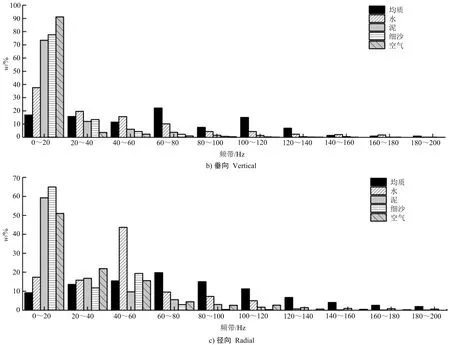
图7 不同充填介质的各频带能量百分比
Fig.7 Percentage of energy per band of different filling media

3 结论

1)通过分析对比均质区域(无结构面)与结构面充填水、泥、细沙和空气的不同介质，得到各传播方向上的峰值振动速度由大到小排序依次为均质、水、泥、细沙、空气。这是由于爆破地震波在气体、液体，固体介质中的传播特性不同和结构面内充填介质波阻抗不同的响应结果。

2)在相同充填介质条件下，随着结构面倾角增大，各传播方向上的峰值振动速度均减小；充填介质不同，不同传播方向上的峰值振动速度衰减程度也不同，表明爆破地震波速度衰减趋势是在岩体波阻特性、结构面内充填介质特征以及爆破地震波的透、反射现象等众多复杂因素影响下的综合体现。

3)爆破地震波在穿越不同充填介质结构面后，充填介质的波阻抗越小，峰值能量越小，高频滤波作用越强，表现出爆破地震波在频带间能量分布变窄，主频带有往低频带(0～20 Hz)集中的趋势；值得注意的是，当水作为充填介质时，不仅水的波阻抗会影响地震波的衰减，而且水的微压缩连续性也会影响地震波的衰减，与其他充填介质比较，水的连续性使峰值能量和峰值振动速度衰减更慢，能量在频带间分布更广，水的流动性则会造成爆破地震波的主频带在各传播方向上分布不一。