次分数布朗运动环境下最值期权定价
梁喜珠, 薛 红, 王 瑞
(西安工程大学 理学院,陕西 西安 710048)
期权定价一直是金融数学研究的热点问题之一。1973年Black和Scholes创立了第一个完整的期权定价模型[1],之后随着期权市场的迅速发展,期权定价理论的研究取得了突破性进展。最值期权作为一种新型期权,最初是由Stulz[2]研究的。文献[3-4]讨论了两种以上资产在几何Brown运动环境下的最值期权定价公式。研究表明,风险资产的价格不能被简单地看成服从几何Brown运动,于是引入了分数Brown运动。Hu和Øksendal[5]证明了分数Brown运动能够更合理地描述标的资产的价格。文献[6-7]利用保险精算方法给出了分数Brown运动环境下最值期权的定价公式;文献[8-9]分别利用拟鞅定价和拟条件数学期望理论,求得了多个标的资产在分数Brown运动环境下最大值期权的定价公式。
随着深入研究,人们开始使用修正的分数Brown运动,例如次分数Brown运动来描述标的资产的价格变化[10-11]。Tudor指出次分数Brown运动是较为一般的高斯过程[12],其性质类似于分数Brown运动,不同之处是其增量非平稳[13-14]。Yan[15]等给出了次分数Brown运动的随机积分,并指出金融资产的随机波动性可以用它来刻画。文献[16-17]分别利用偏微分方程和Wick-Ito积分研究了次分数Brown运动下带交易费用的备兑权证定价问题和支付红利的欧式看涨期权定价问题。本文在标的资产价格服从次分数Brown运动的环境下,运用保险精算的方法,推导最值期权的定价公式。
1 次分数布朗运动环境下金融市场模型
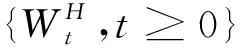
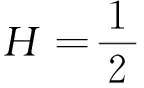
假设金融市场有n种风险资产,其价格Si(t)满足方程
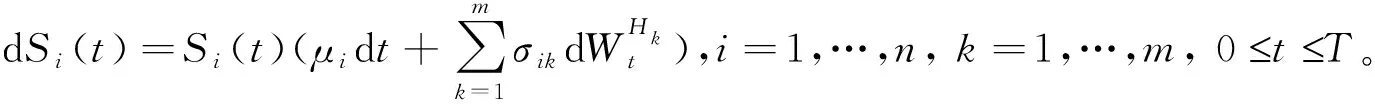
(1)
引理1[14]随机微分方程(1)的解为
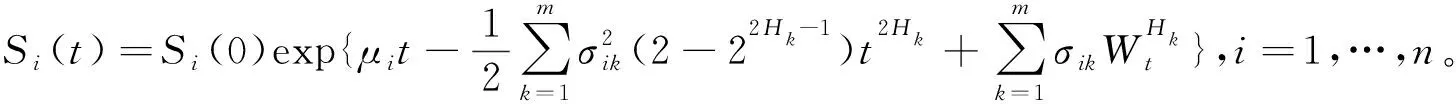
(2)
定义2[19]资产价格{Si(t),t≥0}在[t,T]上的期望回报率βi(u),u∈[t,T]定义为
引理2[20]资产价格{Si(t),t≥0}在[t,T]上的期望回报率βi(u),u∈[t,T]满足
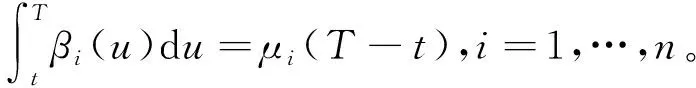
(3)
2 两种资产的最大值期权定价
定义3[2]到期日为T,执行价格为X,资产Si(T),Sj(T)的最大值欧式看涨、看跌期权在t时刻的保险精算价格定义为


其中无风险资产X以无风险利率r折现,资产价格Si(T),Sj(T)按其期望回报率βi(u),βj(u)折现。
定理1到期日为T,执行价格为X,资产价格Si(T),Sj(T)的最大值欧式看涨期权在t时刻的保险精算价格
cmax=Si(t)N(ci,di;ρi)+Sj(t)N(cj,-dj;-ρj)-Xe-r(T-t)[1-N(-bi,-bj;ρij)]。
(4)
其中
ci=bi+σi, di=aij+ρiσi,
cj=bj+σj, dj=aij+ρjσj,
证明令

于是

=E[e-μi(T-t)Si(T)I{-ηij ≜E1+E2-E3, 其中 E1=E[e-μi(T-t)Si(T)I{-ηij =Si(t)N(ci,di;ρi)。 同理E2=Sj(t)N(cj,-dj;-ρj),E3=Xe-r(T-t)[1-N(-bi,-bj;ρij)]。 因此cmax=Si(t)N(ci,di;ρi)+Sj(t)N(cj,-dj;-ρj)-Xe-r(T-t)[1-N(-bi,-bj;ρij)]。 定理2到期日为T,执行价格为X,资产价格Si(T),Sj(T)的最大值欧式看跌期权在t时刻的保险精算价格 pmax=Xe-r(T-t)N(-bi,-bj;ρij)-Si(t)N(-ci,di;-ρi)-Sj(t)N(-cj,-dj;ρj), (5) 其中N(x,y;ρ),bi,bj,ci,cj,di,dj,ρi,ρj,ρij见定理1。 证明类似于定理1的证明,有 =Xe-r(T-t)P{ηi<-bi,ηj<-bj}-E[e-μi(T-t)Si(T)I{-ηij =Xe-r(T-t)N(-bi,-bj;ρij)-Si(t)N(-ci,di;-ρi)-Sj(t)N(-cj,-dj;ρj)。 推论2关于资产Si(T),Sj(T)的最大值欧式看涨期权与看跌期权的平价关系 cmax-pmax=Si(t)N(di)+Sj(t)N(-dj)-Xe-r(T-t)。 证明由定理1与定理2以及正态分布性质可得。 当H1=H2=H3=H=0.3,0.5,0.7时,运用MATLAB软件计算两资产最大值看涨期权在0时刻的保险精算价格,如表1所示。 表1 不同H参数下最大值看涨期权价格 由此可看出,当H1=H2=H3=H取不同值时,两种资产的最大值期权价格有显著性差异;当H1=H2=H3=H=0.5时,即为几何Brown运动下最大值期权价格,而当H1=H2=H3=H≠0.5时,即为一般次分数Brown运动下最大值期权价格;从而可知,市场不同的分形结构对期权价格有显著性影响。 定理3到期日为T,执行价格为X,多种资产S1(T),S2(T),…,Sn(T)的最大值欧式看涨期权在t时刻的保险精算价格 (6) 其中 ci=bi+σi,i=1,…n,dij=aij+ρij,iσi,i,j=1,…n, 证明令 由于 X≜(η1,η2,…,ηn)~N(0,Σ), Xi≜(ηi,ηi1,…,ηi(i-1),ηi(i+1),…,ηn)~N(0,Σi),i=1,2,…,n, 其中0=(0,0,…,0)为n维零向量,协方差矩阵Σ,Σi为n×n阶正定对称矩阵。 因此 =E[e-μ1(T-t)S1(T)I{-η1j +E[e-μn(T-t)Sn(T)I{-ηnj -Xe-r(T-t)[1-N(-b1,-b2,…,-bn)] -Xe-r(T-t)[1-N(-b1,-b2,…,-bn;Σ)] =S1(t)N(c1,d12,d13,…,d1n;Σ1)+S2(t)N(c2,d21,d23,…,d2n;Σ2)+… +Sn(t)N(cn,dn1,dn2,…,dn(n-1);Σn)-Xe-r(T-t)[1-N(-b1,-b2,…,-bn;Σ)] -Xe-r(T-t)[1-N(-b1,-b2,…,-bn;Σ)]。 同理可讨论多种资产的最大值看跌期权以及多种资产的最小值看涨和看跌期权的保险精算价格。 本文在传统模型的基础上,利用保险精算方法,探讨了次分数布朗运动环境下两种资产的最大值期权定价公式,并对其进行了推广,得到了相同条件下多种资产的最大值定价公式.对于两种资产和多种资产在次分数跳-扩散过程下的最值期权定价,还有待于进一步讨论研究。
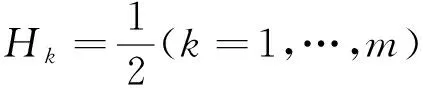
4 数值计算与分析

5 多种资产的最大值期权定价



6 结论

