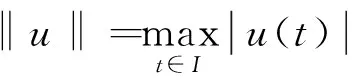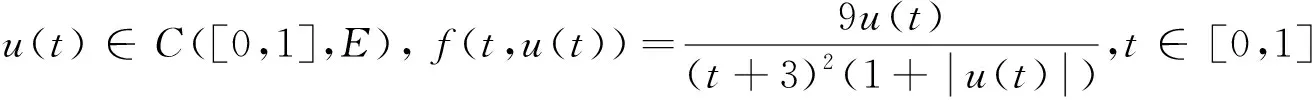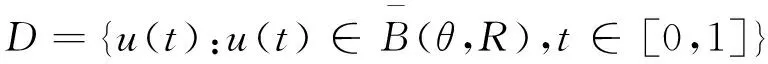分数阶微分方程初值问题mild解的存在性
柴建红, 周文学, 孙 芮, 周玉群
(兰州交通大学 数理学院,甘肃 兰州 730070)
引言
在电磁学,力学,医学,扩散,控制,信息处理等实际应用中,分数阶微分方程比整数阶微分方程更符合实际情况,因此这引起了许多学者的关注与研究。近些年,许多学者研究了分数阶发展方程mild解的存在性,唯一性。其中,发展方程是指含有未知函数关于时间变量t的导数或偏导数的微分方程的统称。在文献[1]中,El-Borai首次引入概率密度函数用于研究分数阶微分发展方程并得到了其古典解。周勇和王锦荣等也研究了阶数为0 (1) mild解的存在性及正mild解的存在性进行研究。其中Tq是指阶数为0 定义1[6]设q∈(n,n+1]且f:[0,∞)→R,f的一致分数阶导数可定义为 常用f(q)表示,其中[q]表示大于等于q的最小整数。 特别地,在本文中q∈(0,1),则 引理1[6]设q∈(0,1],函数f和g在t>0上q次可微,则 (1)Tq(af+bg)=aTq(f)+bTq(g),∀a,b∈R; (2)Tq(tp)=ptp-1,∀p∈R; (3)Tq(λ)=0,∀λ∈R; (4)Tq(fg)=fTq(g)+gTq(f); 引理2设f∈C(I,R),其中I=[0,a],对于下列分数阶发展方程初值问题 (2) 存在mild解 (3) 证明方程(2)由引理1中的性质(6)知等价于下列的微分方程 对上式两端同时积分,有 定义2[9]设E为实Banach空间,S是E中的有界集。令 引理3[9]非紧性测度α(·)具有如下性质: (1)α(S)=0⟺S为相对紧集; (2)S⊂T⟹α(S)α(T); (4)α(S∪T)max {α(S),α(T)}; (5)α(aS)=|a|α(S),其中aS={x:x=ay,y∈S}; (6)α(S+T)α(S)+α(T),其中S+T={x:x=y+z,y∈S,z∈T}; 引理4[9]设E为Banach空间,若B⊂C(I,E)有界且等度连续,则α(B(t))在I上连续,且 引理5[10]设E为Banach空间,若B={xn}⊂C(I,E)为可列集,存在g(t)∈L1(I),使得 ‖un(t)‖g(t),a.et∈I,n=1,2,… 则α(B(t))∈L1(I),且有 特别地,当B有界时,上式成立。 引理6[11]设D⊂E有界时,则存在D的可数子集D0⊂D,使得 α(D)2α(D0)。 定义3[12]设E1,E2为实Banach空间且D⊂E1,设A:D→E2连续有界,若对任何非相对紧的有界集S⊂D都满足 α(A(S))<α(S)。 则称A是D上的凝聚映射。 引理7[9](Sadovskii不动点)设E为Banach空间,D是E中的有界闭凸集(D不一定有内点)。若Q:D→D为凝聚映射,则Q在D中必有不动点。 定义4[13]设E为Banach空间,B(E)表示E中所有线性有界算子构成的Banach空间,若T(t):[0,+∞)→B(E)满足 (1)T(0)=I; (2)T(s+t)=T(s)T(t),∀t,s∈R+。 则称T(t)(t≥0)为E中的线性算子半群。 定义5[13]设T(t)(t≥0)为E中的线性算子半群。下列方式定义线性算子A 称为T(t)(t≥0)的无穷小生成元。 定义6[14]设T(t)(t≥0)为E中的线性算子半群,若对∀x∈E,有 则称T(t)(t≥0)为E中的强连续半群或C0-半群。 定义7[14]设T(t)(t≥0)为E中的C0-半群。若对∀x≥θ,有T(t)x≥θ,t≥0,则称T(t)(t≥0)为E中的正C0-半群。 引理8[14](指数有界性)设T(t)(t≥0)为E中的C0-半群,则存在常数M≥1,ω≥0使得 ‖T(t)‖Meωt,t≥0 特别地当ω=0时,T(t)(t≥0)为E中的一致有界C0-半群。 引理9[15](Gronwall引理)设b≥0,q>0,h(t),u(t)是区间[a,b]上局部可积的非负函数,若 u(t)h(t)+b(t-s)q-1u(s)ds, 则 u(t)tb 引理10[16]设1p∞,对于可测函数m:I→R,定义范数 为方便起见,本文总假设如下 (H1)函数f:I×E→E满足下列条件 (ⅰ)对∀t∈I,函数f(t,·):E→E是连续的; (ⅱ)对∀u(t)∈E,函数f(·,u(t)):[0,a]→E是Lebesgue可测的。 ‖f(t,x)‖m(t) (H3)存在常数L>0,使得对∀t∈I,D⊂E,有 α(f(t,D))Lα(D) (H4)对于任意的常数R>0,存在常数K>0,使得当θx1x2, ‖x1‖,‖x2‖R时,有 f(t,x2)-f(t,x1)≥K(x2-x1),t∈I (H5)对于任意的常数R>0,存在常数L>0,使得对任意的单调递增序列 有 α(f(t,D))Lα(D),∀t∈I 证明定义积分算子Q:C(I,E)→C(I,E)如下 (4) 则(Qu)(t)为连续算子,且初值问题(1)的mild解等价于积分方程(4)中Q的不动点,令 由引理11和条件(H2),对∀t∈I,有 由引理8知,有 (5) 第一步:映射Q:Ω→Ω。取∀u∈Ω,由(5)式,有 ‖(Qu)(t)‖ 所以Qu∈Ω,即Q:Ω→Ω。 第二步:Q(Ω)为C(I,E)中的等度连续函数。对∀u∈Ω,0t1t2a,由(4)式知,有 ‖(Qu)(t2)-(Qu)(t1)‖ =I1+I2+I3, 其中 因为T(t)在I=[0,a]上连续,所以T(t)在I=[0,a]上也是一致连续。对于I1,I2,当t2-t1→0时显然趋于0。对于I3由Lebesgue控制定理及以T(t)的一致连续知,当t2-t1→0时,I3也趋于0。 综上可得,当t2-t1→0时,‖(Qu)(t2)-(Qu)(t1)‖→0。故Q(Ω)为C(I,E)中的等度连续函数。 第三步:Q:Ω→Ω为凝聚映射 α(Q(B1)(t))=α(Q(un)(t)) 所以α(Q(B))又因为故Q:Ω→Ω是凝聚映射。 则由Sadovskii不动点定理可知,Q在Ω中有不动点且该不动点为方程(1)在I=[0,a]上的mild解。 证明由定理1知,方程(1)在区间I=[0,a]上至少存在一个mild解u∈C(I,E)。令h*>0,在区间[a,a+h*]上定义u(t)=v(t),通过这种方法可以将方程(1)的mild解u(t)向右延拓到更大的区间[0,a+h*],其中v(t)是下列分数阶发展方程初值问题 在[a,a+h*]上的解,其中h*与h,u(h)有关。接着依次重复此过程就可以得到极大区间[0,T),使得u∈C([0,T),E)为分数阶微分发展方程(1)的饱和mild解。 C(T)=sup { ‖f(t,u(t))‖:0tT+1,‖u(t)‖R(T)}。 对∀t1,t2∈(0,T]且令0 对于下列分数阶发展方程初值问题 C=sup {‖f(t,u(t))‖:0tT,‖u(t)‖M(R*+1)}。 ‖u(t)‖M(R*+1),u(tn+hn)=M(R*+1) 其中tn M(R*+1)=‖u(tn+hn)‖ →MR*(hn→0)。 定理2设E为有序Banach空间,其正元锥P为正规锥,A生成E中一致有界的等度连续的正C0-半群T(t)(t≥0)。设x0≥θ,f∈C(I×E,E)且f(t,θ)≥θ。若f满足条件(H1),(H4),(H5),则分数阶微分发展方程初值问题(1)存在正的mild解u(t)∈C(I,P)。 证明设R0为定理1证明中定义的常数,由(4)式知,Q:C(I,P)→C(I,E)是增算子。因为取∀u1,u2∈P且θu1u2,由(H4)及正C0-半群T(t)(t≥0)可知 ≥0。 取Ω1={u∈C(I,P):‖u‖R0},则Ω1为C(I,E)中的有界凸闭集,对∀u∈Ω1,由Q的序增性知,有 又由定理1的证明可知Q:Ω1→Ω1。取u0≡θ∈Ω1,作迭代序列{un},使得 un=Qun-1,n=1,2,… (6) 则有 θ=u0u1u2…un… (7) 下证{un}收敛,记B0={un:n=0,1,2,…},B1={un:n=1,2,3,…},根据(4)式,对于∀t∈I,由引理5和条件(H5)知,有 α(B1(t))=α((Qun-1)(t)) 证明类似推论1的证明。 令 取∀x∈H,有 则H⊂D。 =α(H)α(D)。 即存在L=1,使得α(f(t,D))α(D)成立。根据定理1知,此初值问题存在mild解u(t)∈C([0,1],E)。1 预备知识
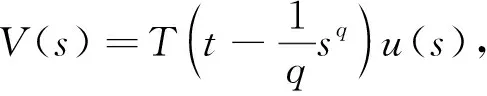



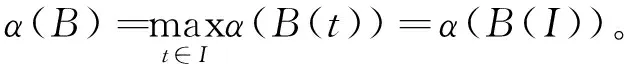

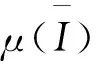


2 主要结果及证明
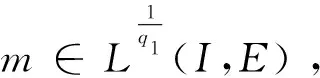





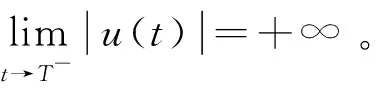
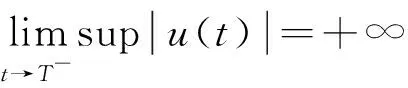
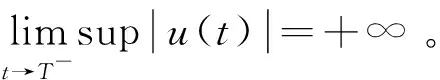
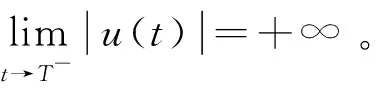

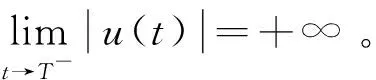

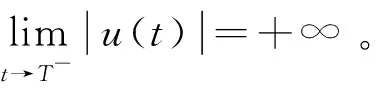
3 例题