倾斜磁场中各向异性抛物量子盘的光吸收特性

牛牧文， 李学超， 叶纯宝， 高 娟

(安徽理工大学 力学与光电物理学院，安徽 淮南 232001)

引言

半导体量子体系因其形式上的多样性以及光电性质的丰富性，在光电研究领域一直都具有重要意义并且受到广泛关注。块材料由于其宏观特性，非线性光学响应较差，而低维半导体材料可将电子限制在量子尺寸的半导体结构中，从而具有明显的量子效应，其光学性质表现出较强的非线性[1-3]。近年来，随着分子束外延生长及蚀刻、金属有机气相沉积[4，5]等纳米半导体结构制造技术的发展，人们已经能够制造出多种形式的受限量子体系，如量子阱、量子线以及量子点等[6]。这些体系中由于量子局域效应使其具有离散的能级以及特殊的光电特性[7，8]，在量子计算和光电器件制造等领域具有十分广泛的应用，例如量子加密和激光器等，其中后者在应用激光诱导击穿光谱仪进行元素检测方面具有重要作用，如合金中的杂质元素检测[9]。解文方等[10]研究了量子点的形状对光吸收系数的影响，他们发现量子点的形状对光吸收系数有着重大的影响。Ozturk等[11]研究了势垒宽度对三重GaAlAs/GaAs和GaInAs/GaAs量子阱的光吸收系数的影响，结果表明子带间的吸收光谱随势垒宽度的变化显现出蓝移或红移的特性。郭康贤等[12]研究了如何增强球形圆顶半导体纳米壳层的非线性光学效应，研究发现利用表面等离子共振效应可以极大的增强球形圆顶半导体纳米壳的非线性光吸收性质。由于能够影响纳米半导体结构非线性光学性质的因素众多(如量子点几何形状、极化子效应、杂化效应等)，我们研究了斜磁场中且受限势为抛物势的量子盘系统的光吸收性质。结果表明该系统的光吸收系数具有高度可调性。

1 理论模型

假设电子被束缚在量子盘中，在倾斜磁场作用的条件下，运用有效质量近似，量子盘中电子的哈密顿量可表示成如下形式[13]

(1)

其中，m*为电子的有效质量，P表示电子的动量，A为磁矢势，V(x,y)为受限势，具体形式如下

(2)

其中，ωx与ωy分别为沿x方向和y方向上受限势的频率。讨论电子在xy平面的运动，此时系统在倾斜磁场中的哈密顿量表示为

(3)

(4)

作以下变换

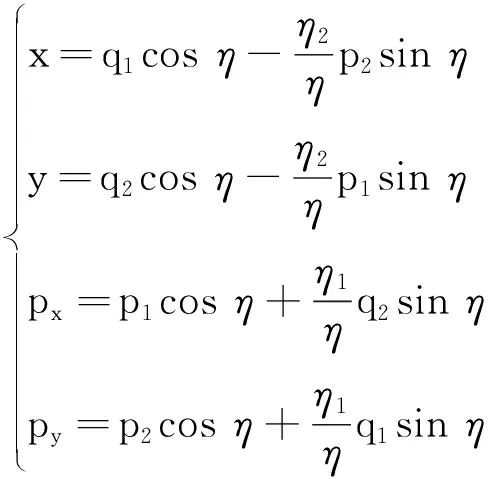
(5)

若η1η2=η2，则存在对易关系：[pi,qj]=-iћδij和[qi,qj]=0，同时将方程(5)代入到方程(3)中，当满足条件：

(6)

系统哈密顿量可对角化，此时新的哈密顿量可以表示为

(7)

其中，A、B、C和D分别为

(8)

在上述方程中，参数λ定义为

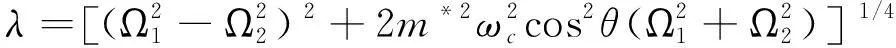
(9)

根据方程(7)，可以得到系统的能级为

(10)

其中，ω1=AB/m*及ω2=CD/m*。

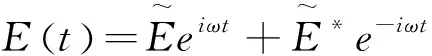
(11)

其中，H0表示无光场作用时的零级哈密顿量，Γij表示弛豫率，ρ(0)为未受扰动的密度矩阵算符。密度矩阵ρ可做如下迭代

使用环境会为产品设计提供许多好思路。在掌握环境条件特点的同时，要构思这样的环境条件适合什么样的结构、什么样的材料等等。很多设计方案就可从此中产生。环境的限制,必然又要求设计师要尽力地适应环境的特点,否则就使设计方案在特定环境条件下无法完成作业要求。例如，有些劳动项目在多雨的南方要求全天候作业，如果农具不具备防水能力，就会无法完成作业要求。另外，为了适合不同环境的作业要求，可以采用可调节设计，以增强产品的适应环境的能力。让产品适应其使用环境,实质上是要求设计师利用环境条件、克服环境限制,设计开发出适合环境要求的合理的可行方案[4]。

(12)

其中

(13)

在入射光场的作用下所引起的极化强度与极化率的关系如下

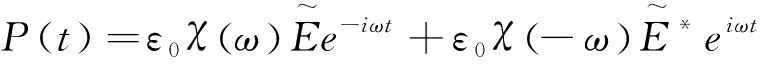
(14)

(15)

其中V和M分别表示相互作用体积和电偶极矩。

通过方程(11)—(15)我们可以推导得到一阶线性和三阶非线性极化率的表达式分别如下

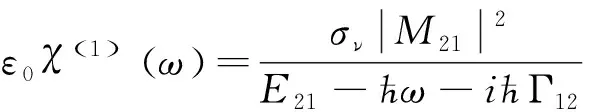
(16)

(17)

其中δν表示电子密度，Mij=|Ψi|M|Ψj|表示偶极跃迁矩阵元，Eij=Ei-Ej表示两种不同电子态的能量间隔。

吸收系数与极化率之间有以下关系[14]

(18)

利用密度矩阵理论以及迭代法，我们可以得出系统总的光吸收系数，表达式如下

α(ω,I)=α(1)(ω)+α(3)(ω,I)

(19)

其中

(20)

(21)

分别为一阶线性和三阶非线性的光吸收系数表达式。在以上表达式中，μ表示体系的磁导率，εR表示体系介电常数的实部，nr表示介质的折射率，I为入射光的光强，c为光速。

3 结果与讨论

在本部分，我们将以GaAs/AlGaAs量子盘为对象，计算其线性和非线性光吸收系数并且给出数值结果，然后就其结果进行讨论。计算过程中所使用的参数为：m*=0.067m0(m0为自由电子的质量)，nr=3.2，Τ12=0.2ps，Γ12=1/Τ12，B=10T，δν=5.0×1024m-3[15-16]。

如图1所示，我们在I=0.1MW/cm2,θ=60°,ωy=50.54ps-1的条件下，做出了当ωx分别取50.54ps-1、52.79ps-1、55.04ps-1时，总光吸收系数随光子能量ћω变化的关系图。从图中我们可以看出随着ωx值的增大，总的光吸收系数也随之增大。这是因为当x方向上受限势频率增大时，偶极跃迁矩阵元Mij也随之变大，由方程(21)和(22)可知，光吸收系数也增大。此外明显还有一个蓝移现象，即随着ωx的增加，共振峰的位置向能量高的区域移动。出现此种现象的原因是因为随着束缚势能ωx的增加，各能级间的间距增大，导致光吸收系数峰值向光子能量高的位置移动。

在图2中，我们保持I=0.1MW/cm2,θ=60°,ωx=50.54ps-1不变，分别取η等于0.5、0.6和0.7，绘制出了系统总光吸收系数随光子能量ћω变化的关系图。从图中可以看出共振峰的位置并不随光子能量的变化而改变，但总光吸收系数峰值却随着η值的增加而增大。这是因为η值的增加致使偶极跃迁矩阵元Mij增大，所以总光吸收系数峰值也增大，但是η值的变化几乎不影响各能级间的间距，因此共振峰的位置无明显变化。

如图3所示，为了更为全面的反映当θ取不同值时总的光吸收系数随入射光子能量ћω变化的规律，在保持其他参数I=0.1MW/cm2，ωx=50.54ps-1，ωy=55.04ps-1不变的条件下，做出了θ分别取0°、30°、45°、60°和90°时，系统总光吸收系数随入射光子能量ћω变化的关系图。从图中我们可以清晰的看出随着θ值的增加，总吸收系数的峰值在减小。此现象出现的原因是因为当θ角变大时，Mij的值反而减小，因此总光吸收系数峰值减小，当θ=90°时，总光吸收系数减小到零。此外随着θ角的增大，各能级间间距变宽，导致出现蓝移现象。

4 结论

本文研究了在外加倾斜磁场作用的条件下，具有各向异性抛物势GaAs/AlGaAs量子盘的光吸收特性。我们计算并得到了在系统其他物理参数不变的情况下，当分别改变参数ωx、η、θ时，量子盘的光吸收系数随入射光子能量变化的规律。结果表明系统沿x方向上受限势频率ωx、参数η和磁场倾角θ对量子盘的光吸收系数均有着显著的影响。总光吸收系数随着ωx或η值的增加在增大，随着θ值的增加反而减小。此外，当ωx或θ值改变时，总光吸收系数存在蓝移现象。

图1 ωx取不同值时总的光吸收系数随入射光子能量ћω的变化图

Figure 1 The total absorption coefficient as a function of the photon energy for three differentωx

图2 η取不同值时总的光吸收系数随入射光子能量ћω的变化图示

Figure 2 The total absorption coefficient as a function of the photon energy for three differentη

Figure 3 The total absorption coefficient as a function of the photon energy for four differentθ