A Note On Balancing Non-Wieferich Primes
WANG Yi, DING Yu-chen
(1.School of Applied Mathematics,Nanjing University of Finance & Economics,Nanjing 210046,China;2.Department of Mathematics,Nanjing University,Nanjing 210009,China)
Abstract:Let Bn be the n-th balancing number.Recently,Routh proved that for any positive integers k≥2 andn>1,there are ≫logx/loglogx primes p≤x such that p≡1(mod k) and p2) under the assumption of the abc conjecture for the number field is the Jacobi symbol.Dutta,Patel and Ray improved this lower bound to (logx/loglogx)(logloglogx)M for any fixed M.However,we found that their proofs contain some gaps.Although we failed to fill the gaps right now,the lower bound is improved to logx but without the restriction of mod k in this paper,i.e.,we prove that there are ≫logx primes p≤x such that p2) assuming the abc conjecture for the number field
Key word:Balancing numbers;Wieferich primes;abc-conjecture;algebraic integer
A primepis called a Wieferich prime for base a if it satisfies
ap-1≡1(modp2)
(1)
Ifa=2,we just call it a Wieferich prime for simplicity.It is well-known that Wieferich primes are closely related to the first case of Fermat’s Last Theroem[9].Untill now,only two Wieferich primes 1093 and 3511[4]have been found.The primes which are not Wieferich primes are called non- Wieferich primes.It is unknown whether there are infinitely many Wieferich primes or non- Wieferich primes.
Recall that theabcconjecture states that ifa,bandcare integers with (a,b)=1 anda+b=c,then for anyε>0,
max{|a|,|b|,|c|}≪ε(rad(abc))1+ε,

Now,let’s introduce the generalization ofabcconjecture for number fields.Let K be an algebraic number field.It has been conjectured for anyε>0,there exists a positive constantd(depending only onand K ) such that for any elementsa,bandcofK*witha+b=c,we have
HK(a,b,c)≤d(radK(a,b,c))1+ε
The definitions ofHK(a,b,c) and radK(a,b,c) can be found in [10] and we just omit them here as we do not need them in the present paper.
Panda[5]defined the balancing numbersn∈+to be the solutions of the equation
1+2+…+(n-1)=(n+1)+(n+2)+…+(n+m)
for some natural numberm.LetBnbe then-th balancing number with the first two beingB1=1 andB2=6.Balancing numbers has the recurrence relationBn+1=6Bn-Bn-1forn≥2.Indeed we can find the closed form of balancing number satisfy

Let P be the set of all primes.We state our main result in the following.

1 Remarks of the balancing non-Wieferich primes in arithmetic progressions
Both articles mentioned above used the following lemma which is a classical result of the cyclotomic polynomialΦn(x),however,not true for general algebraic integers.
Lemma1.1[4]Letn≥1 be a positive integer andb≥2 be an integer.Ifpis an odd prime withp|Φn(b)|,then eitherp|norp≡1(modn).



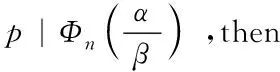
for somel∈.So we have

2 Some lemmas


(2)
Lemma2.1[7]Balancing numbers satisfy the inequalityαn-1 Form Proof:By Möbius inversion formula ofφ(n),we have It is clear that It is easy to see that Hence,by Lemma 2.4,we have whereWis the same as in Lemma 2.5.By Lemma 2.1,we haveX2n #{n:n∈S,X2n≤x}≥#{n:n∈W,α2n≤x} Finally,we obtain that The second author would like to thank Professor Haiyan Zhou in Nanjing Normal University for her generous help and encouragement all the time.Proposition 1.1 is suggested by Professor Hao Pan in Nanjing University of Finance & Economics.We would like to thank him for allowing us to use it in this article.Last but not least,many thanks to Dr.Guilin Li and Liyuan Wang in Nanjing University for their helpful comments during the writing of our paper.
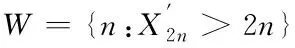
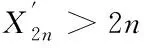
3 Proof of Theorem 1


Acknowledgment

