变极距长初级双边直线感应电机磁场及电感研究

刘希军，刘小涵，高丽霞

(中国民用航空飞行学院 航空工程学院，四川 广汉 618307)

0 引 言

对于电磁发射系统，直线驱动电机是驱动的动力源，亦是核心部分，直线电机可以直接将电能转换成直线运动形式的机械能[1-2]。直线电机驱动的传动装置，无中间转换机构，可直接产生推力，系统装置简化，即可以保证运行的可靠性，亦可以降低制造成本，便于维护。

直线电机驱动装置驱动过程中，电能直接转换成电磁推力，且运动过程中可以无机械接触，传动零部件无磨损，很大程度上减小了机械损耗[3-4]。直线电机驱动过程无机械接触，没有旋转电机传动过程中，钢绳、齿条、传送带等中间转换机构产生的噪音污染。直线电机驱动负载做直线运动，结构紧凑，运行效率高，长定子短动子的结构使动子较轻，更适合于高速大推力的运动场合。

1 变极距直线感应电机气隙磁场分析

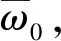
(1)

假设任意一对极中，第i个极距的大小为i，则与其相邻的下一个极距大小为i+1，每个相带的宽度依次递增恒定值各个相带宽度如图1所示。

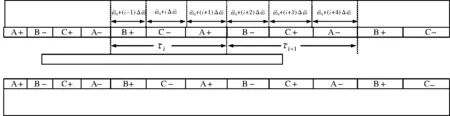
图1 等变相宽度型变极距直线感应电机模型

假设第i个极距前电机速度为vi，则由牛顿运动学定律可知

(2)

(3)

对于任意极距而言，均对应半个周期，因而式(3)与式(2)做差值可得

(4)

因而，式(1)可整理为

(5)

式中，a为加速物体加速度值；f为电源供电频率。

物体在加速的过程中，由于前部空气被压缩，两侧面空气的摩擦，以及后部空间部分真空等因素，引起空气阻力[6-8]。其中空气粘度在加速物体表面产生的切向摩擦力所占空气阻力比重较小，暂且忽略[9-11]。空气阻力的大小和速度的平方成正比关系，速度越大，空气阻力越明显，运动的物体所受空气阻力可表示为

(6)

式中，C为空气阻力系数，其值的大小主要和物体的迎风面积、物体的形状和光滑程度有关，垂直平面体风阻系数约为1.0，球体风阻系数约为0.5，轿车风阻系数约为0.28～0.4，飞机风阻系数约为0.08；ρ为空气密度，干燥空气密度为1.293g/l；S0为物体迎风面的面积；v为物体与空气的相对运动速度。

物体高速运动考虑空气阻力时，提出两种分析方案。保持物体在整个加速过程的加速度不变，即电磁推力随着速度的增加而增大，以克服空气阻力，因而需改变初级线圈绕组中电流大小以增大电磁推力输出，必然需要不断的实时检测物体的运动速度状态，并进行闭环反馈控制，无疑会增加控制难度，与系统所提出的变极距简化控制方式思想背道而驰，因而未采取本方案。另外可以依旧保持电磁推力输出不变，此时，由于空气阻力的存在，物体将做减加速运动，根据牛顿运动学公式可推导出，考虑空气阻力作用时，物体的加速度为

(7)

式中，Fem为电磁推力输出；M为被加速物体质量；s为物体运动位移。

(8)

(9)

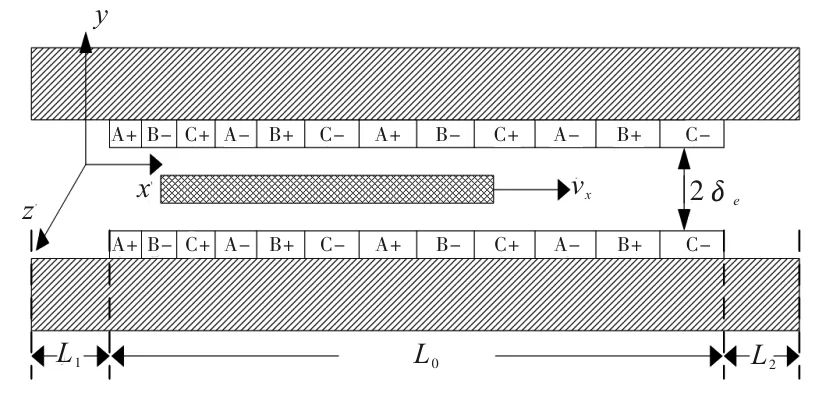
图2 变极距直线感应电机解析模型

在电机实际运行时采用分段供电模式，因而假设通电段初级绕组的长度为L0，通电段极数为p，未通电段初级绕组的长度分别为L1和L2。变极距直线感应电机解析模型如图2所示。x轴为行波磁场方向，y轴为磁动势方向，z轴为线圈绕组中电流正方向。

分析A相绕组，仅当A相绕组通电时，不同区域、不同相宽的磁动势关系为

(10)

式中，Ai为i区域的磁动势；N为线圈匝数；iA为A相电流值；端部两个极的安匝数为NiA/2，中间各极下的安匝数为NiA。

由式(6)可以求得

(11)

对于任意任意位置x所在的区域区域ki而言，其磁动势为

(12)

式中，Jki为ki区域的线电流密度。

(13)

根据不同区域磁通量的连续性可知

(14)

式中的通电段初级绕组长度L0表示为

(15)

据此可求取仅A相通电时，电磁气隙标号i区域的磁通密度表达式为

(16)

(17)

(18)

对于任意位置x所在的区域ki而言，其磁通密度表达式为

(19)

2 变极距直线感应电机自感互感计算

2.1 绕组自感计算

A相绕组的自感磁链为

(20)

A相绕组的自感为

(21)

式中，2d为次级厚度。

B相绕组的自感磁链为

(22)

B相绕组的自感为

(23)

C相绕组的自感磁链为

(24)

C相绕组的自感为

(25)

2.2 绕组互感计算

当A相绕组通电时，B相绕组铰链的磁链为

(26)

A相和B相绕组之间的互感为

(27)

当A相绕组通电时，C相绕组铰链的磁链为

(28)

A相和C相绕组之间的互感为

(29)

当B相绕组通电时，C相绕组铰链的磁链为

(30)

B相和C相绕组之间的互感为

(31)

根据变极距直线感应电机各项绕组自感、互感计算公式可以分析，由于极距变化，使得互感参数之间均互不相等，这主要是由于各相与行波磁场交链的磁链不同造成的。

定义脉振偏置磁场电感参数为

(32)

脉振偏置磁场电感对三相绕组之间的互感值均有影响，且其电感值与相带宽度递增值成正比，与等效气隙成反比，并于通电段绕组所占总初级长度的比例成正比关系。

3 极距变化对电感和磁场影响

根据各相绕组单独通电时的磁感应强度值，可得各相绕组的自感磁链值、铰链磁链值，进而求得各相绕组的自感值和绕组之间的互感值。

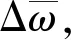
图3 供电频率对A相绕组自感值影响

图4 供电频率对B相绕组自感值影响

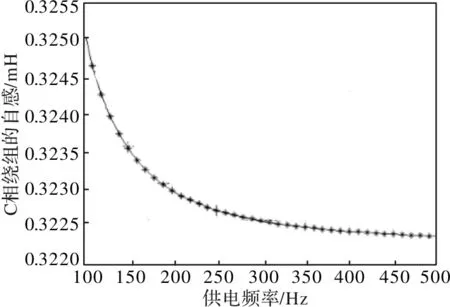
图5 供电频率对C相绕组自感值影响

图6～图8给出了不同供电频率下三相绕组的互感值。

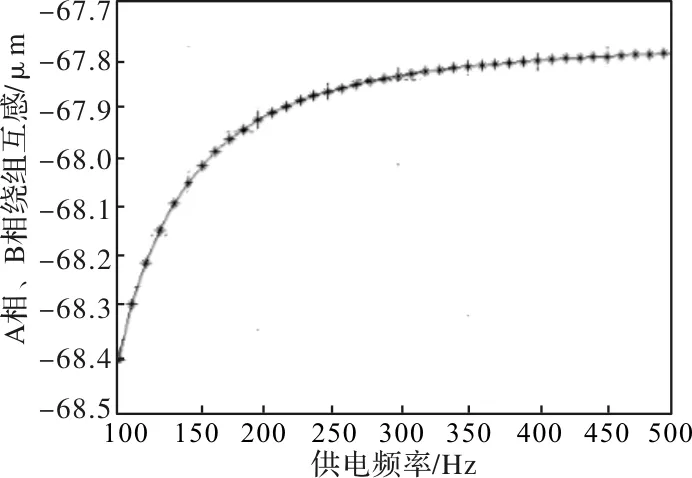
图6 供电频率对A相、B相绕组互感值影响

图7 供电频率对A相、C相绕组互感值影响

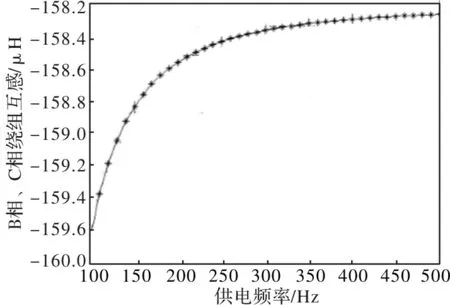
图8 供电频率对B相、C相绕组互感值影响

从图中分析可知A相、C相绕组互感值和B相、C相绕组互感值近似相同，而A相、B相绕组互感值则相对较小，这主要是因为三相绕组物理排布的不对称导致A相或者B相单独通电时，其它两相交链的互感磁链不同。三相绕组互感值整体均随供电频率的增加而呈现增大趋势，当频率较高时，互感值趋于恒定值。

图9和图10分别为不同电机极距的情况下，x轴方向和y轴方向磁感应强度变化情况。

从图中分析可知，对于变极距直线感应电机而言，在系统运行过程中，随着速度的不断增大，电机极距的不断增加，x方向磁感应强度呈线性增大趋势，y方向的磁感应强度线性减小。

图9 x方向磁感应强度随电机极距变化曲线

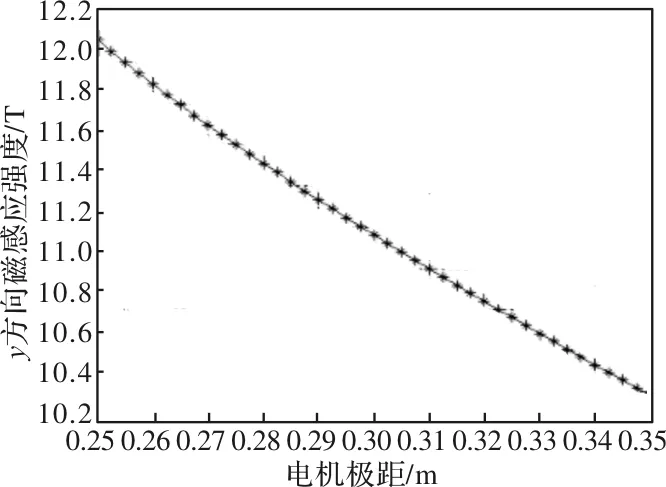
图10 y方向磁感应强度随电机极距变化曲线

4 结 语

在分析变极距直线感应电机时，将变极距模式拓展为变相宽度的形式，求取任意位置所在的区域的磁感应强度表达式，计算推导变极距电机各项绕组的自感、互感公式，并仿真分析极距的变化对电机电感特性的的影响，得到结论如下：

(2)由于三相绕组物理排布的不对称导致某相单独通电时，其它两相交链的互感磁链不同。三相绕组互感值整体均随供电频率的增加而呈现增大趋势，当频率较高时，互感值趋于恒定值。