基于无人直升机的舵机建模与控制律设计

孙 宾，应 浩

(南京模拟技术研究所，南京210016)

0 引 言

舵控系统由舵机控制器和舵机组成，作为无人直升机上执行机构的控制系统，其性能直接影响飞行品质与飞机安全[1]。舵机作为舵机控制器的控制对象，飞行过程中实时调整飞机舵面，确保飞行姿态平稳。舵控系统在完成对舵机丝杆位置精准控制的同时，需要最大化的实现安全控制裕量[2]。

本文研究的舵机由空心杯稀土永磁直流无刷电动机、减速箱、滚珠丝杆、高精度电位器等子部件组成。其工作原理为飞控计算机将接收到或计算出的飞行姿态，进行姿态闭环，得到当前时刻舵机丝杆应达到的位置需求，舵机控制器接收到该指令后，进行位置闭环，控制电机转速，电机齿轮经由减速箱，带到滚珠丝杆运动，最终实现舵面位置控制要求[3-5]。

1 舵机建模

无人直升机由于没有降落伞、缓冲垫等保护措施，如果发生飞机姿态等异常情况时，电动舵机绝对不能失电，必须要求舵机保持位置精度，因此在电机控制回路中，只进行电流信号的采集与监控，不考虑电流环设计。为满足位置精度要求，本设计采用位置环与转速环，其中转速环为内环，位置环为外环，其控制模型如图1所示。

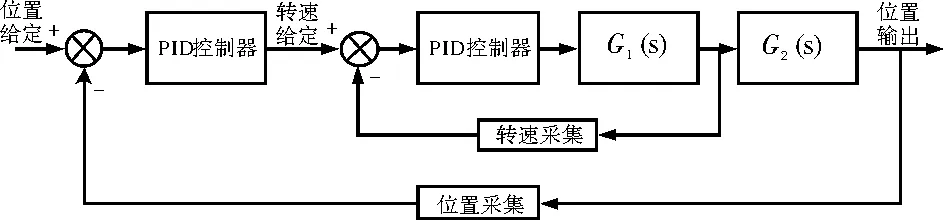
图1 舵机控制回路模型

无人直升机上舵回路电机相关电气指标应按照气动力学的载荷要求和飞机的动态特性进行选取，该部分不在本设计的讨论范围内，在此不做赘述。本设计所选取的电机为空心杯稀土永磁直流无刷电动机。其中，舵机齿轮减速比为2.8；丝杆导程为3.1mm。

根据电机将电能转换为机械能的工作原理，联立方程如下：

(1)

式中,U(t)为当前某时刻系统供电电压；E(t)为当前时刻电机的反向电动势；i(t)为当前时刻电机上电流；L为电机电枢电感；R为电机相间电阻。

电机的反向电动势表达式为

E(t)=Ce×ω(t)

(2)

式中，Ce为电机反电动势系数；ω(t)为当前时刻测得的电机转速。

电机的电磁转矩表达式为

Tm(t)=Cm×i(t)

(3)

式中，Cm为电机电磁转矩系数。

电机的转子为一圆柱体，因此其转矩方程为

(4)

式中，Jm为圆柱体绕垂直于圆面中心轴的转动惯量，其表达式为

Jm=M×r2/2

(5)

式中,M为电机转子质量；r为转子圆柱体圆截面半径。

将系统供电电压作为输入量，将电机转速ω作为输出量，联立式(1)～式(4)，得出：

(6)

直线舵机在计算丝杆运行速度时，需要将电机的旋转运动转换成舵机丝杆的直线运动，其转换公式为

(7)

式中,β为直线舵机的减速箱齿轮减速比；D为舵机丝杆的导程。

舵机丝杆的直线运行速度V(t)与位置P(t)成积分关系，因此，位置传递函数为

(8)

联立式(6)与式(8)，可得舵机传递函数为

G(s)=G1(s)×G2(s)

(9)

相间阻抗、电枢电感、电机反电动势系数、电机电磁转矩系数等计算公式此处不做赘述[6]。

电机相关技术参数如表1所示。

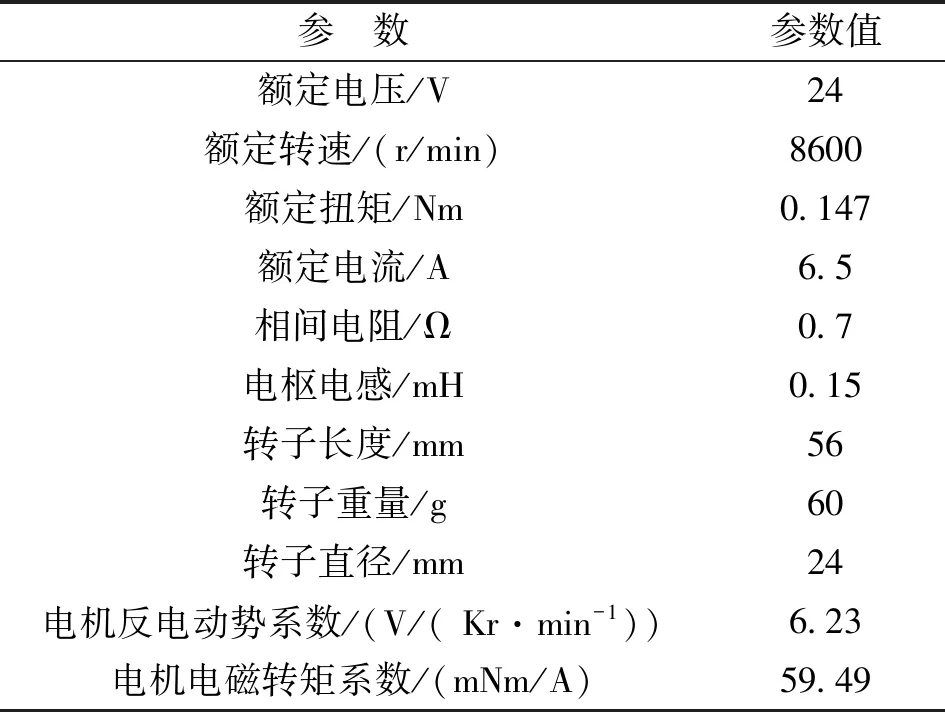
表1 电机参数

2 控制律设计

舵机控制方法不同于其它控制系统，正常控制过程中，当舵机丝杆运行到指定位置后，需要舵机控制器释放掉控制量，即PWM的占空比输出0；否则电机会持续转动，轻则造成电机堵转，重则造成舵机丝杆在指定位置附近振荡，进而影响飞机姿态与飞行品质。但控制量释放掉后，旋翼的下旋压力会压迫舵机丝杆运动，造成舵机丝杆不能精准定位在指定位置。因此在控制律设计之初，需要摸清电机起动电压、位置传感器精度等信息。

简化后的舵机控制回路模型如图2所示。各个模块的原理分析如下：

(1)死区设置，当舵机丝杆运行到指定位置附近，满足位置传感器精度误差范围时，将舵机控制量释放掉，在一定程度上可减少舵机抖舵，且减少电机的发热量。大载荷、长航时等严苛环境下，该情况特别明显。

(2)Con模块为一常量，该常量的取值依据为电机的起动电压，增加该环节的优点是，当舵机丝杆位置偏差err超过死区时，立刻能使电机动作，减少堵转电流的同时，可明显较少位置误差。

(3)Kp为位置误差的比例项，该值的大小直接影响舵机丝杆的运行速度与舵机带载能力；

(4)Ki*Sgn为位置误差的积分项，用于减少位置误差，只有在满足位置误差范围条件内，才实现对位置误差的累积，大行程时，该项不使用，且有积分限幅要求；

(5)Kd作为速度环的比例项，同时也是整个系统控制率的阻尼项，该值选取时需根据实际使用情况进行处理；

(6)Kp*s为前馈项，其为位置指令变化率的比例项，该前馈项的引入对整个时变系统的位置误差起到很好的抑制作用，且能提高整系统的频率响应。

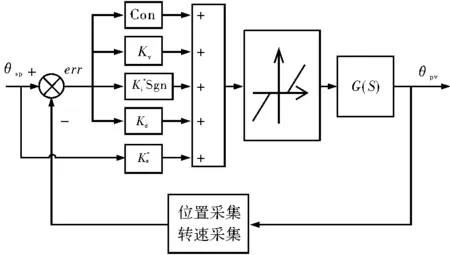
图2 简化后控制回路模型

3 舵机控制器设计

舵机控制器主要完成接收舵机位置指令、采集当前舵机丝杆位置、舵电机转速、电流以及控制律实现与控制量输出、光耦隔离、电机驱动、故障点检测、信息上传等功能。其原理框图如图3所示。

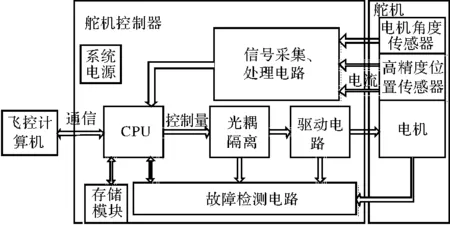
图3 舵机控制器原理框图

4 试验结果与分析

根据模型的建立与控制律的设计，配合舵机控制器，进行实物测试，分为桌面扫频试验与机上飞行试验。

4.1 扫频试验结果及分析

扫频试验工作原理为：给舵机控制器施加变频变幅指令，在200 s时间内频率从0.05 Hz渐变到6 Hz，幅值为总行程的±5%，扫频结果如图4所示。

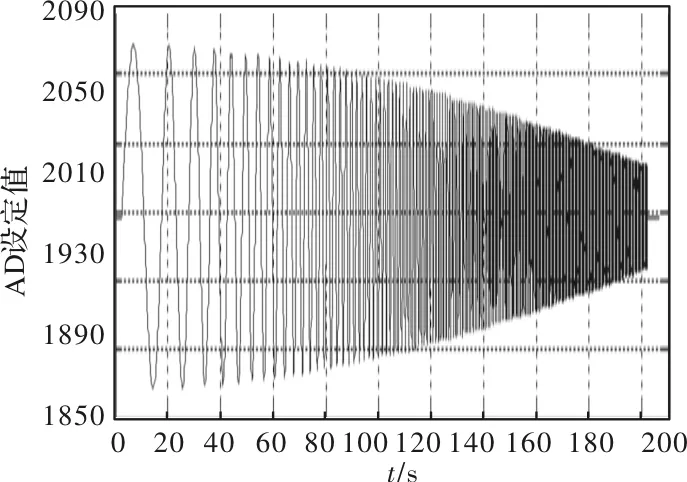
图4 6Hz正弦信号响应图

观察图4发现，反馈值可以很好的跟随设定值，位置幅值基本无衰减，其伯德图，如图5所示。

图5 系统伯德图

从图5可以分析得出，在舵机控制系统的频响达到1秒37.7弧度时，系统相干性大于0.6，在此范围内，幅值基本没有衰减，相位滞后约为70°。满足无人直升机舵机控制器带宽为整机控制带宽(0.7 Hz左右)3～5倍的要求。

4.2 飞行试验结果及分析

在正常的飞行过程中，飞机姿态是时变的，但又不会发生太大的变化量，因此对舵机在较短时间内的响应要求很高，既要快速响应指令要求，又要满足位置精度要求，图6为某一次完整的飞行数据，总距的设定与反馈信息如图6所示。

图6 一次完整的飞行数据

从图6数据可以得出，无人直升机在实际飞行过程中其各个舵机是处于小范围、时变运行环境下，其反馈可以很好的跟随设定，且设定与反馈的差值，最大为1%，在满足及时响应指令要求的同时，可以很好的达到位置精度指标。

5 结 语

为尽量提高无人直升机中舵机控制系统的工作带宽，本文从推理舵机的建模方法、详细叙述改进型PID控制律的设计方法和舵机控制器的原理设计等三个方面进行说明，最后对大量的扫频与飞行试验进行数据分析，结果表明：舵机控制系统在6 Hz的频响条件下，幅值衰减小于0.5dB，相位滞后约70°，完全满足实际飞行需求。