永磁同步直线电机DDPG自适应控制

张振宇，张 昱，陈 丽 ，张东波

(1.沈阳工业大学 信息科学与工程学院，沈阳 110870；2.广东省智能制造研究所 广东省现代控制技术重点实验室，广州 510070)

0 引 言

永磁同步直线电机(Permanent Magnet Synchronous Linear Motor，PMSLM)有着推力大、速度大、行程大和精度高等优点，因此广泛应用于现代工业中[1]。直线电机伺服系统相比传统的伺服电机精简了机械结构，取消了传动环节，具有优越的加减速度特性和高刚度、高可靠性，运行噪声小，维护简单等优点。目前，直线电机技术已经比较成熟，并越来越多地用在高速、高精密机械加工中[2]。由于实际直线电机伺服系统的非线性及不确定性，当模型的不确定性超过传统线性最优鲁棒控制所允许的范围时，控制系统就变得不稳定[3]，所以传统PID控制在直线电机高加速运行有干扰情况下不能达到理想的控制效果。

针对以上现状，为了在高速高精度应用场合实现对非线性、强耦合、负载扰动大的永磁同步直线电机的快速精准控制，本文提出深度确定性策略梯度(Deep Deterministic Policy Gradient , DDPG)算法自适应控制策略，其被控对象可以是非线性系统，DDPG自适应控制系统基于强化学习，具有很强的自学习、自整定能力，能根据负载扰动进行更新控制策略，有效提高系统抗干扰能力，减小速度信号跟踪误差。并通过在Matlab/Simulink仿真平台仿真分析和传统PID控制性能进行对比实验，验证DDPG自适应控制器的动态性能。

1 永磁同步直线电机模型建立

为了分析直线电机的特性，并在Simulink上进行仿真，首先要对直线电机进行数学建模。直线电机的数学模型是个强耦合、多变量、非线性系统，直接分析它的微分方程难度很大，通常釆用的方法是坐标变化方法[4]。将三相正弦交流电通入交流电机定子的三相绕组A、B、C中，会产生旋转磁势，它在空间是呈正弦分布的。为了分析和设计的方便，直线电机数学模型通常需要用到Clark变换、Park变换和Park逆变换。

将三相静止坐标等效为两相静止坐标(3S/2S)，ABC→αβ0，称为Clark变换。

(1)

考虑零轴分量，两相αβ坐标系到两相dq坐标系的变换矩阵形式为：

(2)

通过矢量旋转变换，将两相静止的αβ坐标系变换到两相旋转的dq坐标系，称为Park变换。经过变换后，PMSLM的d、q轴数学模型模块如下：

电流平衡模块：

根据矢量控制的基本原理，可以推出直线电机在d、q轴数学模型下的电压方程式为

(3)

式中，Rs为初级绕组等效电阻，ud为直线电机d轴电压，id为d轴电流，ψd为d轴磁链；uq为q轴电压，iq为q轴电流，ψq为q轴的磁链；为永磁体极距，v为直线电机的同步运动速度。

磁链方程为

(4)

式中，Ld为d轴电感，Lq为q轴电感，ψf为永磁体励磁的基波磁链。

电磁推力方程为

Fe=K[ψfiq+(Ld-Lq)idiq]

(5)

(6)

式中，Fe为电磁推力系数。

机械运动方程：

(7)

式中，M为直线电机初级的质量，F1为负载干扰阻力，B为黏性阻力系数。

因为直线电机的次级为永磁体，由式(6)知，当初始状态保持iq与d轴垂直，不仅可以对直线电机数学模型进行参数解耦，而且还可以得到最大推力。所以采用id=0的矢量控制策略，则永磁同步直线电机的数学模型可简化为

(8)

所以直线电机传递函数结构图如图1所示。

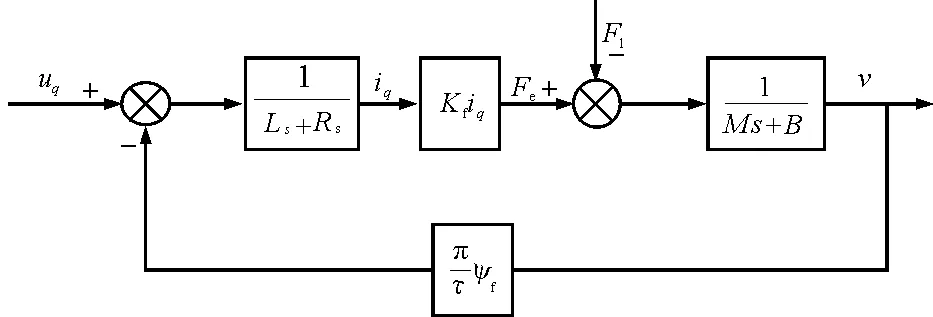
图1 直线电机传递函数结构图

根据上述直线电机数学建模在Simulink上搭建好直线电机模型，由于直线电机采用脉宽调制的三相电流供电，并采取电流跟踪控制的，所以需要在直线电机模型前再连接SVPWM模块，而DDPG自适应控制器是根据控制电流跟踪，来实现直线电机模型控制的。

2 DDPG自适应控制策略

DDPG是深度强化学习的一种算法，是一种数据驱动的控制方法，可以根据系统的输入输出数据，学习系统的数学模型，并根据给定的奖励实现系统的最优控制。2013年，Deep mind公司提出了深度Q网络(Deep Q-Network, DQN)。通过将DQN应用到视频游戏，强化代理仅通过从图像中获取信息多次训练，就可以就能熟练的闯关游戏[5]。Lillicrap 等人于2015年提出了一种深度确定性策略梯度(DDPG)算法作为重放缓冲器来构建目标网络，以解决连续运动空间神经网络收敛和慢速算法更新的问题[6],并在Nature上发表的关于深度强化学习的论文[7]。

DDPG算法是一种无模型、在线、离线策略的强化学习方法，仅利用受控系统的输入输出数据直接进行控制器的设计和分析，使用批量次的数据对仿真代理进行训练，最终培训出合适的强化代理，在强化代理根据环境改变而更新策略，来更新评判Q值。DDPG采取经验回放机制，通过连续对目标网络参数与当前网络的参数加权平均进行训练，以避免振荡[8]。

深度强化学习具有良好的知识转移能力，这对于伺服系统跟踪具有不同幅度或频率的信号是必要的。DDPG是一种数据驱动的控制方法，可以根据系统的输入输出数据学习系统的数学模型，并根据给定的奖励实现系统的最优控制。通过DDPG的自学习智能结构，提高直流电机伺服系统精度[9]。

DDPG自适应控制器基本框架如图2所示。

图2 DDPG自适应控制器基本框架图

图中虚线上部分是基于强化学习的自适应参数调节器，由强化学习代理组成，虚线下部分由被控对象组成作为代理环境交互对象。其中误差e(t)=u(t)-y(t)，u(t)是初始输入值，y(t)是反馈值。

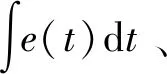
考虑到系统误差和反馈值数值范围对系统控制性能的影响, 奖励函数定义为

rt=α1r1(t)+α2r2(t)

(9)

其中,α1,α2分别为限定误差值范围和反馈数值范围的奖励系数,r1(t)，r2(t)分别为误差值范围和反馈数值范围，定义为

(10)

(11)

其中，σ为允许的误差带，y′(t)为反馈数值上限。

在Simulink上搭建的基于DDPG自适应控制器的直线电机速度环控制框图如图3所示。

图3 DDPG自适应直线电机速度环Simulink控制框图

V0为初始给定速度模块；C_npmlsm为直线电机电流环集成模块；Signal Processing为直线电机对强化代理的信号处理模块，以直线电机的速度误差e和反馈速度Velocity信号作为输入，再将速度误差e、误差积分及反馈速度Velocity作为观察状态st输入到强化代理的观察状态Observation端口，反馈速度Velocity的速度范围作为强化代理的截至范围输入到强化代理的Isdone端口，根据对误差e的限定范围及反馈速度截至范围设定的奖励输入到强化代理的Reward端口；RL Agent为DDPG强化代理模块，将动作值作为直线电机电流环的输入电流值输入到C_npmlsm模块中。

DDPG自适应控制器在Simulink上搭建大部分需要采用M文件下编写S函数来调用神经网络模块组建强化学习代理。

3 实验结果与分析

基于DDPG自适应控制器的直线电机速度环控制系统在Simulink上搭建好以后，将主要相关参数输入。本论文仿真参数设置为Rs=3.3 Ω,Ld=Lq=0.001 H,M=1 kg,B=1.2 N·s/m,ψf=0.23336Wb,=0.048 m,连续推力F1=130 N。给定速度设置为2 m/s，奖励函数设置为rt=5×(e<0.01)-1×(e>0.01)-100((y′(t)>4)‖(y′(t)<0))。在强化代理经过多回合自学习，自整定后，当训练的指标达到设定的指标时，仿真模型停止训练，并生成最优强化代理，保存到指定的文件夹下。

仿真速度初始给定2 m/s，在无干扰条件下，传统PID控制和DDPG自适应控制的速度对比仿真结果如图4所示，从图中的对比波形图可看出，DDPG自适应控制不仅超调量小，而且具有更快的响应速度。

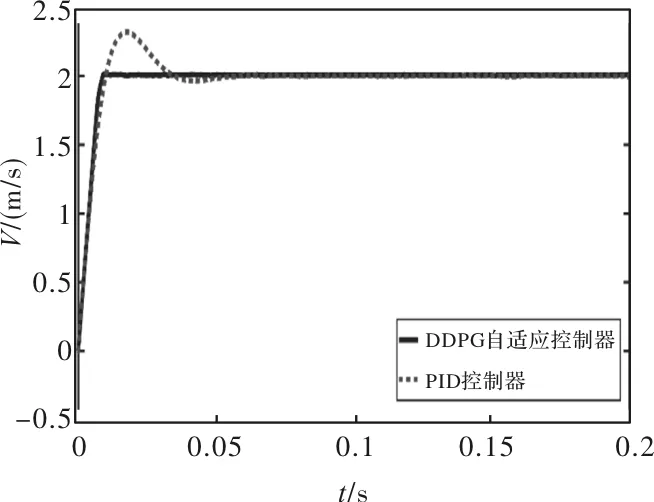
图4 无干扰速度对比仿真波形图

为了检验系统的抗干扰能力，仿真速度初始给定2 m/s，在t=0.1 s时，施加50 N的负载扰动，传统PID控制和DDPG自适应控制的速度对比仿真结果如图5所示，从仿真图中速度波形可看出，DDPG自适应控制相比PID控制，不仅减小了超调量，提高了系统的响应速度，而且在被控系统突加扰动的情况下，扰动小，能使系统快速恢复稳定，具有较强的抗干扰能力。

图5 施加干扰速度对比仿真波形图

为了检验系统的跟随性能，仿真速度输入为方波信号，初始速度为1 m/s，在t=0.08 s时，变为4 m/s，在t=0.16 s时，变为2 m/s，在t=0.24 s时，变为1 m/s，在t=0.32 s时，变为3 m/s。传统PID控制和DDPG自适应控制的速度对比仿真结果如图6所示，从仿真图中速度波形可看出，DDPG自适应控制相比PID控制，具有更优良的跟随性能。

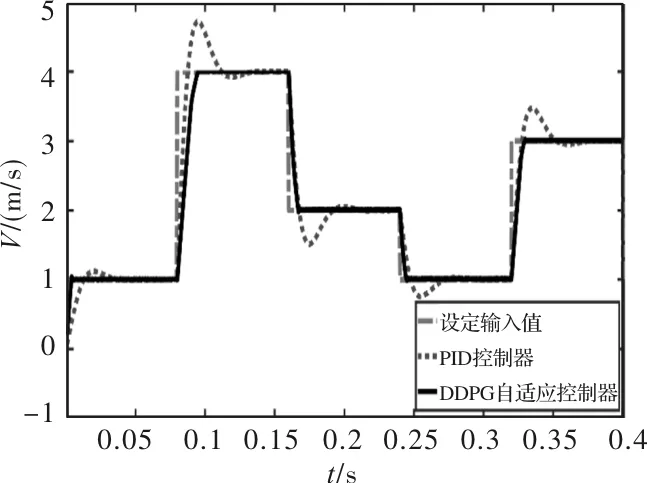
图6 跟随速度对比仿真波形图

4 结 语

本文针对直线电机的模型的非线性、强耦合、负载扰动大等特点，提出了一种基于DDPG自适应控制新型控制方法，应用于PMLSM的速度控制环中。DDPG自适应控制器强化代理是在Actor-Critic网络基础上建立的，Actor网络实现了策略的最佳近似，Critic网络实现了价值函数的最优逼近，采用参数随机OU噪声动态调整等策略，提高了神经网络的收敛速度，同时提高了控制系统的精度。

本文利用Matlab/Simulink软件包中现有的工具和库，对PID控制器和DDPG自适应控制器的性能进行了比较研究，并通过不断在Simulink上仿真训练，优化DDPG自适应控制器。模拟仿真后，实验结果表明：DDPG自适应控制器可以实现对非线性系统的稳定跟踪控制, 并且与传统的PID控制相比, 基于DDPG自适应控制器控制器具有响应速度快, 自适应能力强, 抗干扰能力强，跟随效果好等优点。