开关磁阻电机初始位置的高精度检测

陈 强，韩润宇，孙建忠

(1.中车永济电机有限公司，山西 永济 044502；2.大连理工大学，辽宁 大连 116023)

0 引 言

开关磁阻电机是兼具直流传动与交流传动优点的机电一体化调速系统，在各种需要调速和高效率、高可靠性运行的场合受到了普遍关注。位置闭环控制是开关磁阻电动机的基本特征，但是位置传感器的存在使电机的结构变得复杂，同时也降低了电机的运行可靠性。为此探索实用的无位置传感器控制方案是十分必要[1]。

国内外研究人员对开关磁阻电机的无传感器控制进行了深入的研究，通过开关磁阻电机的绕组电感、电流和磁链与转子位置角之间的映射关系，来间接检测开关磁阻电机的转子位置信息[2-3]。高频脉冲注入法是一种适用于低速和起动的检测方法。文献[4]分析了开关器件和电机产生的各种干扰对注入脉冲的响应电流峰值的影响，提高了脉冲注入法的位置检测精度。文献[5-6]给出了无位置传感器控制时初始起动相的判断方法，在电机静止时，向每一相绕组都注入短时高频脉冲，根据响应电流峰值的大小关系，确定初始启动相。文献[7]通过对注入脉冲的响应电流峰值与设定的阈值进行比较，产生换相信号，从而提高转子位置检测精度。

无位置传感器启动时，电机的初始位置判断十分重要，但现有的无位置传感器控制方法大多只判断初始位置的扇区，无法计算其精确位置。也有人在电机起动前，采用单相通电的方法，使转子吸合到特定位置，这种方法在很多应用场合是不可行的。本文在高频脉冲注入法的基础上，提出了一种精确估算转子初始位置的方法。

1 高频脉冲注入法

高频脉冲注入法的基本原理是：在开关磁阻电机单相运行时，向非导通相注入一定占空比的高频脉冲信号，根据高频脉冲的电流响应，判断转子位置角。

向非导通相注入幅值为U的高频脉冲电压时，绕组电流i与电压U之间的关系为

(1)

式中，R为一相绕组的电阻；L为一相绕组的电阻；Ω为转子的角速度；θ为转子的位置角。

(2)

当通电时间足够短时，可使绕组在高频脉冲的每个通电周期都完全放电，则电流的初始值为0，式(2)可以写为

(3)

式中，ip为响应电流的峰值，Δt为一个周期内脉冲注入的时间。

绕组电感L是转子位置角θ和绕组相电流i的函数。在电流较小、且磁路不饱和时，可近似认为绕组的相电感是转子位置角的单值函数，因此通过检测非导通相绕组的响应电流峰值，就可以间接估计电机的转子位置角。

2 初始位置的精确计算

2.1 高精度初始定位方法

根据开关磁阻电机的电感特性，可将一个通电周期平均分为6个扇区，各相绕组的导通扇区各不相同，如图1所示。观察图中三相绕组的电感曲线可见，从转子极与定子极开始重合的位置到转子极与定子极完全重合的位置，电感几乎随着位置变化呈线性变化。在任意扇区中，三相电感曲线处于中间位置的一相电感变化线性度极高，可以利用这一特性，进行精确的转子定位。

图1 三相绕组电感与精确定位

与传统的初始定位方法相比，此方法不仅可以知道转子位置扇区，还可将转子位置进一步精确。由于三相绕组的对称性，6个扇区对应的电感特性的直线段顶点的电感相等，因此只需预知两个交点位置处的电感值，即可求得任意扇区任意位置的位置角。

2.2 响应电流波形校准

由于实际的电流传感器及运算放大器均存在一定的零点偏移以及增益误差，并且不同传感器和放大器存在个体差异，使得检测到的三相响应电流峰值的放大值之间存在较大的偏差。为使三相响应电流峰值与对称，必须对检测到的三相响应电流峰值进行校准。

简化电流传感器以及运算放大器的误差模型，认为仅存在零点偏移以及增益误差。以A相响应电流峰值为基准，对三相响应电流进行校准，校准公式如下

(4)

式中，xA、xB和xc分别为未校准前的实际检测值，yA、yB和yC为校准后的值，kB和kC为校准斜率项，bB和bC为校准截距项。

根据不同转子位置下三相绕组的响应电流峰值，绘制三相响应电流峰值随转子位置角变化的波形。以A相响应电流峰值随转子位置角变化的波形为基准，将A相响应电流峰值波形向左移动120°电角度，作为B相响应电流峰值随转子位置角变化的校准波形，对B相响应电流峰值进行最小二乘法线性拟合得到kB和bB；然后将A相响应电流峰值波形向左移动240°电角度，作为C相响应电流峰值随转子位角变化的校准波形，对C相响应电流峰值进行最小二乘法线性拟合，得到kC和bC。

2.3 转子位置角的精确计算

从转子极与定子极刚开始重合的位置到转子极与定子极完全重合的位置，电感随位置角近似呈线性变化。在任意一个区间内，三相电感曲线中，处于中间的一相电感曲线的线性度最高。可以利用这一特性，进行精确的转子定位。

当注入脉冲的电压、频率和占空比均不变时，响应电流峰值ip与相电感L成反比关系。因此，可用响应电流峰值ip的倒数与位置角的关系来模拟相电感L与位置角的函数关系。

两个交点处的电感可通过给电机进行单相或两相通电定位的方法获得。对A相绕组通电，将转子吸合至A相的对齐位置，停止通电后保持转子位置不动，对B、C两相进行高频脉冲注入，求取其校正后的电流峰值的均值，其倒数可作为交点E处的计算电感值Ls。对A、B两相同时通电，将转子吸合至C相不对齐位置，停止通电后保持转子不动，对A、B相进行脉冲注入，求取其校正后的电流峰值均值，将其倒数作为交点D处的计算电感值Ll。

对校准后的响应电流峰值求倒数，得到计算电感L，比较响应电流峰值的大小，判断转子所在扇区，精确的转子位置计算公式如表1所示。

表1 转子位置计算公式

2.4 扇区判断

由式(3)可知，当脉冲电压和通电时间一定时，响应电流峰值与绕组的电感成反比。因此，在电机静止时，对三相绕组同时注入高频脉冲，其响应电流峰值与电感的关系如图2所示，转子位置所在扇区可由表2所示的关系判断。表中，iA、iB、iC分别为A、B、C三相绕组对注入脉冲的响应电流峰值。

图2 绕组电感扇区与响应电流峰值的关系

表2 响应电流峰值与扇区判断

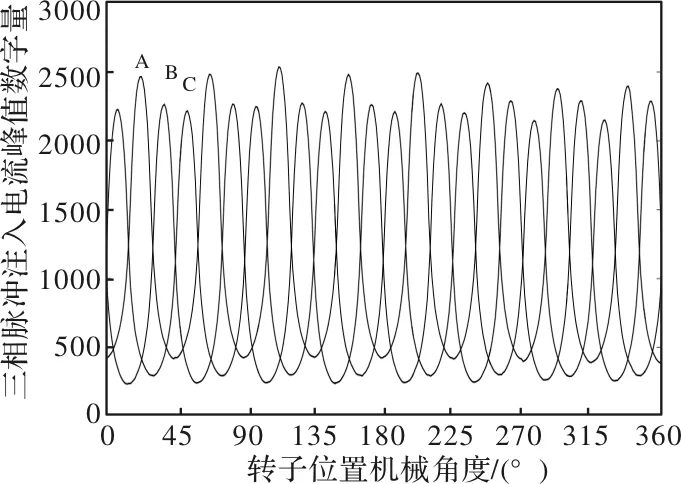
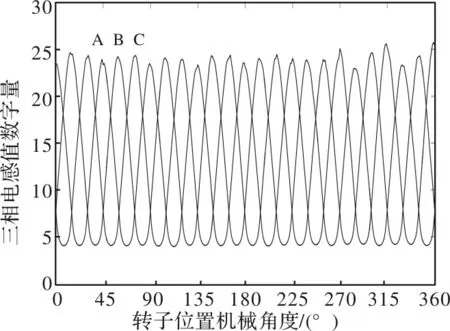
响应电流峰值关系转子位置角扇区iA

3 实 验

采用TI的32位单片机TMS320F28069为控制核心，构建开关磁阻电机的无位置传感器控制系统如图3所示。通过向非导通相注入短时高频脉冲来检测转子位置，实现位置计算和转速计算，从而构成转速、电流双闭环控制系统。为了提高响应电流峰值的检测精度，通过硬件放大电路对响应电流的峰值进行放大。

图3 开关磁阻电机无位置传感器控制系统框图

在确定电机的初始位置时，为使电机转子保持不动，通过三相不对称半桥功率变换器向三相绕组同时注入固定占空比的高频电压脉冲时，控制所注入脉冲的占空比的大小，使电机产生的电磁转矩小于总阻力转矩。

实验样机是一台额定功率为4kW、额定电压60Vdc、额定转速3000r/min的三相12/8极开关磁阻电机。为了验证转子位置检测精度，在电机轴上安装了位置刻度盘，其测量精度为0.1°，以刻度盘所指示的位置角作为实际位置角。

图4 未校准的三相响应电流峰值

图5 校准后三相响应电流峰值

测得的三相响应电流未校准前的数字量如图4所示，可见三相响应电流波形对称性较差，必须进行校准；采用本文提出的方法校准后，响应电流的数字量如5所示，三相响应电流基本对称，可以保证电机的位置检测和换相的准确度。

测得的三相电感数字量如图6所示，可见三相电感基本对称。将数字量折合为实际值，最大电感0.89mH，最小电感0.15 mH；用LCR电桥测得的最大电感0.88mH、最小电感0.145mH，检测误差不超过2%，证明数字检测有足够的精度。

检测到转子位置角与实际位置角如图7所示，位置误差如图8所示。在一个机械周期内，平均位置检测误差为0.2775°机械角，最大的位置检测误差为0.8950°机械角。可见，本文检测方法具有较高的检测精度。

图6 三相电感数字量

图7 转子位置角

图8 转子位置角检测误差

4 结 论

开关磁阻电机的无位置传感器控制系统中，初始位置的检测十分重要，但是现有的方法很难检测开关磁阻电机的精确位置，本文在高频脉冲注入法的基础上，提出了一种精确检测转子初始位置的方法。根据开关磁阻电机的电感特性，将一个通电周期平均分为6个扇区；在电机静止时，同时向三相绕组注入一定频率的高频脉冲，根据三相绕组对注入脉冲的响应电流的峰值大小，判断转子所处扇区；任一扇区中，三相绕组的电感曲线各不相同，位于中间位置的一相电感曲线接近直线，由于三相绕组的对称性，6个扇区的直线段顶点的电感相等。通过单相或两相绕组通电，使转子定位于任一在扇区的两个顶点处，预先测出两个顶点位置的电感；通过线性插值的方法，可准确计算任一扇内任意一点的位置。考虑到电流传感器和运算放大器存在零点漂移和增益误差，为提高检测精度，必须对响应电流峰值进行校准，通过线性校准，保证了检测到的三相响应电流和电感对称性。

本文提出的初始位置检测方法应用于一台4kW、60Vdc、3000r/min的三相12/8极开关磁阻电机，测试结果显示：在一个机械周期内，平均位置检测误差为0.2775°机械角，最大的位置检测误差为0.8950°机械角，证明所提方法具有较高的位置检测精度。