增进数学体验,提升数学素养
单红霞
数学体验就是学生亲历教学情境、参与数学活动的过程.通过数学体验,可以让学生获得知识的领悟、情感的体验,从而完善自身的知识建构,促进经验的生长.数学教学要紧贴学生的生活,基于学生的视角去观察,了解他们在学习中存在的困难,分析问题产生的原因,因学而教,只有这样才能满足学生的求知需要.如何增进学生的数学体验,促进学生的深度思考呢?笔者结合自身的教学实践,谈一些看法.
一、创设教学情境,促进直觉体验
数学教学要融入学生的生活,让学生从常见的事物中探究数学知识,从而促进他们对问题的理解.教师要创设真实的情境,能通过实物呈现的就不用文字叙述,能动手操作的不能依赖于媒体的呈现,从而让学生获得直接的体验.
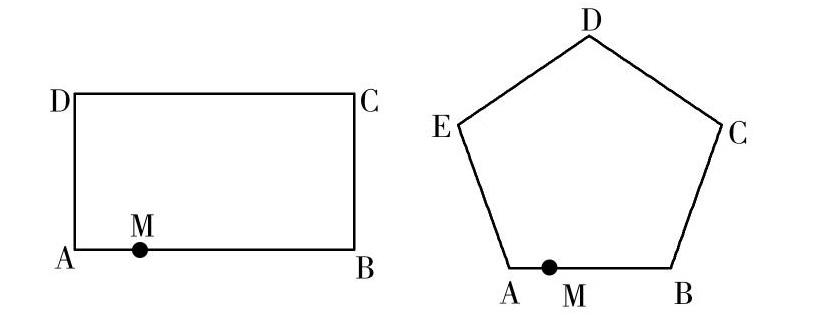
如在《多边形的内角和与外角和》一课的教学中,我营造了林林与芳芳分别从矩形、正五边形的广场绕一圈的情境,让学生说说他们的身体分别转过了哪些角.林林沿矩形转过1圈后,他轉过的角度的和是多少?芳芳在点M处沿五边形的广场周围的道路步行,从一条道路转到下一条道路,身体转动的角是哪些角,你能在五边形中把它们表示出来吗?度量这些角,你发现了什么?通过这种生活化情景的创设,学生很容易被带入其中,从而有助于学生对多边形的内角和与外角和有深入的理解.
二、设置启发问题,促进抽象体验
数学学习的过程也是解决问题的过程,教师的提问不能满足于是非问、描述问,而是要以问引发学生的探索欲望.问题的提出是多种多样的,教师要在知识的关键点、转折处提问,以引发学生的认知冲突,促进学生的深入思考.教师要基于学生已有的生活经验设计问题串,这样可以促进概念的引入,帮助学生建构知识体系.当然,问题串要具有梯度,有一定的层次性.此外,教师还可以借悬念内容“吊住”学生的胃口,让学生对后续的知识充满兴趣,对学习充满期待.总之,教师要引领学生探索数学概念的本质,促进学生产生认知冲突,引发学生的求知欲望.
三、增加实验环节,促进探究体验
教师要借助于数学实验让学生去感受、体验数学,让学生去发现、归纳,实现生活与数学的连接,促进学生的思考,体验数学的应用价值.数学实验能促进知行合一,让学生在“做”中实现知识的自主建构.实验工具是多种多样的,学生可以用量角器、尺规以及生活中的实物作为器材,可以通过摸球游戏探索概率,通过拼图游戏探索整式乘法与因式分解之间的关系.例如,在《多边形的内角和与外角和》一课的教学中,我先让学生随手画了一个三角形,并用量角器量出各个内角的度数,求出它们的和,再让学生将这个三角形的三个内角剪下来,然后将它们拼在一起,看看能获得什么结论.这样做可以为学生留出思索的空间,让学生分析三角形三个内角之间存在的数量关系,从而深入理解教材.
教师还要将信息技术与课程内容结合起来,通过几何画板等软件的操作,让每一位学生都有动手实践的机会,获得充分的数学经验.例如,教师可以利用Excel软件制作解二元一次方程组的计算器,学生只须输入相关的系数就能获得计算结果.在此过程中教师要提出问题串:该计算器有何缺陷?你能找到问题产生的原因是什么?二元一次方程组的解可能有什么特殊情况?你能完善该计算器吗?让学生思考这些问题,并鼓励和引导学生试着写出解三元一次方程组的计算器的设计方案.
四、及时检测评价,促进反思体验
在上完一节课后,教师往往只是通过让学生说说“这节课获得了哪些收获”“还有哪些疑问”来获得反馈,这样是远远不够的.课后练习能让学生及时消化知识,所以教师要通过随堂检测、课堂小结帮助学生回顾内容,促进知识的内化.如可以让学生通过拼图的方式理解a2-b2.具体操作是,让学生从一个大正方体中挖掉一个小正方形,将剩下的图形分割成面积分别为a(a-b)、b(a-b)的两个图形,这样学生就可以借助于图形理解a2-b2=a(a-b)+b(a-b)=(a+b)(a-b)了.当然,学生也可以从二维迁移到三维,借助图形理解立方差的因式分解.
总之,在初中数学教学中,教师要善于“让学”,为学生留有探索、体验的空间,通过有效的活动丰富学生的体验,促进学生的自主建构,引发学生的深度思考,从而促进学生数学素养的形成.

