平面向量要点导学

■刘 彬

平面向量是新课标高考命题的热点之一，这类命题新颖而精巧，解题方法灵活多样，既可以单独命题又可以与其他知识综合考查。那么在学习平面向量时，我们需要抓住哪些重点呢?

一、平面向量的有关概念

平面向量的有关概念包括向量本身的定义、零向量、单位向量、相等向量和共线(平行)向量等概念，还包含向量的夹角和一个向量在另一个向量方向上的投影等。

例1已知△A B C是边长为2的等边三角形，向量a，b满足则下列结论正确的是____。(写出所有正确结论的序号)

①a为单位向量；②b为单位向量；

解：因为等边三角形A B C的边长为2，可知①正确。因为，所以，即可知②错误，④正确。由于，所以a与b的夹角为120°，可知③错误。由，可知⑤正确。答案为①④⑤。

友情提示：相等向量具有传递性，非零向量的平行也具有传递性；共线向量即为平行向量，它们均与起点无关；向量可以平移，平移后的向量与原向量是相等向量。非零向量a与的关系：向量是与向量a同方向的单位向量。

二、平面向量的基本定理

平面向量基本定理：如果e1，e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1，λ2，使得a=λ1e1+λ2e2。在高考中，主要考查对这个定理的理解和应用。

例2在△A B C中，A B边的高为C D，若，且

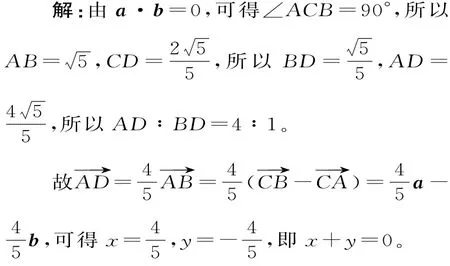
友情提示：解答本题的关键是确定∠A C B=90°，并能运用向量的加减法进行相互转化。

三、三点共线问题

三点共线问题，主要考查共线向量定理的灵活应用。

例3经过△O A B的重心G的直线与O A，O B分别交于点P，Q(图略)，设的值为____。

解：设由题意可知，

由P，G，Q三点共线，可知存在实数λ，使得，于是可得消去λ可

友情提示：若向量a，b共线，则存在不全为零的实数λ1，λ2，使得λ1a+λ2b=0成立；若λ1a+λ2b=0，当且仅当λ1=λ2=0时成立，则向量a，b不共线。