本期试卷参考答案
编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!

平面向量综合演练A卷参考答案与提示
一、选择题
1.提示:应选C。
2.提示:应选C。
3.提示:(数形结合法)以A为坐标原点,A B,A D所在直线为x,y轴,建立直角坐标系。点M所在区域可表示为(x-1)2+(y-1)2≤1(0≤x≤2,0≤y≤2)。设点M(x,y)。由A(0,0),B(2,0),可得1)2+y2-1。易得(x-1)2+y2≤2y∈[0,4],故应选C。
4.提示:应选D。
5.提示:应选B。
6.提 示 :,所以A D∥B C,且A D≠B C,可知四边形A B C D是梯形。应选C。
7.提示:应选D。
8.提示:应选 A。
9.提示:应选D。
10.提 示,显然的长度为半个周期。由周期=2,可得|,故所求值为2。应选D。
11.提 示 :由。设与的夹角为α,由,可得,所以=1。以A为坐标原点,A D为x轴,A B为y轴,建立平面直角坐标系(图略),则B(0,3),因 此应选C。
12.提示:设B C的中点为M,则,也即,可知P,M,A三点共线,且P是AM上靠近A点的一个三等分点。应选B。
13.提示:应选A。
14.提示:应选A。
15.提示:应选C。
16.提示:应选B。
17.提示:应选C。
二、填空题
18.提示:答案为②。
19.提示:答案为①②③④⑤。
20.提示:设P(x,y)。由易得2x-y+5≤0。由解得点A(-5,-5)或B(1,7)。由2x-y+5≤0得点P在圆左边弧A B上,结合限制条件,可得
21.提示:答案为①③。
22.提示:若每个向量的方向相同,模相等,则无极大向量,①不正确。由题意得a,b,c围成闭合三角形,则任意向量的模等于除它本身外所有向量和的模,②正确。3个向量都是极大向量,等价于3个向量之和为0,故W1={a1,a2,a3},W2={b1,b2,b3}中的每个元素都是极大向量时,W1∪W2中的每一个元素也都是极大向量,③正确。答案为②③。
23.提示
24.提示:m=1。
25.提示:根据题意可得,,所以()·(k2∈Za⊗bb。因为所以因为k1,k2∈Z,所以因为|a|≥|b|,所以k1=2,k2=1,所以a⊗b,故
26.提示:由,可知?以B为坐标原点,分别以B A,B C所在的直线为x轴,y轴,建立平面直角坐标系(图略)。由题意可得B(0,0),A(1,0),C(0,2)。设D(x,y),则2-y)。由,可得,所以点D在以为圆心,半径的圆上。因为表示B,D两点间的距离,而所以的最大值为
27.提示:因为所以注意到,可得所以,解得
28.提示:由题设可知A B=B C=BN=1。因为点M在以A B为直径的半圆上,所以AM⊥BM。又BM⊥BN,所以AM∥BN,所以因为AM⊥BM,A B=1,所以,所以。于是可得<1,所以当时,可得的最大值为
29.提示的值为
30.提示:λ=-4。
31.提示:因 为所以,所以。因为A B∥C D,C D=,所以可 得
32.提示:由,可得0,可得,即B A⊥A C。以点A为原点,A B为x轴,建立直角坐标系x A y(图略),则B(6,0),C(0,3)。设P(x,y),可得10],所以 当x=2,y=1 时有最小值,此时
三、解答题
33.提示:(1)由已知得(2e1-e2)-(e1+3e2)=e1-4e2。因为,所 以又与有公共点B,所以A,B,D三点共线。
(2)k=12。
34.提示:(1)因为(2a-3b)·(2a+b)=61,所以4|a|2-4a·b-3|b|2=61。又|a|=4,|b|=3,所以64-4a·b-27=61,即a·b=-6,所以。因为0≤θ≤π,所以
(2)|a+b|2=(a+b)2=|a|2+2a·b+|b|2=13,所以
35.提示:(1)由题意知。由
因为a与b不共线,由平面向量基本定理可得解得
36.提示:(1)因为a=(cosx,sinx),b=,所以
若cosx=0,则sinx=0,与sin2x+cos2x=1矛盾,故cosx≠0。于是可得tanx又x∈[0,π],所以
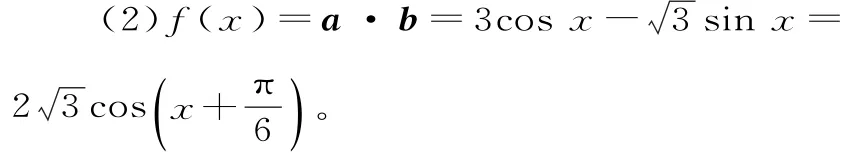
因为x∈[0,π],所以所以
三角恒等变换综合演练B卷参考答案与提示
一、选择题
1.提示:应选B。
2.提示:应选D。
3.提示:对于 A ,cos14°+sin14°=2sin(60°+14°)=2sin 74°。对于B,cos 24°+sin 24°=2sin(60°+24°)=2sin 84°。对于C,cos64°+sin64°=2sin(60°+64°)=2sin 124°=2sin56°。对于 D ,cos74°+sin 74°=2sin(60°+74°)=2sin134°=2sin 46°。应选D。
4.提示:应选C。
5.提示:应选B。
6.提示:应选C。
7.提示:应选A。
8.提示:应选D。
9.提示:应选A。
10.提示:应选C。
11.提示:应选C。
12.提示:应选A。
13.提示:应选C。
14.提示:应选C。
二、填空题
15.提示:原式=2。
16.提示:依题意可得大,小正方形的边长分别是5,1,于是可得5sinθ-5 cosθ=1,即,所以(sinθ+因此故
17.提示:原式
18.提示:因为x=2 π是一条对称轴,所以又f(x)在区间上单调,所以可得,所以ω的取值集合为
19.提示
20.提示
21.提示
22.提示
23.提示:f(x)=(sinx+cosx)2+sinx+cosx-1,令sinx+cosx=t,则由可得,即得。原函数可化为由函数g(t)=t2+t-1的图像开口向上,其对称轴方程为t=,可得当0≤t≤时,g(t)单调递增。当t=0时,g(t)取得最小值-1,即函数f(x)的最小值为-1。
24.提示:由题意可得,即因为,且所以0,即,所以。故
25.提示:对任意实数x,恒有f(α1)≤f(x)≤f(α2),则f(α1)为最小值,f(α2)为最大值。因为,而-1≤sinx≤1,所以当sinx=-1时,f(x)取得最小值;当时,f(x)取得最大值。所以。所以cosα=0。1故cos(α1-α2)=cosα1cosα2+sinα1sinα2=
26.提示
27.提示
28.提示:由可得。故 t a n(α+)=β。由可得,所
29.提示
30.提示
三、解答题
31.提示:(1)函数f(x)的定义域是{x|x
因为β∈(0,π),所以由,可得,即由,可得,即β=。故或
32.提示
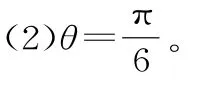
33.提示:(1)函数f(x)的单调递减区间为
34.提示:(1)由题意可得由f(x)的图像关于直线x=π 6对称,可得且ω∈[0,3],解得ω=1。由,解得故函数f(x)的单调递增区间为
35.提示:(1)函数f(x)的最小正周期为π。函数f(x)在上的最大值为2,最小值为
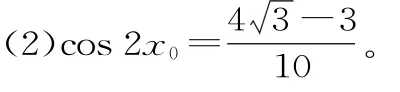
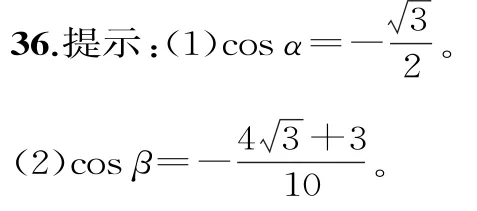
37.提示:(1)由题设可得由易得
38.提示:(1)函数f(x)的单调递增区间为
39.提示:(1)由题意可得f(x)=。由可得。因为a>0,所以a的最小值为
——外撇柴

