三角恒等变换常见典型考题赏析
■尹志雄
作者单位:江苏省扬州市宝应县曹甸高级中学
题型1:三角函数公式的变形应用
三角函数公式变形应用需注意的两个问题:①公式逆用时,一定要注意公式成立的条件和角之间的关系;②注意特殊角的应用,当式子中出现等数值时,一定要考虑引入特殊角。要熟记三角函数公式的变式,如sinαsinβ+cos(α+β)=cosαcosβ,cosαsinβ+sin(α-β)=sinαcosβ,tanα±tanβ=tan(α±β)·(1∓tanαtanβ),cos2α=
例1 已知sin 76°cos46°-cos76°sin46°,则 sinα=( )。
解:由tanα=sin76°cos 46°-cos 76°·,且α∈,可得由上容易得到应选A。
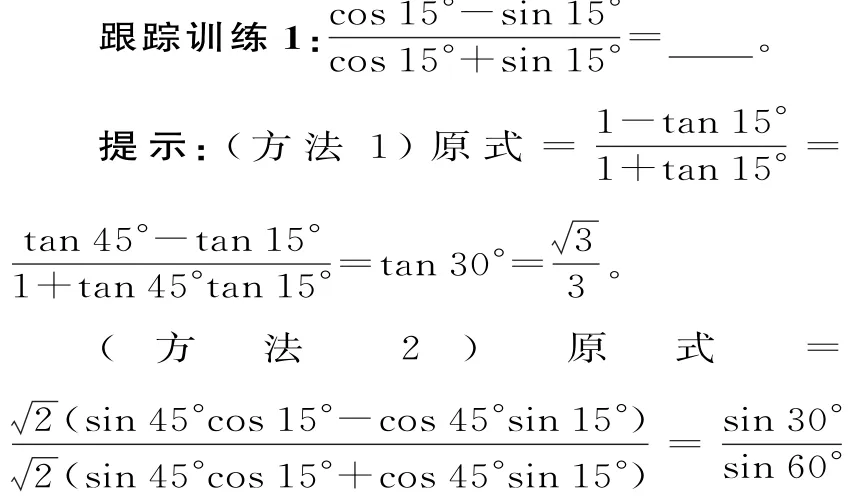

题型2:角的变换
熟练掌握常用的角变换技巧,如α=(α+β)-β=(α-β)+β,2α=(α+β)+(α-β),
例2 设α为锐角,若,则的值为( )。

解:(方法1)因为α为锐角,所以。因为所以。应选B。

(方法2)因为α为锐角,所以又因为所以

跟踪训练2:已知则的值是( )。

提示:由,可得
题型3:三角函数的图像与性质问题
求解三角函数的奇偶性、周期性、单调性、最值等问题时,一般先要进行三角恒等变换,把三角函数式化为一个角的一种三角函数,再根据三角函数的奇偶性以及周期公式求解。解答这类问题的关键是熟练掌握三角函数图像的应用。
例3 已知函数若将函数f(x)的图像向左平移个单位长度,得到函数g(x)的图像,则函数g(x)在区间]上的最大值和最小值之和为( )。

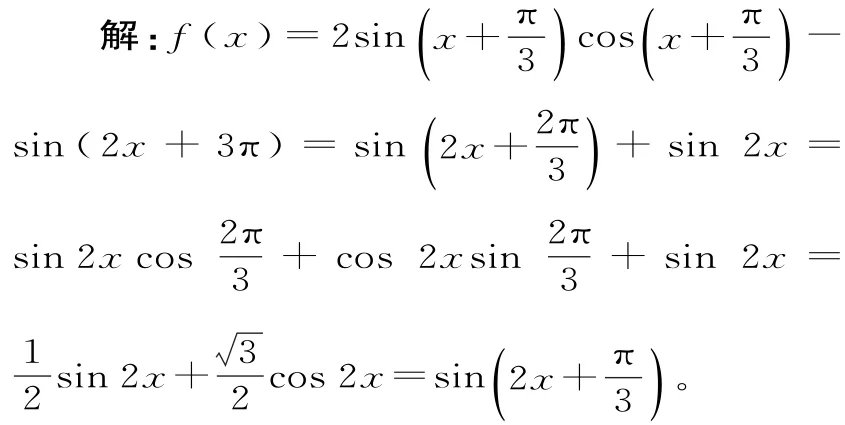
由题意可知函数g(x)=由,可得,可知当,即时,函数g(x)取得最小值,且g(x)min=-1;当,即x=0时,函数g(x)取得最大值,且故函数g(x)在区间上的最大值和最小值之和为应选A。
跟踪训练3:已知函数+θ)-cos(2x+θ)(-π<θ<0)的图像关于点对称,记f(x)在区间上的最大值为n,且f(x)在[mπ,nπ](m<n)上单调递增,则实数m的最小值是____。
提示:因为的图像关于点对称,所以0。又因为-π<θ<0,所以,即θ=,这时当x∈即n=2。令当k=2时,即实数m的最小值是
题型4:非特殊角的求值问题
解答这类问题,要观察所给角与特殊角间的关系,利用三角变换转化为求特殊角的三角函数值的问题。此类问题也可通过代数变形(如正负项相消、分子分母相约)的方式来求值。

题型5:给值求值问题
给值求值问题的关键是找出已知式与待求式之间的联系及函数的差异,一般可以适当变换已知式,求得另外某些函数式的值,以备应用,同时要注意变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的。
例5 已知的值。
解:因为,且2sin2α-sinα·cosα-3 cos2α=0,则(2sinα-3 cosα)(sinα+cosα)=0(sinα+cosα≠0),所以2sinα=3 cosα。又sin2α+cos2α=1,所以cosα=。故原式=
跟踪训练5:已知sin(α-β)cosα-cos(β,其中β是第三象限角,则
提示:依题意可将已知条件变形为,可得sinβ=
因为β是第三象限角,所以cosβ=
题型6:三角函数的求角问题
这类问题的一般解题思路是:已知正切函数值,选正切函数,已知正弦或余弦函数值,选正弦或余弦函数。若角的范围是,选正弦或余弦函数皆可;若角的范围是(0,π),选余弦函数较好;若角的范围为,选正弦函数较好。例6 已知A,B均为钝角,且,则A+B=____。解:因为,解得又因为A为钝角,所以cosA=由,且B为钝角,可得cosB=
故cos(A+B)=cosAcosB-sinA·。又A,B均为钝角,则A,B∈,所以A+B∈(π,2 π),由此可得A+
跟踪训练6:已知α,β∈(0,π),且tan(α,则2α-β的值为____。
提示:由tanα=tan[(α-β)+β]=,可得由,可得0<2α<。由,可得,所以-π<2α-β<0。因为tan(2α-β)=,故
题型7:三角函数与平面向量的交汇
平面向量与三角函数在“角”之间存在着密切的联系。如果在平面向量与三角函数的交汇处设计命题,其形式多样,解法灵活,且极富思维性和挑战性。对于这类问题,根据所给三角式的结构及向量间的相互关系进行处理,可使解题过程得到简化,从而提高解题的效率。
例7 已知向量a=(cos 2α,sinα),b=
解:由a=(cos 2α,sinα),b=(1,2sinα,且a·,可得cos 2α,即cos 2α+2sin2α-也即cos 2α+1-cos 2α-sinα=,所以可得
跟踪训练7:已知向量a=(cosθ,sinθ),向量则|2a-b|的最大值与最小值的和为____。
提示:由题意可得a·b=cosθ-sinθ,则∈[0,4],故|2a-b|的最大值与最小值的和为4。
题型8:三角函数中的新定义问题
近年来的高考试题相继推出了以能力立意为目标,以增大思维容量为特色,具有相当浓度和明确导向的创新题型。这类创新题型大多以新定义问题的形式出现,值得同学们重视。新定义问题主要是指即时定义新概念、新公式、新定理、新法则、新运算,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新定义,这样有助于对新定义的透彻理解。
例8 已知下凸函数f(x)在定义域内满足不等式若函数y=tanx在上是下凸函数,那么在锐角△A B C中,求tanA+tanB+tanC的最小值。
解:因为y=tanx在上是下凸函数,所以(tanA+tanB+tanC)≥,即tanA+,当且仅当tanA=tanB=tanC,即时等号成立,所以tanA+tanB+tanC的最小值为
跟踪训练8:已知函数y=f(x)(x∈R),对函数y=g(x)(x∈I),定义g(x)关于f(x)的“对称函数”为y=h(x)(x∈I),y=h(x)满足:对任意x∈I,两个点(x,h(x)),(x,g(x))关于点(x,f(x))对称。若h(x)=-asinx是g(x)关于f(x)=的“对称函数”,且g(x)在上是减函数,则实数a的取值范围是____。
提示:根据对称函数的概念,可知h(x)+g(x)=2f(x),即g(x)=2f(x)-h(x)+1。令则函数+1,其对称轴方程为,且图像的开口向下。由于函数g(x)在上 递 减 ,t=sinx在上递增,根据复合函数的单调性可,即a≤2,故实数a的取值范围为(-∞,2]。
题型9:三角函数中的恒成立问题
三角函数中的恒成立问题通常含有参数,解答这类问题,一定要注意三角函数自身的有界性,结合自变量的取值范围,才能正确求解。
例9 已知不等式对于x∈恒成立,则实数m的取值范围是____
解:因为所以原不等式等价于m≤在上恒成立。因为所以,由此可得m≤
,即实数
跟踪训练9:已知函数f(x)=,若对任意的实数α∈,都存在唯一的实数β∈[0,m],使f(α)+f(β)=0恒成立,则实数m的最大值是____。
提示:已知函数,若对任意的实数,则要使f(α)+f(β)=0 恒 成立,需满 足f(β)∈,即,所以0≤,可得故实数m的最大值是

