品味三角恒等变换中的误区警示
■樊炯炯
三角恒等变换的方法灵活多变,突出对思维的灵活性和严密性的考查,解题时稍有不慎,便会出现增解、漏解甚至错解的情况。本文归纳三角恒等变换求解中的误区,希望能给同学们以警示。
误区1:三角函数定义理解出错
例1 已知角θ的终边落在直线y=-3x上,求2sinθ+3 cosθ的值。
错解:取直线上一点(1,-3),则sinθ=-3,cosθ=1,所以2sinθ+3 cosθ=-3。
剖析:上述解法对sinθ=y,cosθ=x的理解有误,定义中的(x,y)必须是角θ终边与单位圆的交点坐标,不是任意点。
正解:设角θ终边与单位圆的交点为(x,y),则由此解得或故
警示:此类问题需要借助单位圆,将角θ终边上的点转化成终边与单位圆的交点,通过解方程组求得交点,再依据三角函数的定义求解。
误区2:应用诱导公式忽视分类意识

错解:原 式
剖析:上述解法对三角函数诱导公式理解不准确,没有对整数k分奇偶性进行讨论。

警示:诱导公式(k∈Z)的本质是:奇变偶不变(对k而言,指k取奇数或偶数),符号看象限(把α看成锐角时整体角所在的象限)。当整体角无法确定象限时,一定要对整数k分奇偶性进行讨论。
误区3:对诱导公式中的符号看象限理解不正确
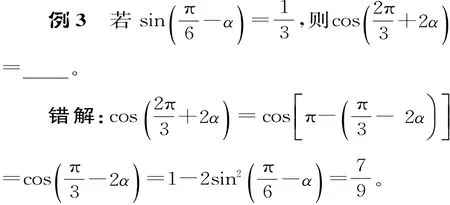
剖析:上述解法对中的符号看象限理解不正确。
正解:利用诱导公式可把看成锐角,则是第二象限角,所以
警示:诱导公式可简记为:奇变偶不变,符号看象限。这里的“奇偶”指的是的倍数的奇偶,“变与不变”指的是三角函数名称的变化。“符号看象限”的含义是:把整个角看成锐角时,所在象限的相应余弦函数值的符号。
误区4:给值求角中选用三角函数名称不当致错
例4 若,且α,β均为锐角,求2α+2β的值。
错解:因为α为锐角,所以cosα=又β为锐角,所以cosβ。所以sin(α+β)=。由于0°<α<90°,0°<β<90°,所以0°<α+β<180°,所以α+β=45°或α+β=135°,即2α+2β=90°或2α+2β=270°。
剖析:因为y=sinx在(0,π)上不是单调函数,y=cosx在(0,π)上是单调函数,所以应求cos(α+β)的值,可避免出错。
正解:因为α为锐角,所以cosα=。又β为锐角,所以cosβ所以cos(α+β)=
由于0°<α<90°,0°<β<90°,所以0°<α+β<180°,故α+β=45°,可得2α+2β=90°。
警示:由三角函数值确定角的大小,一定要注意结合角的范围选择合适的三角函数。已知正切函数值,选正切函数;已知正、余弦函数值,若角在(0,π)内,选余弦函数,若角在内,选正弦函数。
误区5:忽视隐含条件的挖掘致错
例5 若α,β,γ均为锐角,且sinα+sinγ=sinβ,cosβ+cosγ=cosα,则α-β=____。又α,β均为锐角,所以
错解:由条件可得sinα-sinβ=-sinγ,cosα-cosβ=cosγ,两式平方相加得cos(α
剖析:上述解法没有真正利用α,β,γ均为锐角的条件,从而导致多解。
正解:由条件可得sinα-sinβ=-sinγ,cosα-cosβ=cosγ,两式平方相加得cos(α。由γ为锐角,可得sinα-sinβ=
因为α,β均为锐角,所以α<β,则β<0,故-sinγ<0,因此条件中隐含着sinα<sinβ。
警示:当三个角均为锐角时,一定要挖掘它们之间的隐含条件,如题中由sinα-sinβ=-sinγ<0,可得α<β。
感悟与提高
已知sinθ,cosθ是方程4x2-4m x+2m-1=0的两个实根,且,则m=____。
提示:由根与系数的关系可知1+2sinθcosθ后可解得

