三角恒等变换中的创新问题

■王 飞 刘大鸣(特级教师)

高考对三角恒等变换主要是围绕“角的变换、名称的变换、公式的变换、结构的变换以及常数的变换”等展开的，体现目标意识下的“特殊值、消项和约项”，彰显函数与方程思想、转化与化归思想以及数形结合思想的具体应用。本文主要介绍这类创新问题中的求解策略。

创新1：姊妹关系式中的平方法和方程组观念的应用

例1 已知α为第二象限角，sinα+，则间的关系，对两边平方可得

解：注意同角关系中的平方与二倍角之

因为α是第二象限角，可得sinα＞0，cosα＜0，即cosα-sinα＜0，所以cosα-

故 cos2α=cos2α-sin2α=(cosα+

评析：解答本题的关键是利用sinα+cosα、sinα-cosα和sinαcosα三姊妹关系式，借助sin2α+cos2α=1和sin 2α=2sinα·cosα的合理应用求解的。解题时，要注意函数值对角的限制作用，应尽量缩小角的取值范围可避免多解。

创新2：三角恒等变换中的差异分析法

解：通过差异分析，利用平方差公式分解因式，逆用和差角公式，通过“降次消项”求值。

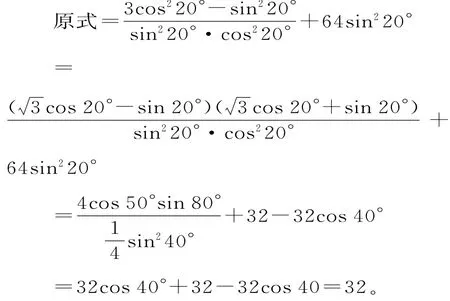
评析：通过观察角、函数名称以及运算结构之间的关系，进行差异分析，促使差异的转化。题中通过sin(α±β)=sinαcosβ±cosα·sinβ，cos(α±β)=cosαcosβ∓sinαsinβ和sin 2α=2sinαcosα的逆用，促使分子、分母约分，再 利 用降次消项求值。

创新3：三角恒等变换中的换元变角法

例3 设α为锐角，若则

的值为____。

解：把所求角用已知角和特殊角表示，采用换元变角法求解。

评析：换元变角法的实质就是角的配凑，如，其中就是题中的新元x，即

创新4：三角函数名称的互化(切弦互化)

解：利用切化弦和逆用倍角公式，通过约分求值。

评析：本题凸显目标意识下的“化异为同与分式约项”。解题时，要熟练运用切化弦和变角(20°=30°-10°)等技巧，同时还要灵活运用二倍角公式、和差角公式。

创新5：三角函数结构式的变换

例5则的值是____。

解：注意到所求式2θ是关于sinθ，cosθ的二次齐次式，可改变结构化为关于tanθ的齐次式求解。由已知可得3sinθ-cosθ=0，所以

评析：对已知式的结构特征进行变形，使其更贴近某个公式或期待的目标，这是三角结构式变换的宗旨。常见的三角结构式的变换有“升幂与降幂”“常值代换”“逆用与变用公式”“通分与约分”“分解与组合”。

创新6：存在性问题中的三角恒等变换

例6 已知函数f(x)=cos2x+cos2(x+α)+cos2(x+β)，其中α，β为常数，且满足0≤α＜β≤π。对于任意实数x，问是否存在α，β，使得f(x)是与x无关的定值。若存在，求出α，β的值；若不存在，请说明理由。

解：在假设存在的条件下，利用倍角公式改变结构特征，借助f(x)是与x无关的定值构建方程组求解。

假设存在α，β满足条件，则函数f(x)=。由此可知f(x)为定值的条件是消去2β可得(1+cos 2α)2+sin22α=1，解得cos 2α，所以。因为0≤α＜β≤π，故存在使得f(x)为定值。

评析：在假设存在的条件下，把握函数f(x)是与x无关的特征，利用三角公式化简函数式，构建方程组求值，这是存在性问题常用的思维方法。

创新7：与向量交汇中的三角恒等变换

例7 已知向量m=，且f(x)=m·n+1。

(1)设方程f(x)-1=0在(0，π)上有两个零点x1，x2，求f(x1+x2)的值。

(2)若把函数y=f(x)的图像向左平移个单位，再向上平移2个单位，得到函数g(x)图像，求函数g(x)在上的单调增区间。

解：(1)由题意可得函数f(x)=

由f(x)-1=0，可得。由x∈(0，π)，且两个零点为x，x，12利用对称性可得，所以

评析：利用向量数量积的运算，借助余弦函数在区间上的对称性简化求值，利用整体变量观念解出单调区间，凸显三角函数的工具性、应用性及交汇性。

创新8：函数最值求解中的三角换元法

例8 求函数的最值。

解：注意变量的取值范围，挖掘隐含关系，利用三角换元法求解。

由题意可得-2≤t≤6。

由t的有界性，可考虑三角换元法，即设由此可得函数

umin是φ(0)和中的较小者，因为

评析：当自变量取值为区间时，可“设角换元”，题中要关注自变量对角的限制要求，其目的是便于进一步利用三角函数的有界性求解。

感悟与提高

提示：设A=α+β+γ，B=α-β+γ，则2(α+γ)=A+B，2β=A-B。因 为sin[2(α+γ)]=3sin2β，所以sin(A+B)=3sin(A-B)，即sinAcosB+cosAsinB=3(sinAcosB-cosAsinB)，2 cosAsinB=sinAcosB，由此可得tanA=2 tanB。故。应选D。