构建几何模型巧解函数最值问题

四川省成都市四川师范大学附属中学(610061) 康 琳

一、构建三角形模型

例1(2013年高考全国卷Ⅰ)若函数的图像关于直线x=−2对称,则f(x)的最大值是____.

解观察函数结构,发现x=±1是函数f(x)的两个零点,由函数图像关于直线x=−2对称得,x=−3,x=−5是函数f(x)的两个零点,即x=−3,x=−5是二次方程x2+ax+b=0的两个根,由韦达定理可得a=8,b=15.f(x)=(1−x)(x+1)(x+3)(x+5),观察结构发现可以和海伦公式联系起来.由函数图像可知,f(x)取最大值时的x,x∈(−5,−3)或x∈(−1,1).不妨设x∈(−1,1),则 1−x,x+1,x+3,x+5均大于零,由(1−x)+(x+1)+(x+3)+(x+5)=2x+10=2p,所以p=x+5,得a=2,b=4,c=2x+4,因为x∈(−1,1),所以 2x+4∈(2,6),构造 ∆ABC,∠ACB∈(0,π),BC=2,AC=4,易知当时,S取最∆ABC大值所以f(x)的最大值16.

评注这里借助了四项连乘的形式与海伦公式联系,在满足四项均为正的条件下,构造三角形模型,利用几何关系求最值[1].

二、构建距离模型

例2求的最小值.

解设函数上任意一点函数f(x)=lnx,x＞0上任意一点N(a,lna),则原表达式构建的几何模型是点点距离|MN|与点M到x轴距离的和,设抛物线的焦点是F(0,1),由抛物线定义可得,即求|MN|+|FM|−1的最小值.

如图1所示,当M,F,N共线且FM与函数f(x)在点N处的切线垂直时取得|MN|+|FM|−1的最小值,设N(x0,lnx0),切线斜率解得x=01,即|MN|+|FN|−1的最小值

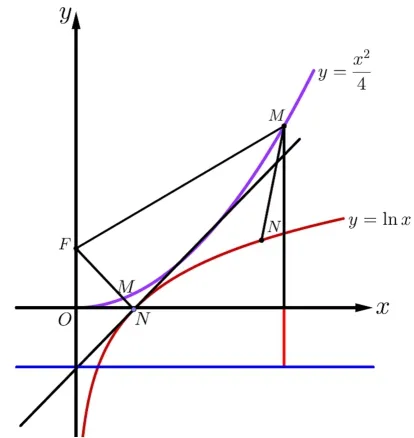
图1

评注被开方式的最高次数为2时,可以考虑构建两点之间的距离这个几何模型,构造几何图形求函数最值可以使运算量大大减小,在教学中我们要重视求最值的方法的训练和提炼,但无须追求灵巧新奇,以常见的基本方法为主,相信熟能生巧,基本功扎实了,自然能够得心应手[2].

三、构建圆模型

例3(2018年高考全国卷Ⅰ)已知函数f(x)=2sinx+sin2x,则f(x)的最小值是___.

解f(x)=2sinx(1+cosx),设a=1+cosx,b=sinx,则(a−1)2+b2=1,A(a,b)是圆上任意一点,它关于x轴的对称点B(a,−b),2ab的最小值即为以O为顶点的等腰∆OAB的面积最大值两倍的相反数.易得当∆OAB是等边三角形时,取得面积的最大值,1是其外接圆半径,所以f(x)的最小值是

评注通过双换元后,新的未知元满足二次式的结构,考虑构建圆模型,数形结合将函数的最值转化为三角形面积的最值.

四、构建椭圆模型

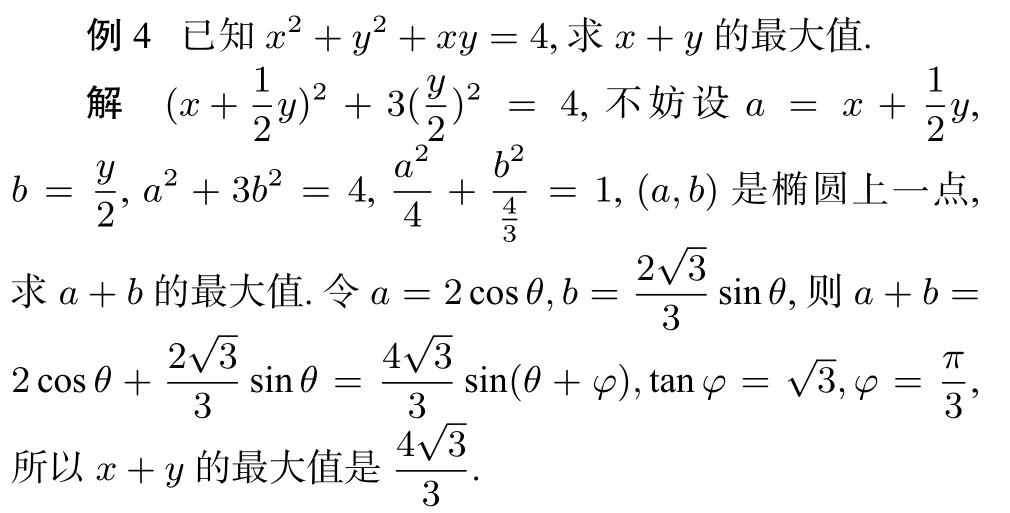
评注双换元后,变元满足的等量关系是椭圆方程,再用参数方程换元,转化为函数研究最值[3];不管是用几何法还是代数方法,或兼用两种方法来描述,取决于哪种方法更加优美,更加简单,或更便于学生接受.

五、构建双曲线模型

例5求函数的最小值.

解令动点(µ,ν)的轨迹是双曲线在第一象限(包括轴上一顶点)的部分,原命题转化为求µ−ν的最小值,当平行直线与一象限的双曲线相切时,取得最小值,易得f(x)的最小值为

评注二次式可以构建三角形模型或者是二次曲线模型,体现了数形结合方法的重要作用,它一方面体现了数的严谨性,另一方面又体现了形的直观性[4].

六、构建抛物线模型

例6求函数的最大值.

解令则有y2=4(x−1),(x≥1,y≥0),动点(x,y)的轨迹是抛物线在第一象限(包括顶点)的部分,由抛物线的参数方程原命题转化为求y−x=−4t2+4t−1的最大值,易得f(x)的最大值为0.

评注根式换元后,得到含二次式和一次式的结构,构建抛物线模型.

小结在解决问题过程中,对式子结构的认识、分析,或经过换元后结构的再认识、分析,构建特殊的几何模型,代数问题几何化,能提供更开阔的解题思路[5].